А. Ряд Лорана
Функция 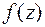 , однозначная и аналитическая в кольце
, однозначная и аналитическая в кольце  , представляется (единственным образом) в этом кольце сходящимся рядом Лорана
, представляется (единственным образом) в этом кольце сходящимся рядом Лорана
 . (1)
. (1)
Коэффициенты  вычисляются по формулам
вычисляются по формулам
 ,
,  (2)
(2)
где интегрирование производится по окружности 
 .
.
В замкнутом кольце  ряд Лорана сходится равномерно.
ряд Лорана сходится равномерно.
В частном случае при  область сходимости ряда Лорана есть круг с выколотым центром
область сходимости ряда Лорана есть круг с выколотым центром 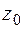 , при
, при  – это внешность круга
– это внешность круга  .
.
Разложение (1) можно разбить на две части:
 .
.
Ряд по положительным степеням  называется правильной частью ряда Лорана.
называется правильной частью ряда Лорана.
Ряд по отрицательным степеням  называется главной частью ряда Лорана
называется главной частью ряда Лорана
На внешней граничной окружности радиуса  имеется, по крайней мере, одна особая точка функции
имеется, по крайней мере, одна особая точка функции  , являющаяся суммой правильной части ряда Лорана, а на внутренней граничной окружности радиуса
, являющаяся суммой правильной части ряда Лорана, а на внутренней граничной окружности радиуса  имеется, по крайней мере, одна особая точка функции
имеется, по крайней мере, одна особая точка функции  , являющаяся суммой главной части ряда Лорана. Ряд Тейлора является частным случаем ряда Лорана.
, являющаяся суммой главной части ряда Лорана. Ряд Тейлора является частным случаем ряда Лорана.
Общие формулы (2) для определения лорановских коэффициентов обычно мало пригодны для вычислений. В некоторых случаях могут быть использованы готовые разложения элементарных функций в ряд Тейлора.
Пример 1. Разложить  в ряд Лорана при
в ряд Лорана при  .
.
 Решение. Функция
Решение. Функция  имеет две особые точки
имеет две особые точки  , которые получаем из условия
, которые получаем из условия  . Значит, имеются три области с круговыми границами с центром в точке
. Значит, имеются три области с круговыми границами с центром в точке  , в каждой из которых
, в каждой из которых  – аналитическая функция:
– аналитическая функция:  1) круг
1) круг 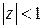 ; 2) кольцо
; 2) кольцо  ; 3) область
; 3) область  .
.
В этом примере легко получить лорановское разложение в каждой из областей, не прибегая к формулам (2) для вычисления коэффициентов. Представим заданную функцию в виде суммы элементарных дробей:
 .
.
Рассмотрим последовательно все случаи.
1.Разложение в круге 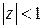 .
.
Функция  есть сумма бесконечной геометрической прогрессии:
есть сумма бесконечной геометрической прогрессии:
 . (3)
. (3)
Здесь знаменатель прогрессии  , ряд сходится при
, ряд сходится при  .
.
Функция  лишь постоянным множителем
лишь постоянным множителем  отличается от суммы бесконечной геометрической прогрессии со знаменателем
отличается от суммы бесконечной геометрической прогрессии со знаменателем  :
:
 . (4)
. (4)
Ряд, стоящий справа в (4), сходится при  , то есть в круге
, то есть в круге  (в частности он сходится в рассматриваемом круге
(в частности он сходится в рассматриваемом круге 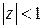 ).
).
Складывая (3) и (4), получаем:

Значит, в круге 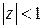 заданная функция представляется сходящимся рядом по положительным степеням
заданная функция представляется сходящимся рядом по положительным степеням  :
:
 , где
, где  ,
,  .
.
Естественно, для аналитической в круге 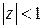 функции получили ряд Тейлора (отрицательные степени отсутствуют).
функции получили ряд Тейлора (отрицательные степени отсутствуют).
2. Разложение в кольце  . В этой области ряд (4), сходящийся при
. В этой области ряд (4), сходящийся при  , остается сходящимся. Но ряд (3), сходящийся в круге
, остается сходящимся. Но ряд (3), сходящийся в круге 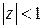 , вне этого круга, то есть в рассматриваемом кольце, расходится. Поэтому функцию
, вне этого круга, то есть в рассматриваемом кольце, расходится. Поэтому функцию  следует представить в виде
следует представить в виде  и рассмотреть дробь
и рассмотреть дробь  как сумму бесконечной геометрической прогрессии со знаменателем
как сумму бесконечной геометрической прогрессии со знаменателем  . Разложение (3) заменяется другим:
. Разложение (3) заменяется другим:
 . (5)
. (5)
Ряд, стоящий справа в (5), сходится, когда  , то есть при
, то есть при  (в частности, в рассматриваемом кольце). Складывая (5) и (4), получаем:
(в частности, в рассматриваемом кольце). Складывая (5) и (4), получаем:
 .
.
Значит, в кольце  заданная функция представляется сходящимся рядом Лорана:
заданная функция представляется сходящимся рядом Лорана:
 ,
,  .
.
3. Разложение в области  . Разложение (5), справедливое при
. Разложение (5), справедливое при  , сохраняется, если
, сохраняется, если  . Но для ряда (4) радиус сходимости равен 2, значит, этот ряд расходится в области
. Но для ряда (4) радиус сходимости равен 2, значит, этот ряд расходится в области  . Поэтому функцию
. Поэтому функцию  следует представить в виде
следует представить в виде  и рассмотреть дробь
и рассмотреть дробь  как сумму бесконечной геометрической прогрессии со знаменателем
как сумму бесконечной геометрической прогрессии со знаменателем  . Разложение (4) заменяется другим:
. Разложение (4) заменяется другим:
 . (6)
. (6)
Ряд, стоящий справа в (6), сходится, когда  , то есть при
, то есть при  . Складывая (5) и (6), получаем
. Складывая (5) и (6), получаем  .
.
Значит, в области  заданная функция представляется сходящимся рядом по отрицательным степеням
заданная функция представляется сходящимся рядом по отрицательным степеням  :
:
 ,
,  ☻
☻
Пример 2. Функцию  разложить в ряд Лорана при
разложить в ряд Лорана при  .
.
 Решение. В примере 1 эта функция была представлена как сумма
Решение. В примере 1 эта функция была представлена как сумма  . Второе слагаемое уже представляет собой один из членов лорановского разложения по степеням
. Второе слагаемое уже представляет собой один из членов лорановского разложения по степеням  :
:  . Остается разложить по степеням
. Остается разложить по степеням  слагаемое
слагаемое  . Имеются две области, в каждой из которых это слагаемое – аналитическая функция:
. Имеются две области, в каждой из которых это слагаемое – аналитическая функция:
1)круг  с выколотым центром
с выколотым центром  ;
;
2)внешность круга  .
.
Рассмотрим оба случая.
1. Разложение в области  . Выделим в знаменателе выражение
. Выделим в знаменателе выражение  :
:  . Получили прогрессию со знаменателем
. Получили прогрессию со знаменателем  :
:
 (7)
(7)
Ряд справа сходится, если  . Следовательно, в круге
. Следовательно, в круге  с выколотым центром заданная функция представляется рядом
с выколотым центром заданная функция представляется рядом
 .
.
Главная часть лорановского разложения содержит лишь одно слагаемое.
2.Разложение в области  . Здесь ряд (7) расходится, поэтому представим слагаемое
. Здесь ряд (7) расходится, поэтому представим слагаемое  в другом виде:
в другом виде:  .
.
Теперь можем рассматривать прогрессию со знаменателем  :
:
 . (8)
. (8)
Ряд справа сходится, так как  , то есть
, то есть  .
.
Следовательно, заданная функция в области  представляется разложением только по отрицательным степеням
представляется разложением только по отрицательным степеням  :
:
 . ☻
. ☻
Задача 1. Разложить в ряд Лорана функцию  при
при  в кольце
в кольце  . Ответ:
. Ответ:  .
.
Пример 3. Функцию  в области
в области  разложить в ряд Лорана по степеням
разложить в ряд Лорана по степеням  .
.
Решение. Обозначим  и воспользуемся разложением (8):
и воспользуемся разложением (8):

Почленно дифференцируем равномерно сходящийся в области  ряд:
ряд:

Значит,  . ☻
. ☻
Пример 4. Функцию  разложить в ряд Лорана,
разложить в ряд Лорана,  .
.
Решение. Заменяя в известном разложении для синуса  на
на  , получим
, получим 
Значит, 
Правильная часть полученного разложения содержит лишь два слагаемых:  . В главной части
. В главной части  – бесконечное число слагаемых. ☻
– бесконечное число слагаемых. ☻
Задача 2. Разложить в ряд Лорана функцию  в окрестности точки
в окрестности точки  .
.
Указание. Воспользоваться формулой  и известным разложением для косинуса. Ответ:
и известным разложением для косинуса. Ответ:  .
.
Задача 3. В окрестности точки  (т.е. по степеням
(т.е. по степеням  ) разложить в ряд Лорана функцию
) разложить в ряд Лорана функцию  . Ответ:
. Ответ:  .
.