Теорема Остроградского-Гаусса
Экспериментально установленные закон Кулона и принцип суперпозиции позволяют полностью описать электростатическое поле заданной системы зарядов. Однако, свойства электростатического поля можно выразить в другой, более общей форме, не прибегая к представлению о кулоновском поле точечного заряда.
Введем новую физическую величину, характеризующую электрическое поле – поток  вектора напряженности
вектора напряженности  электрического поля. Понятие потока вектора
электрического поля. Понятие потока вектора  аналогично понятию потока вектора скорости при течении несжимаемой жидкости. Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка
аналогично понятию потока вектора скорости при течении несжимаемой жидкости. Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка  , в пределах которой напряженность
, в пределах которой напряженность 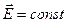 , т. е. электростатическое поле однородно. Произведение модуля вектора
, т. е. электростатическое поле однородно. Произведение модуля вектора  на площадь
на площадь  и на косинус угла
и на косинус угла  между вектором
между вектором  и нормалью
и нормалью 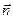 к площадке называется элементарным потоком вектора напряженности
к площадке называется элементарным потоком вектора напряженности  через площадку
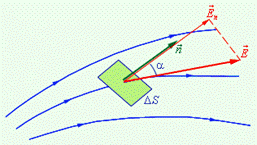
через площадку  (рис. 10.7):
(рис. 10.7):
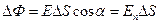 , (10.8)
, (10.8)
где 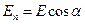 - проекция поля
- проекция поля  нанаправление нормали
нанаправление нормали 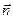 .
.
Рассмотрим теперь некоторую произвольную замкнутую поверхность 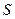 . В случае замкнутой поверхности всегда выбирается внешняя нормаль к поверхности, т. е. нормаль, направленная наружу области.
. В случае замкнутой поверхности всегда выбирается внешняя нормаль к поверхности, т. е. нормаль, направленная наружу области.
Если разбить эту поверхность на малые площадки, определить элементарные потоки поля через эти площадки, а затем их просуммировать, то в результате мы получим поток  вектора напряженности
вектора напряженности  через замкнутую поверхность
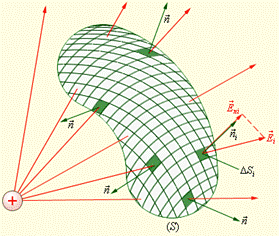
через замкнутую поверхность 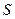 (рис. 10.8):
(рис. 10.8):
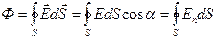 . (10.9)
. (10.9)
|
| Рис. 10.7 |
|
| Рис. 10.8 |
ТеоремаОстроградского-Гаусса утверждает: поток вектора напряженности электростатического поля  через произвольную замкнутую поверхность
через произвольную замкнутую поверхность 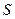 прямо пропорционален алгебраической сумме свободных зарядов, расположенных внутри этой поверхности:
прямо пропорционален алгебраической сумме свободных зарядов, расположенных внутри этой поверхности:
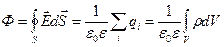 , (10.10)
, (10.10)
где 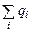 - алгебраическая сумма свободных зарядов, находящихся внутри поверхности
- алгебраическая сумма свободных зарядов, находящихся внутри поверхности 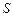 ,
, 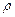 - объемная плотность свободных зарядов, занимающих объем
- объемная плотность свободных зарядов, занимающих объем  .
.
Если ввести вектор электрического смещения
 , (10.11)
, (10.11)
то теорему Остроградского-Гаусса можно выразить через поток  вектора
вектора 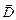 через замкнутую поверхность
через замкнутую поверхность 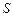 :
:
 . (10.12)
. (10.12)
Из теоремы Остроградского-Гаусса (10.10), (10.12) следует, что поток  не зависит от формы замкнутой поверхности
не зависит от формы замкнутой поверхности 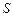 (сфера, цилиндр, куб и т.п.), а определяется только суммарным зарядом внутри этой поверхности.
(сфера, цилиндр, куб и т.п.), а определяется только суммарным зарядом внутри этой поверхности.
Используя теорему Остроградского-Гаусса, можно в ряде случаев легко вычислить напряженность электрического поля заряженного тела, если заданное распределение зарядов обладает какой-либо симметрией.
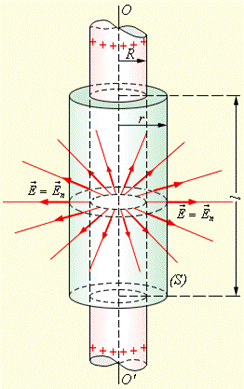
Рассмотрим задачу о вычисленииполя тонкостенного пологооднородно заряженного длинного цилиндра радиуса  (тонкой бесконечной заряженной нити). Эта задача имеет осевую симметрию. Из соображений симметрии электрическое поле должно быть направлено по радиусу. Выберем замкнутую поверхность
(тонкой бесконечной заряженной нити). Эта задача имеет осевую симметрию. Из соображений симметрии электрическое поле должно быть направлено по радиусу. Выберем замкнутую поверхность 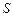 в виде цилиндра произвольного радиуса
в виде цилиндра произвольного радиуса 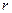 и длины
и длины 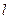 , закрытого с обоих торцов (рис. 10.9).
, закрытого с обоих торцов (рис. 10.9).
Для 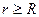 поток вектора напряженности
поток вектора напряженности  будет проходить через боковую поверхность цилиндра, площадь которой равна
будет проходить через боковую поверхность цилиндра, площадь которой равна 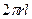 , так как поток через оба основания равен нулю. Используя теорему Остроградского-Гаусса в форме (10.10), получим:
, так как поток через оба основания равен нулю. Используя теорему Остроградского-Гаусса в форме (10.10), получим:
 , (10.13)
, (10.13)
где  - заряд на единицу длины цилиндра (линейная плотность заряда).
- заряд на единицу длины цилиндра (линейная плотность заряда).
Отсюда напряженность поля
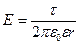 . (10.14)
. (10.14)
Этот результат не зависит от радиуса R заряженного цилиндра, поэтому он применим и к полю тонкой бесконечной однородно заряженной нити.
|
| Рис. 10.9 |
Для расчета напряженности поля внутри заряженного цилиндра выберем замкнутый цилиндр с 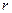 <
<  . Поскольку внутри этого цилиндра заряд отсутствует, то в соответствии с (10.13), поток
. Поскольку внутри этого цилиндра заряд отсутствует, то в соответствии с (10.13), поток  и поле
и поле  равны нулю.
равны нулю.
Аналогичным образом можно применять теорему Остроградского-Гаусса для расчета электрического поля и в других задачах, когда распределение зарядов обладает какой-либо симметрией, например, относительно центра, плоскости или оси. В каждом из таких случаев выбирают форму замкнутой гауссовой поверхности, исходя из симметрии задачи. Например, в случае центральной симметрии гауссову поверхность удобно выбирать в виде сферы с центром в точке симметрии. При осевой симметрии замкнутую поверхность выбирают в виде цилиндра, замкнутого с обоих торцов (как в рассмотренном выше примере).
Рассмотрим еще один примерсимметричного распределения зарядов– расчет поля равномерно заряженной плоскости с поверхностной плотностью заряда 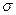 (заряд, приходящийся на единицу площади) (рис. 10.10).
(заряд, приходящийся на единицу площади) (рис. 10.10).

|
| Рис. 10.10 |
В этом случае гауссову поверхность S целесообразно выбрать в виде цилиндра некоторой длины, закрытого с обоих торцов. Ось цилиндра направлена перпендикулярно заряженной плоскости, а его торцы расположены на одинаковом расстоянии от нее. В силу симметрии поле равномерно заряженной плоскости везде направлено по нормали к плоскости. Применение теоремы Гаусса дает:
 ,
, 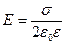 . (10.15)
. (10.15)
Используя теорему Остроградского-Гаусса и принцип суперпозиции, можно рассчитать напряженность поля, создаваемого двумя бесконечными параллельными разноименно заряженными плоскостями (поле внутри плоского конденсатора)
 , (10.16)
, (10.16)
и напряженность поля равномерно заряженной сферы радиуса 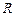 на расстоянии
на расстоянии 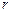 ≥
≥ 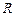 :
:
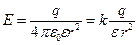 (10.17)
(10.17)