Вычисление определителей 2-го и 3-го порядка
Определитель 2-го порядка вычисляется по определению:
 .
.
Пример 1
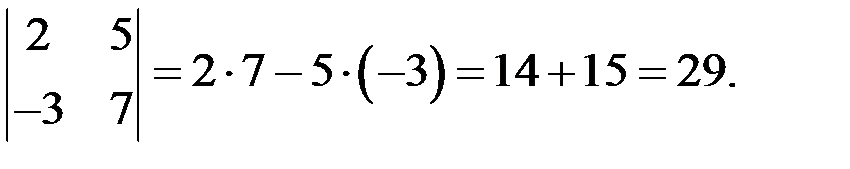
Для вычисления определителя 3-го порядка можно воспользоваться следующими правилами:
Правило Саррюса: дописать справа к элементам определителя сначала 1-й столбец, затем 2-й (можно внизу дописать первую и вторую строки), (рис.1), произведение элементов, стоящих на главной диагонали определителя, а также произведения элементов, стоящих на двух параллелях к ней, содержащих по 3 элемента – нужно взять со знаком «плюс», а произведение элементов побочной диагонали и двух параллелях к ней, содержащих по 3 элемента – нужно взять со знаком «минус» (рис. 1). Сумма этих шести произведений дает определитель 3-го порядка, соответствующий матрице А.
 ,
,
- - - + + +
Рис. 1
Пример 2
Вычислить  .
.
Решение
 ,
,
– – – + + +
таким образом:
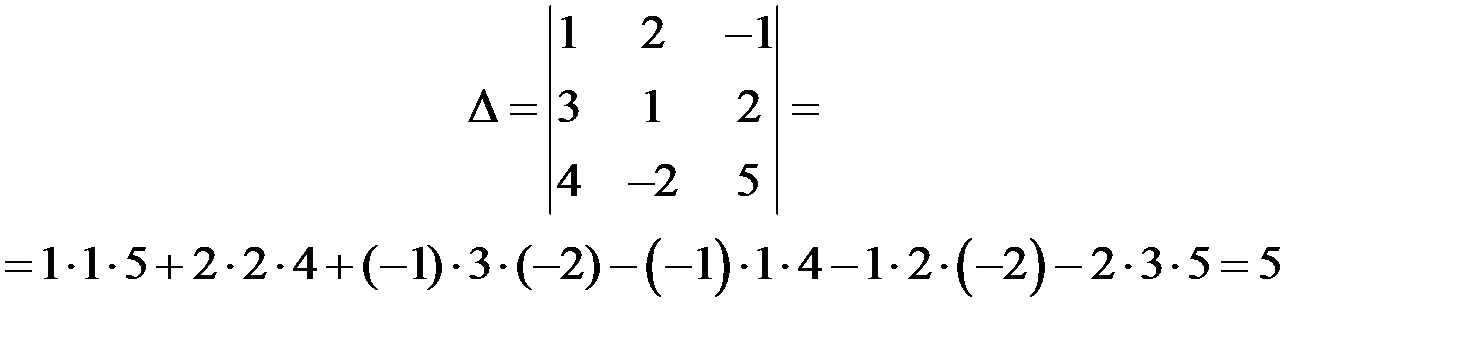
Правило треугольника:одно из трех слагаемых, со знаком «плюс» есть произведение элементов главной диагонали определителя, каждое из двух других – произведение элементов, лежащих на параллели к этой диагонали, и элемента из противоположного угла определителя, слагаемые со знаком «минус» строятся так же, но относительно побочной диагонали (рис.2).
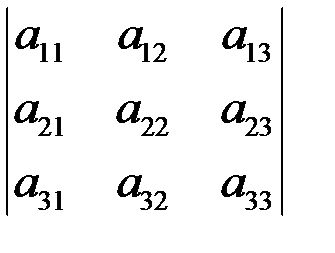
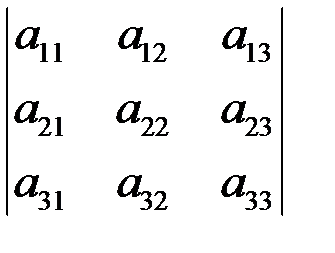
(+) (-)
Рис. 2