Проверка

Из уравнения (3) и расчетной схемы рис. I, б

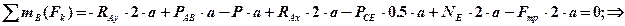
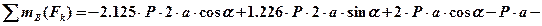
Если решение верное, то после подстановки числовых значений всех величин, как известных по условию задачи, так и определенных при ее решении, получаем:

 

Рис. I.

 

Варианты заданий

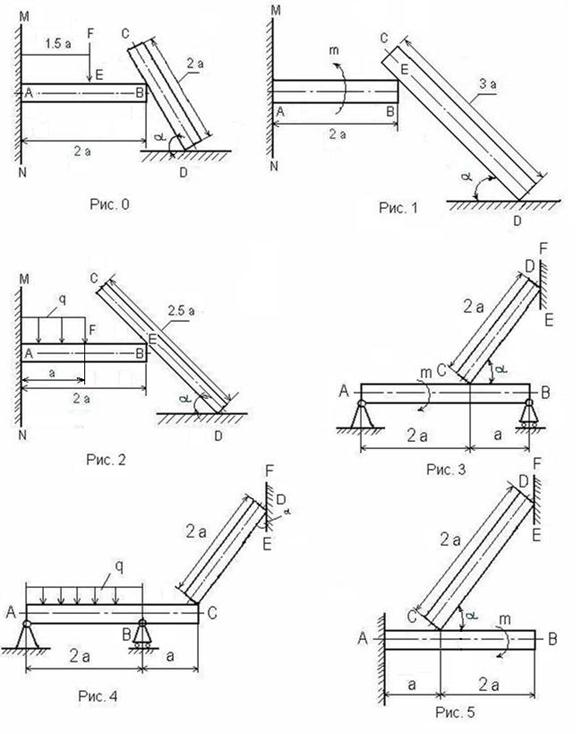
Задание 0. Однородный стержень CD длиной 2 a концом D опирается на шеро­ховатую поверхность, а серединой на стержень AB (рис. 0). Стержень AB жестко заделан концом A в стену MN. Угол наклона стержня CD - a = 60⁰. Трение в точке B отсутствует. Вес стержня длиной a (м) равен P (H). В точке E на стержень AB действует вертикальная сила F. Определить коэффициент трения f между стержнем CD и горизонтальной поверхностью (в точке D), а также реакции связи в точке A для следующих исходных данных (табл. 0).

Таблица 0

N варианта
a (м)	1.6	1.0	0.5	0.2	0.4	0.8	0.6	1.2	2.0	1.5
P (H)
F (H)

Задание 1. Однородный стержень CD длиной 3 а концом D опирается на шеро­ховатую поверхность, а точкой Е (DE = 2 a) на стержень АВ (рис. 1). Стержень АВ длиной 2 а жестко заделан в стену MN концом А. Угол наклона стержня CD -α= 45⁰. Трение в точке Е отсутствует. В середине стержня AB действует пара сил с момен­том m. Вес стержня длиной а (м) равен P (H). Определить коэффициент трения f между стержнем CD и горизонтальной поверхностью (в точке D), а также реакции связи в точке А для следующих данных (табл. 1).

Таблица 1

N варианта
a (м)	2.0	1.5	1.8	1.3	1.6	1.4	1.0	0.9	1.7	1.9
P (H)
m (Hм)

Задание 2. Однородный стержень CD длиной 2.5 а концом D опирается на шероховатую поверхность, а точкой Е (DE = 1.5 а) на стержень АВ (рис. 2). Стер­жень АВ длиной 2 а жестко заделан в стену MN концом А. Угол наклона стержня CD - α = 45⁰. Трение в точке Е отсутствует. На стержень АВ на участке AF = a действует равномерно распределенная нагрузка интенсивности q. Вес стержня дли­ной а (м) равен P (H). Определить коэффициент трения f между стержнем CD и горизонтальной поверхностью (в точке D), а также реакции связи в точке А для следующих данных (табл. 2).

Таблица 2

N варианта
a (м)	1.5	2.0	1.0	1.2	1.8	1.6	1.4	2.5	2.2	2.0
P (H)
q (H/м)

Задание 3. Два однородных стержня АВ и СD расположены как показано на рис. 3. Поверхность стены (EF) гладкая, а стержня АВ – шероховатая. Вес стержня длиной а (м) равен Р (H). Угол α=60⁰. На стержень АВ действует пара сил с момен­том m. Определить коэффициент трения f в точке С и реакции связей в точках А, В и D для следующих данных (табл. 3).

Таблица 3

N варианта
a (м)	1.0	1.1	1.2	0.8	0.6	1.4	1.5	0.7	1.0	1.3
P (H)
m (Hм)

Задание 4. Два однородных стержня АС и CD расположены, как показано на рис. 4. Поверхность стержня АС шероховатая, а стены (EF) – гладкая. На участок АВ стержня АС действует равномерно распределенная по длине нагрузка q = 7Н. Вес стержня длиной а (м) равен Р (Н). Определить коэффициент трения f в точке С и реакции связей в точках А, В и D для следующих данных (табл. 4).

Таблица 4

N варианта
a (м)	2.0	1.5	1.2	1.8	1.4	1.6	2.2	0.8	1.0	2.0
P (H)
α (град)

Задание 5. Два однородных стержня АВ и СD расположены как показано на рис. 5. Поверхность стены (EF) гладкая, а стержня АВ – шероховатая. На стержень АВ действует пара сил с моментом m. Вес стержня длиной а (м) равен Р (H). Угол α=60⁰. Определить коэффициент трения f в точке С и реакции связей в точках А и D для следующих данных (табл. 5).

 

Таблица 5

N варианта
a (м)	2.0	1.8	1.0	1.4	1.2	1.5	1.6	0.8	0.6	1.0
P (H)
m (Hм)

Задание 6. Два однородных стержня АВ и CD расположены, как показано на рис. 6. Поверхность стержня АВ шероховатая, а стены (EF) – гладкая. На стержень АВ в точке В действует сила F. Вес стержня длиной а (м) равен Р (Н). Угол α=45⁰. Определить коэффициент трения f в точке С и реакции связей в точках А и D для следующих данных (табл. 6).

Таблица 6

N варианта
a (м)	1.4	2.0	1.8	1.6	1.5	1.2	1.0	1.4	2.0	1.0
P (H)
F (H)

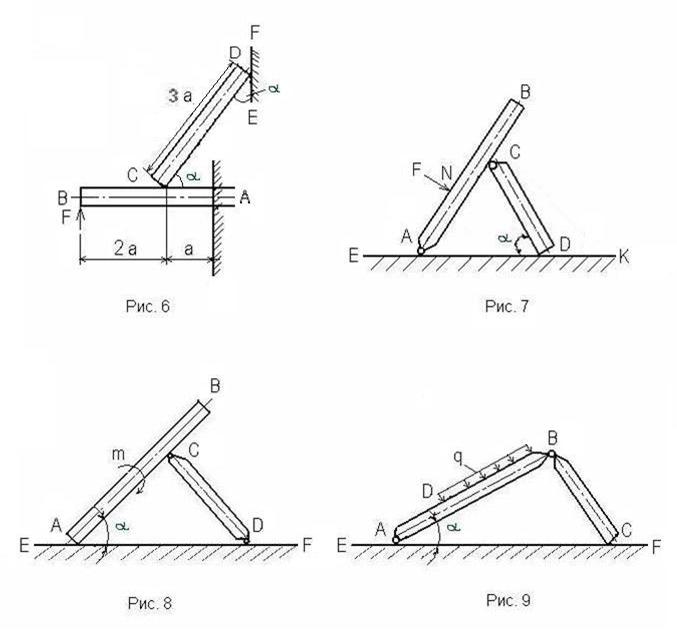
Задание 7. Однородный стержень AB длиной 3 a (рис. 7) закреплен в точке А и С шарнирно. В точке N к нему приложена сила F. AN = a; АС = CD = 2 a. Поверх­ность ЕК шероховатая. Вес стержня длиной а (м) равен P (H). Угол ADC – α = 60⁰. Определить коэффициент трения f между стержнем CD и поверхностью ЕК, а также величину реакции связи в точке А для следующих данных (табл. 7).

Таблица 7

N варианта
a (м)				1.5	2.5				1.5
P (H)
F (H)

Задание 8. Однородный стержень AB длиной 3 a (рис. 8) опирается концом А на шероховатую поверхность EF, а в точке С соединен со стержнем CD (AC = CD = 2 a). Вес стержня длиной а (м) равен P (H). Угол α = 45⁰. На стержень АВ действует пара сил с моментом m. Стержень CD в точке D закреплен шарнирно. Определить коэффициент трения f между стержнем АВ и поверхностью ЕF, а также реакции связи в точке D для следующих данных (табл. 8).

Таблица 8

N варианта
a (м)	0.8	0.6	0.9	1.0	1.5	1.2	1.3	0.7	1.1	1.0
P (H)
m (Hм)

Задание 9. Два однородных стержня АВ и ВС соединены шарнирно в точке В (рис. 9). Концом С стержень ВС опирается на шероховатую поверхность, а конец А стержня АВ закреплен шарнирно. На участок DB стержня АВ действует равномерно распределенная нагрузка интенсивности q. Длина DB = 2 a; AB = AC = 3 a; α = 30⁰. Вес стержня длиной а (м) равен Р (Н). Определить коэффициент трения в точке С между стержнем ВС и поверхностью EF, а также реакции связи в точках А и В для следующих данных (табл. 9).

Таблица 9

N варианта
a (м)	0.5	0.8	1.0	1.5	1.2	0.9	0.6	1.3	1.0	1.5
P (H)							0.8
q (H/м)

 

 

 

российский государственный геологоразведочный университет имени серго орджоникидзе (МГРИ-РГГРУ) кафедра механики И ИНЖЕНЕРНОЙ ГРАФИКИ Расчетная работа по теоретической механике   Равновесие системы тел под действием плоской произвольной системы сил с учетом сил трения (скольжения) Вариант N 5 (8)   Выполнил: студент группы     Проверил: профессор каф. механики     Москва, 2014 год