Решение

1. Для рассмотрения условий равновесия данной системы тел необходимо составить расчетную схему, используя аксиому связей. Решая задачу в соответствии с этой аксиомой, мысленно отбрасываем связи и заменяем их действие силами реакций отброшенных связей. Другими словами, несвободную систему тел превращаем в свободную. (рис. I, б).

2. Исследуя составленную расчетную схему, получаем, что заданная система тел находится в равновесии под действием трех внешних активных силовых факторов (известных) и четырех реактивных сил (неизвестных). Рассматриваемая система семи силовых факторов является плоской произвольной системой сил. Условия равновесия такой системы определяются тремя уравнениями (I).

(1)

(2)

(3)

Таким образом, для данной расчетной схемы число неизвестных величин пре­вышает число возможных уравнений равновесия.

Для получения дополнительных уравнений равновесия, и имея в виду, что каж­дое тело системы находится в равновесии, рассмотрим условия равновесия каждого тела или одного из них в отдельности.

3. На стержень АВ, если рассматривать его как отдельное свободное тело, дей­ствуют шесть силовых факторов: два внешних, активных (известных), и четыре реакции связи в шарнирах А и B. Эта расчетная схема изображена на рис. I, в.

Для стержня АВ, как свободного тела, условия равновесия определяются также тремя уравнениями:

(1')

(2')

(3')

4. Рассматривая совместно две расчетные схемы, имеем систему из шести урав­нений, определяющих условия равновесия как всей системы тел, так и отдельно стержня АВ. В эти уравнения входят шесть неизвестных, которые необходимо определить.

Из уравнения (3) и расчетной схемы рис. I, б

Из уравнения (2) для расчетной схемы рис. I, б

Из уравнения (3') для расчетной схемы рис. I, в

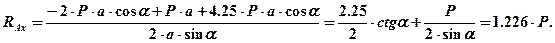
Из уравнений (1) и (1')

Из уравнения (II)