Контрольная работа № 3. Задания.
1. Найти неопределенные и определенный интегралы. В двух первых примерах (п. а) и б) проверить результаты дифференцированием.
| № | а | б | в | г |
| 1.1 | 
| 
| 
| 
|
| 1.2 | 
| 
| 
| 
|
| 1.3 | 
| 
| 
| 
|
| 1.4 | 
| 
| 
| 
|
| 1.5 | 
| 
| 
| 
|
| 1.6 | 
| 
| 
| 
|
| 1.7 | 
| 
| 
|
|
| 1.8 | 
| 
| 
| 
|
| 1.9 | 
| 
| 
| 
|
| 1.10 | 
| 
| 
| 
|
| 1.11 | 
| 
| 
| 
|
| 1.12 | 
| 
| 
| 
|
| 1.13 | 
|
| 
| 
|
| 1.14 | 
| 
| 
| 
|
| 1.15 | 
| 
| 
| 
|
| 1.16 | 
| 
| 
| 
|
| 1.17 | 
| 
| 
| 
|
| 1.18 | 
| 
| 
| 
|
| 1.19 | 
| 
| 
| 
|
| 1.20 | 
|
| 
| 
|
2. Геометрические приложения определенного интеграла
2.1. Вычислить площадь фигуры, ограниченной параболой 
и прямой 
2.2. Вычислить площадь фигуры, ограниченной параболой 
и прямой 
2.3. Вычислить площадь фигуры, ограниченной параболой 
и прямой 
2.4. Вычислить площадь фигуры, ограниченной параболой 
и прямой 
.
2.5. Вычислить площадь фигуры, ограниченной графиком функции 
, 
и прямой 
.
2.6. Вычислить площадь фигуры, ограниченной графиком функции , и прямой 
.
2.7. Вычислить площадь фигуры, ограниченной графиком функции 
, 
и прямой .
2.8. Вычислить площадь фигуры, ограниченной графиком функции , и прямой .
2.9. Вычислить площадь фигуры, ограниченной графиком функции 
, осью ОХ и прямыми 
.
2.10. Вычислить площадь фигуры, ограниченной линиями 
2.11. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной параболами 
и 
2.12. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной полуэллипсом 
.
2.13. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной гиперболой 
и прямыми 
.
2.14. Вычислить объем тела, полученного вращением вокруг оси О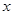 
фигуры, ограниченной параболой 
и кубической параболой 
2.15. Вычислить объем тела, полученного вращением вокруг оси О 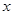фигуры, ограниченной параболами 
и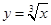 
.
2.16. Вычислить объем тела, полученного вращением вокруг оси О 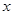фигуры, ограниченной параболами 
и .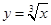
2.17. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной параболами и 
2.18. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной полуэллипсом 
.
2.19. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной гиперболой 
и прямыми 
.
2.20. Вычислить объем тела, полученного вращением вокруг оси О фигуры, ограниченной параболой 
и кубической параболой 