Б. Если дано уравнение вида
Ғ(у(п), х)=0(11.5'),
to разрешив его относительно у(п) мы приведем его к виду (11.5). Но иногда удается разрешить это уравнение в элементарных функциях лишь относительно х или, в более общем случае, выразить х и у в функции параметра t, тогда интеграция уравнения (11.5;) может быть сведена к квадратурам, выраженным явно. Пусть параметрические уравнения, эквивалентные уравнению (11.5), суть
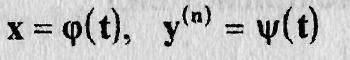(11.5")
По определению dy(n-1) = y(n)dx или в нашем случае
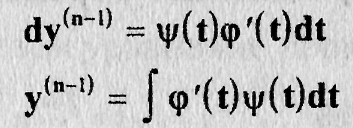откуда
Далее
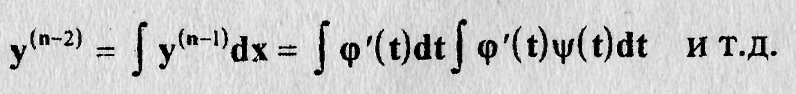
В результате получаем
x =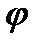 
(t) y = o(t,C,,...,Cn) (11.10)
Пример 11.4.:еуn+уn = х. Здесь разрешение относительно уn в элементарных функциях невозможно; за параметр tестественно взять
Уn, и мы получаем параметрические уравнения x-e' + t, yn=t. Отсюда
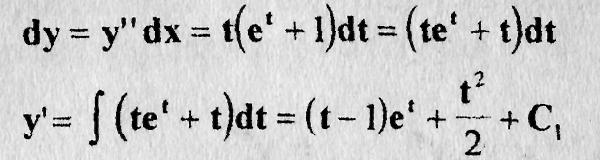
Далее
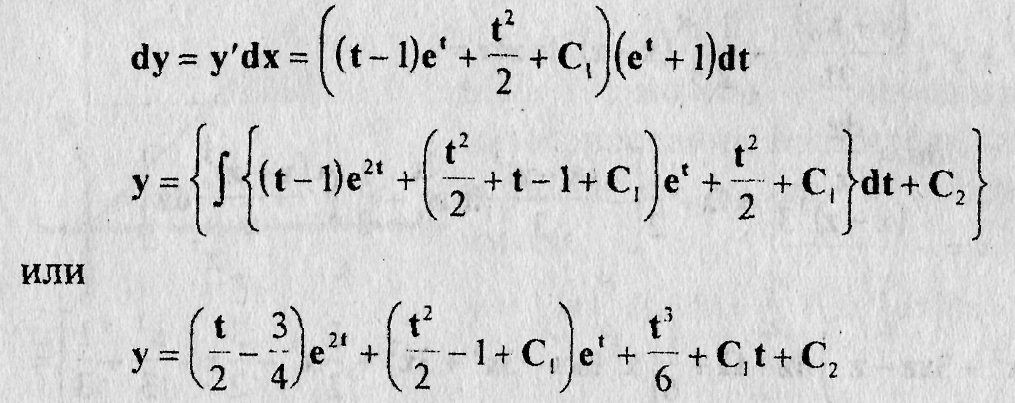
Последняя формула вместе с выражением для х, х = е' +t дает параметрическое представление общего решения данного уравнения.