Дифференциальное уравнение первого порядка.

Если в уравнении ( ) входит только первая производная от искомой функции, то это дифференциальное уравнение первого порядка. Самое общее дифференциальное уравнение первого порядка имеет вид

(7.16)

Где -заданная непрерывная функция трех своих аргументов: в частности, она может не зависит от х или от у, но непременно должна содержать .

Если уравнение (7.6) определяет как неявную функцию двух остальных аргументов, то его можно представить в виде разрешенном относительно

= (7.17)

Здесь -непрерывная заданная функция от х и у.

В дифференциальном уравнении (7.16) или (7.17) х является независимым переменным, у –искомой функцией.

 

Определение7.4дифференциальное уравнение первого порядка есть соотношение, связывающее искомую функцию, независимые переменные и первую производную от искомой функции.

 

Определение 7.5 Решением дифференциального уравнения первого порядка называется всякая функция 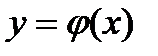, которая будучи подставлена в уравнение (7.16) или (7.17) обратит его в тождество.

Для дифференциального уравнения (7.17) справедлива следующая теорема, так называемая теорема существования.

 

Теорема 7.1если в уравнении (7.17) функция непрерывна и ее частная производная непрерывна в некоторой область содержащей некоторую точку , то существует единственное решение этого уравнения

,

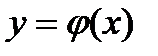Удовлетворяющее условию

при

Геометрический смысл теоремы заклюается в том, что существует и при том единственная функия 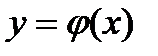, график которой проходит через точку .

 

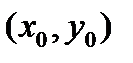Пример 7.7 :Рассмотрим задачу

при (7.18)

Где 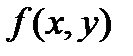является непрерывной функцией и областью определения этой функии является множество всех .

Легко видно, что 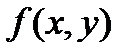и , т.е выполняется условие теоремы. Решение этого уравнения является функция

Определим С из условия что при , т.е , откуда С=1/2.

Таким образом, = .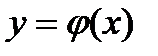

 

 

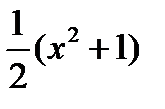Условие , что при х=х₀ функция у должна равняться начальному заданному числу у₀, называется начальным условием. Она часто записывается в виде

или

 

Определение 7.6Общим решением дифференциального уравнения первого порядка называется функция 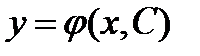, которая зависит от одного произвольного постоянного С и удовлетворяет следующим условиям:

А) она удовлетворяет дифференциальному уравнению при любом конкретном значении С постоянного С.

Б) какова бы ни было начальное условие 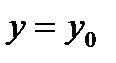при то есть можно найти такое значение С=С₀ что функция удовлетворяет данному начальному условию.

Эти все условия будут удовлетворены, тогда и только тогда, когда выполняется условие теоремы существования и единственности.

В процессе разыскания общего решения дифференциального уравнения мы нередко приходим к соотношению вида

 

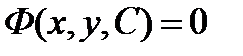(7.19)

Не разрешено относительно у. разрешив это соотношение относительно у, получим общее решение.

Однако, выразить у через соотношение (7.19) в элементарных функциях не всегда оказывается возможным. В таком случае общее решение дифференциального уравнения остается в неявном виде.

Равенства вида:

, неявно задающее общее решение, называется общим интегралом дифференциального уравнения.

 

Определение 7.7:Частным решением называется любая функция 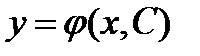, если в последнем произвольном постоянном С придать определенное значение С=С_0.

соотношение 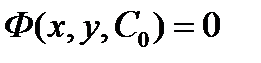называется частным интегралом уравнения.

 

Пример 7.8: