Подобие лопастных нагнетателей. Пересчет характеристик

Сложность аэрогидродинамических процессов, происходящих в лопастных нагнетателях, делает невозможным теоретический расчет их характеристик. Поэтому они определяются на основе экспериментальных исследований. В то же время при разработке новых конструкций необходимо, на основе испытаний модельного образца предсказать рабочие параметры предназначенных к серийному выпуску машин. И здесь используется теория гидродинамического подобия, в соответствии с которой нагнетатели гидродинамически подобны, если соблюдены следующие три условия подобия.

Геометрическое подобие, означающее пропорциональность соответствующих размеров нагнетателя (диаметров входа и выхода из колеса D1 и D2, ширины колеса b и т.д.), т.е.

. (3.3)

Кинематическое подобие, предусматривающее пропорциональность скоростей u в сходственных точках потока, т.е.

.(3.4)

Равенство углов установки лопаток на входе и выходе из колеса и КПД, т.е.

; ; . (3.5)

Здесь индексом «м» обозначены параметры модельного нагнетателя, «н» – натуральной машины.

Для сопоставления разных конструкций нагнетателей в качестве критерия подобия используется так называемый коэффициент быстроходности ns.

Коэффициентом быстроходности насоса называют такую частоту вращения, при которой он при напоре H=1м вод.ст. имеет подачу L=0,075 м3/с при максимальном КПД:

ns = 3,65 . (3.6)

Коэффициент быстроходности вентилятора вычисляется по формуле:

ns=5,5 , (3.7)

где L определяется в м3/с; P - в Па при максимальном КПД.

Нагнетатели, имеющие одинаковые коэффициенты быстроходности, являются подобными.

Рассмотрим теперь применение принципов аэрогидродинамического подобия для практических расчетов.

Как уже отмечалось выше, испытания нагнетателей с целью получения их характеристик, производится при условии сохранения постоянства трех величин: 1) формы и размера элементов машины; 2) режима ее работы (n = const); 3) неизменного состояния перемещаемой среды (ρ =const).

Таким образом, возникает необходимость получения характеристик нагнетателя для случая, когда одна или две, или все три выше указанные величины отличаются от их значений в режиме испытаний. Как же влияет изменение этих величин на характеристики нагнетателей?

Влияние изменения частоты вращения. Пусть известная характеристика соответствует частоте вращения n0. Измененная частота вращения n. Отношение окружных скоростей

 

.

Так как геометрическое подобие параллелограмма скоростей не нарушается, то скорости в любых точках изменяются пропорционально n. Производительность L=υF. Площадь F= const. Следовательно,

. (3.8)

 

Из формулы Эйлера следует

.

Отсюда получим

. (3.9)

Так как мощность изменяется пропорционально произведению PL, то

. (3.10)

Пример 3.1.Характеристика задана точками

 

P, Па
L, м3/ч
N, кВт 1,1 1,25 1,35 1,7 1,8

 

Рассчитать характеристики вентилятора при увеличении частоты вращения в 1,2 раза. Пересчет производится по формулам:

; ; .

 

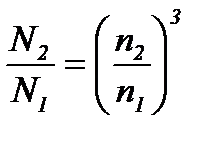После перерасчета характеристика примет вид

P, Па
L, м3/ч
N, кВт 1,9 2,16 2,33 2,94 3,11

 

Влияние изменения геометрических размеров. В конкретных конструкциях нагнетателей пропорции между геометрическими размерами сохраняются неизменными. В качестве характерной величины принимается диаметр колеса D2. Итак, пусть известны характеристики для диаметра D2 = D0. Требуется найти значения характеристик для D2 = D.

.

Площадь F ∼ D2. Отношение производительности равно

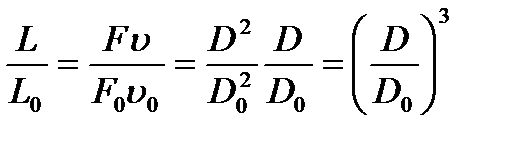. (3.11)

 

Давление изменяется по зависимости

. (3.12)

Отношение мощностей равно

. (3.13)

Влияние изменения плотности перемещаемой среды. Пусть известны характеристики при плотности ρ0. Требуется найти характеристики при плотности ρ. Так как частота вращения и геометрические размеры не изменяются, то из зависимости L=υF следует, что объемная производительность не зависит от плотности (температуры) перемещаемой среды, т.е.

. (3.14)

Давление прямо пропорционально плотности перемещаемой среды:

. (3.15)

Аналогично изменяется и мощность:

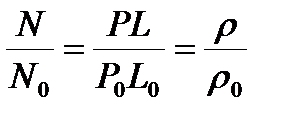. (3.16)

Так как плотность зависит от температуры перемещаемой среды, то из формулы (3.16) следует важный практический вывод. Если в условиях эксплуатации может изменяться плотность перемещаемой среды, то мощность электродвигателя следует рассчитывать на максимально возможную в эксплуатации плотность перемещаемой среды (минимальную температуру).