Полный дифференциал.
Полное приращение 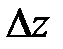 функции z определяется равенством
функции z определяется равенством
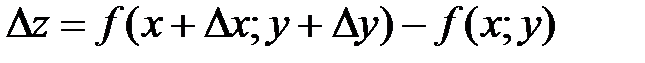 . (1)
. (1)
Замечание. Полное приращение функции, вообще говоря, не равно сумме частных приращений: 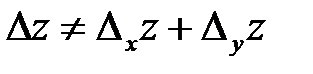 .
.
Определение 2. Функция  называется дифференцируемой в точке
называется дифференцируемой в точке  , если ее полное приращение в этой точке можно представить в виде
, если ее полное приращение в этой точке можно представить в виде
 , (2)
, (2)
где 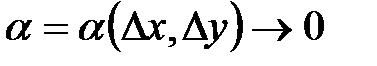 и
и 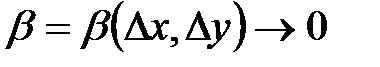 при
при  ,
,  .
.
Сумма первых двух слагаемых в равенстве (2) представляет собой главную часть приращения функции.
Определение 3. Полным дифференциалом (или просто дифференциалом)функции  называется главная часть приращения функции, линейная относительно
называется главная часть приращения функции, линейная относительно  и
и 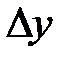 . Обозначается символом
. Обозначается символом  :
:
 . (3)
. (3)
Для независимых переменных x и y полагают  и
и  . Поэтому равенство (3) можно представить в виде
. Поэтому равенство (3) можно представить в виде
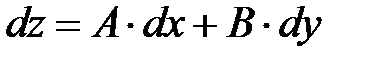 . (4)
. (4)
Теорема 1. (необходимое условие дифференцируемости функции). Если функция  дифференцируема в точке
дифференцируема в точке 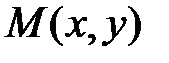 , то она непрерывна в этой точке, имеет в ней частные производные
, то она непрерывна в этой точке, имеет в ней частные производные  и
и  , причем
, причем  ,
,  .
.
Как следствие теоремы получаем формулу для вычисления полного дифференциала. Формула (4) принимает вид:
 . (5)
. (5)
Теорема 2 (достаточное условие дифференцируемости функции). Если функция  имеет непрерывные частные производные
имеет непрерывные частные производные  и
и  в точке
в точке 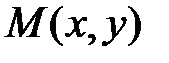 , то она дифференцируема в этой точке и ее полный дифференциал выражается формулой (5).
, то она дифференцируема в этой точке и ее полный дифференциал выражается формулой (5).
Рассмотрим типичные примеры, для решения которых используются приведенные определения, теоремы и понятия:
Пример 1. Найти частные производные функций:
а)  ; б)
; б)  ; в)
; в) 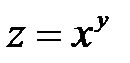 .
.
Решение.
а) Чтобы найти частную производную по x, считаем y постоянной величиной. Таким образом,  . Аналогично, дифференцируя по y, считаем x постоянной величиной, т.е.
. Аналогично, дифференцируя по y, считаем x постоянной величиной, т.е.  .
.
б) Чтобы найти частную производную по x, считаем y постоянной величиной. Таким образом, 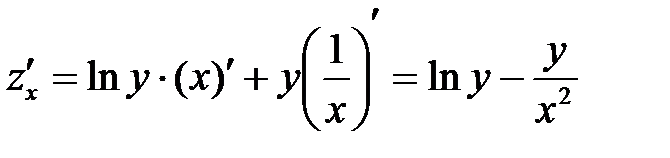 . Аналогично, дифференцируя по y, считаем x постоянной величиной, т.е.
. Аналогично, дифференцируя по y, считаем x постоянной величиной, т.е.  .
.
в)При фиксированном y имеем степенную функцию от x. Таким образом,  . При фиксированном x функция является показательной относительно y и
. При фиксированном x функция является показательной относительно y и  .
.
Пример 2. Показать, что функция  удовлетворяет уравнению
удовлетворяет уравнению
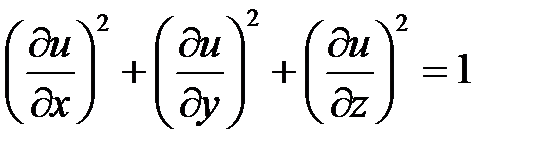 .
.
Решение.
Находим
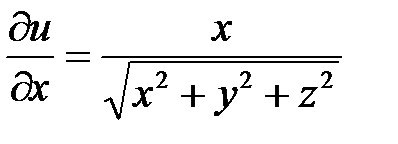 (при постоянных y и z);
(при постоянных y и z);
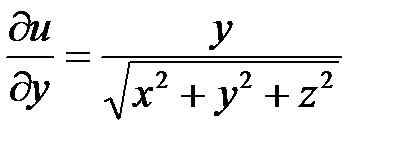 (при постоянных x и z);
(при постоянных x и z);
 (при постоянных x и y).
(при постоянных x и y).
Возводим эти выражения в квадрат и подставляем в левую часть заданного уравнения:
 .
.
Получаем тождественное равенство, т.е. функция u удовлетворяет уравнению.
Пример 3. Поток пассажиров z выражается функцией 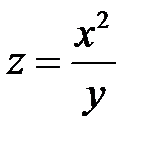 , где x – число жителей; y – расстояние между городами. Найти частные производные этой функции и пояснить их смысл.
, где x – число жителей; y – расстояние между городами. Найти частные производные этой функции и пояснить их смысл.
Решение.
Производная  показывает, что при одном и том же расстоянии между городами увеличение потока пассажиров пропорционально удвоенному числу жителей. Производная
показывает, что при одном и том же расстоянии между городами увеличение потока пассажиров пропорционально удвоенному числу жителей. Производная 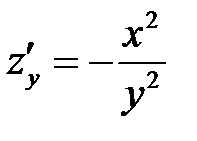 показывает, что при одной и той же численности жителей увеличение потока пассажиров обратно пропорционально квадрату расстояния между городами.
показывает, что при одной и той же численности жителей увеличение потока пассажиров обратно пропорционально квадрату расстояния между городами.
Пример 4. Пусть  – производственная функция, где x – затраты живого труда, y – затраты овеществленного труда. Найти эластичность функции:
– производственная функция, где x – затраты живого труда, y – затраты овеществленного труда. Найти эластичность функции:  и
и  в точке
в точке 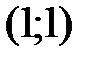 .
.
Решение.
Приближенный процентный прирост функции z, соответствующий приращению независимой переменой x на 1%,
 ,
,
а приближенный процентный прирост функции z, соответствующий приращению независимой переменой y на 1%,
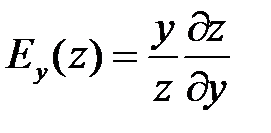 .
.
Найдем частные производные по x и по y:
 ,
, 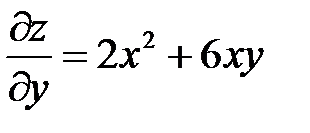 .
.
Тогда
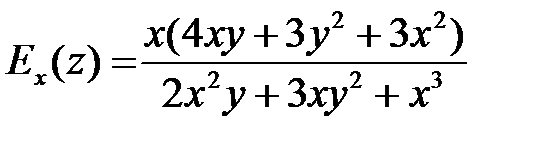 ,
, 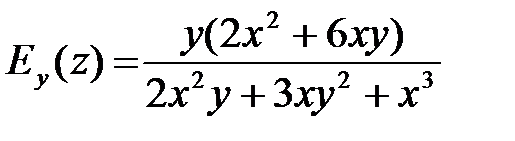 .
.
В заданной точке  ,
, 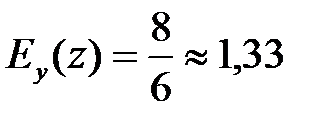 . С увеличением затрат живого труда на 1% объем производства увеличится на 0,67%, а с увеличением затрат овеществленного труда на 1% объем производства увеличится на 1,33%.
. С увеличением затрат живого труда на 1% объем производства увеличится на 0,67%, а с увеличением затрат овеществленного труда на 1% объем производства увеличится на 1,33%.
Пример 5. Найти дифференциал функции  .
.
Решение.
1. Находим частные производные
 ;
;  .
.
2. Используя формулу (5) получим выражение для дифференциала
 .
.