Частные производные первого порядка для функций двух переменных. Полный дифференциал

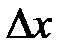1. Частные производные. Пусть задана функция . Так как x и y – независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной x приращение , сохраняя значение y неизменным. Тогда z получит приращение, которое называется частным приращением z по x и обозначается . Итак,

.

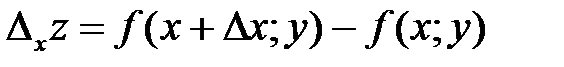Аналогично получаем частное приращение z по y:

.

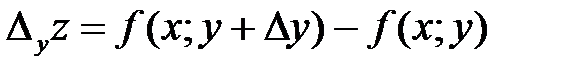Определение 1. Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при произвольном стремлении последнего к нулю (если этот предел существует).

Обозначается частная производная так: 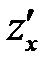, или , , или , .

Таким образом, для функции по определению

;

.

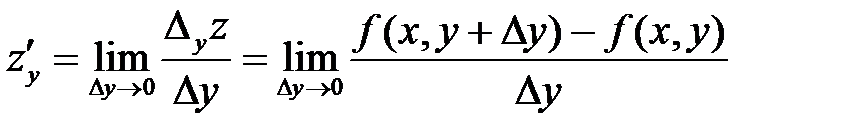Нахождение производной 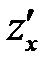называется дифференцированием функции z по аргументу x, а точка 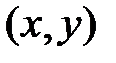называется точкой дифференцирования.

Из определения частных производных следует,чтодля нахождения производной 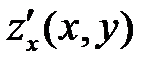надо считать постоянной переменную y, а для нахождения 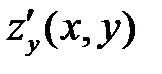– переменную x.

При этом правила вычисления их остаются теми же, что и для функции одной переменной, и только требуется помнить по какой переменной ищется производная.

Из определения следует геометрический смысл частной производной функции двух переменных: частная производная () – угловой коэффициент касательной к линии пересечения поверхности и плоскости ( ) в соответствующей точке.

Физический смысл частной производной: 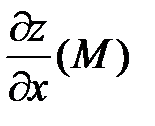– это скорость изменения функции в точке М в направлении оси 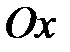, а 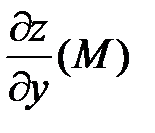– в направлении оси .