Основные понятия и определения для функций двух и нескольких переменных
Определение 1. Закон (правило) по которому каждой паре 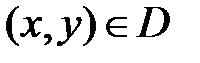 независимых переменных ставиться в соответствие определенное значение
независимых переменных ставиться в соответствие определенное значение 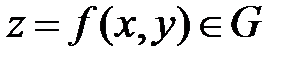 называется функцией двух переменных.
называется функцией двух переменных.
Например, площадь прямоугольника представляет собой функцию двух переменных.
Замечание. Если паре значений 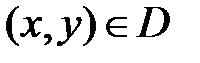 соответствует одно значение
соответствует одно значение 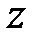 , то функция называется однозначной. В остальных случаях – многозначной.
, то функция называется однозначной. В остальных случаях – многозначной.
Определение 2. Пусть имеется n различных переменных величин, и каждому набору их значений ( 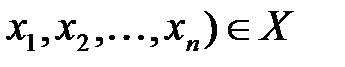 соответствует определенное значение переменной величины
соответствует определенное значение переменной величины  . Тогда говорят, что задана функция нескольких переменных
. Тогда говорят, что задана функция нескольких переменных 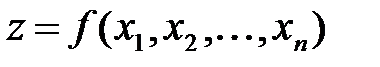 .
.
Например, объем параллелепипеда – функция трех переменных.
Переменные 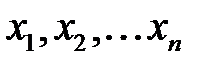 называются независимыми переменными, или аргументами, z – зависимой переменной, а символ f означает закон соответствия. Множество X называется областью определения функции. Очевидно, что X – подмножество n-мерного пространства.
называются независимыми переменными, или аргументами, z – зависимой переменной, а символ f означает закон соответствия. Множество X называется областью определения функции. Очевидно, что X – подмножество n-мерного пространства.
Обычно функция нескольких переменных задается аналитически (явно или неявно), таблично, графически (для случая функции двух переменных).
В дальнейшем, для простоты изложения, будем рассматривать функцию двух переменных, так как все важнейшие факты теории функции нескольких переменных наблюдаются уже на функциях двух переменных и обобщаются на случай большего числа переменных.
Как и в случае одного независимого переменного, функция двух переменных существует, вообще говоря, не при любых значениях x и y.
Определение 3.Совокупность пар 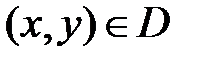 значений x и y, при которых функция
значений x и y, при которых функция 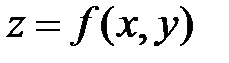 имеет смысл, называется областью определения функции.
имеет смысл, называется областью определения функции.
Область определения наглядно иллюстрируется геометрически. Если каждую пару значений x и y мы будем изображать точкой  в плоскости Oxy, то область определения функции
в плоскости Oxy, то область определения функции  изобразится в виде некоторой совокупности точек на плоскости, т.е. части плоскости, в частности, может быть и вся плоскость.
изобразится в виде некоторой совокупности точек на плоскости, т.е. части плоскости, в частности, может быть и вся плоскость.
Определение 4. Графиком функции двух переменных 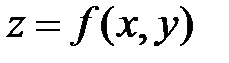 называется множество точек трехмерного пространства
называется множество точек трехмерного пространства  аппликата z которых связана с абсциссой x и ординатой y функциональным соотношением
аппликата z которых связана с абсциссой x и ординатой y функциональным соотношением 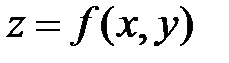 .
.
График функции двух переменных 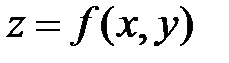 , вообще говоря, представляет собой некоторую поверхность в трехмерном пространстве.
, вообще говоря, представляет собой некоторую поверхность в трехмерном пространстве.
Как правило, построение поверхности оказывается довольно трудной задачей и поверхность обладает меньшей наглядностью, чем линия на плоскости. В связи с этим оказывается удобным геометрически описывать функцию двух переменных, не выходя в трехмерное пространство. Средством такого описания являются линии уровня.
Определение 5. Линией уровня  функции двух переменных
функции двух переменных 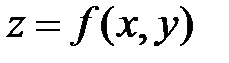 называется линия на плоскости
называется линия на плоскости 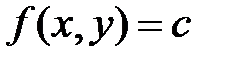 . В каждой точке, лежащей на этой линии, функция
. В каждой точке, лежащей на этой линии, функция 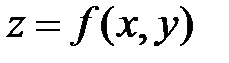 принимает значение, равное с.
принимает значение, равное с.
Число с в этом случае называется уровнем.
Обычно берут арифметическую прогрессию чисел 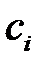 с постоянной разностью h; тогда по взаимному расположению линий уровня можно получить представление о форме поверхности, описываемой функцией
с постоянной разностью h; тогда по взаимному расположению линий уровня можно получить представление о форме поверхности, описываемой функцией 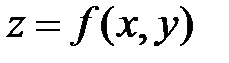 . Там, где функция изменяется быстрее, линии уровня сгущаются, а там, где поверхность пологая, линии уровня располагаются реже.
. Там, где функция изменяется быстрее, линии уровня сгущаются, а там, где поверхность пологая, линии уровня располагаются реже.
Многие примеры линий уровня хорошо известны. Например, параллели и меридианы на глобусе – это линии уровня функций широты и долготы. Синоптики публикуют карты с изображением изотерм – линий уровня температуры. Линиями уровня обозначают глубину морей и высоту гор на географических картах.
Определение 6. Поверхностью уровня (эквипотенциальной поверхностью) 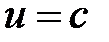 функции
функции  называется поверхность
называется поверхность 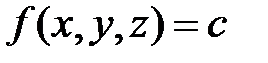 , в точках которой функция
, в точках которой функция  сохраняет значение, равное с.
сохраняет значение, равное с.
Придавая, постоянной с, различные числовые значения, получим семейство поверхностей уровня. Через каждую точку пространства проходит одна поверхность уровня.
Во всех точках поверхности уровня физическое явление протекает одинаково.
Рассмотрим типичные примеры, для решения которых используются приведенные определения и понятия:
Пример 1. Найти область определения функции  .
.
Решение. Для того, чтобы z имело действительное значение, нужно, чтобы под корнем стояло положительное число, т.е. x и y должны удовлетворять неравенству 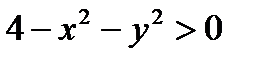 или
или  . Все точки
. Все точки 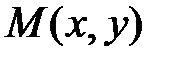 , координаты которых удовлетворяют указанному неравенству, лежат в круге радиуса 2 с центром в начале координат, исключая границу этого круга (рис.1).
, координаты которых удовлетворяют указанному неравенству, лежат в круге радиуса 2 с центром в начале координат, исключая границу этого круга (рис.1).
Пример 2. Найти область определения функции  .
.
| x |
| y |
| 2 |
| -2 |
| 2 |
| -2 |
| Рис.1. |
| x |
| y |
| 2 |
| -2 |
| 2 |
| -2 |
Решение. Так как арксинус определен для значений аргументов не превосходящих по модулю 1, то должно удовлетворяться неравенство
 , которое равносильно двойному неравенству
, которое равносильно двойному неравенству 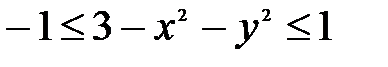 которое равносильно неравенствам:
которое равносильно неравенствам: 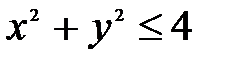 и
и 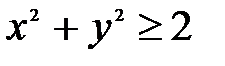 . Множество значений x и y, удовлетворяющих первому из указанных неравенств, представляет собой «внутренность» круга радиуса 2 с центром в точке
. Множество значений x и y, удовлетворяющих первому из указанных неравенств, представляет собой «внутренность» круга радиуса 2 с центром в точке  . Решения второго неравенства – «внешность» круга радиуса
. Решения второго неравенства – «внешность» круга радиуса 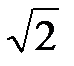 с центром в точке
с центром в точке  . В обоих случаях, так как неравенство не строгое, входит окружность круга. Таким образом, область определения представляет собой кольцо (рис.2).
. В обоих случаях, так как неравенство не строгое, входит окружность круга. Таким образом, область определения представляет собой кольцо (рис.2).
| Рис.2. |
Пример 3. Найти область определения функции
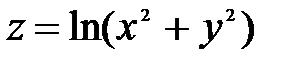 .
.
Решение. Так как логарифмы определены для положительных чисел, то должно удовлетворяться неравенство 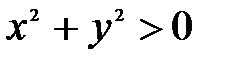 , которое справедливо для всех значений переменных x и y, кроме
, которое справедливо для всех значений переменных x и y, кроме 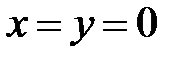 . Следовательно, областью определения данной функции является вся плоскость Oxy, кроме начала координат (рис.3).
. Следовательно, областью определения данной функции является вся плоскость Oxy, кроме начала координат (рис.3).
| x |
| y |
| 0 |
| Рис.3 |
Пример 4. Построить линии уровня функции  .
.
Решение. Пересечем данную поверхность плоскостью 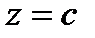
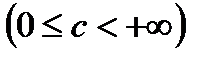 . Задавая с различные значения, например, с=0, 1, 2, …, получим семейство линий уровня, представляющих собой концентрические окружности (рис.4). При с = 0 окружность вырождается в точку (0, 0). Из того, что линиями уровня оказались окружности с центрами в начале координат, следует, что графиком данной функции должна быть поверхность вращения вокруг оси Oz. Действительно, как известно из аналитической геометрии, уравнение
. Задавая с различные значения, например, с=0, 1, 2, …, получим семейство линий уровня, представляющих собой концентрические окружности (рис.4). При с = 0 окружность вырождается в точку (0, 0). Из того, что линиями уровня оказались окружности с центрами в начале координат, следует, что графиком данной функции должна быть поверхность вращения вокруг оси Oz. Действительно, как известно из аналитической геометрии, уравнение  определяет параболоид вращения (рис.5).
определяет параболоид вращения (рис.5).
| x |
| 0 |
| y |
| z |
| Рис.5 |
| x |
| y |
| Рис.4 |
Пример 5. Построить поверхности уровня функции  .
.
Решение. Здесь поверхностями уровня будут поверхности, заданные уравнением 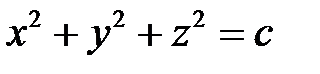 . Задавая с различные значения, например,
. Задавая с различные значения, например,
с=0, 1, 2, …, получим семейство поверхностей уровня, представляющих собой концентрические сферы с радиусом 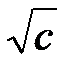 . При
. При  сфера вырождается в точку
сфера вырождается в точку  .
.