Гидростатическое давление и его свойства

ГИДРОСТАТИКА

Силы, действующие в жидкости.

Гидростатическое давление и его свойства

Для механической системы (выделенного объема текучего тела) различают внешние и внутренние силы.

Внешние силы действуют между элементами этой системы (частями выделенного объема) и элементами, не относящимися к сис­теме. Такие силы могут вызывать изменение количества дви­жения и кинетической энергии выделенного объема. Пример внешней силы - сила тяжести.

Внутренние силы действуют между элементами ме­ханической системы (частями выделенного объема текучего тела). Они не могут изменить количества движения этого объема, так как внутри него каждая внутренняя сила уравновешивается равной ей по модулю внутрен­ней силой противоположного направления. Однако, работа внутренних сил может изменить кинетическую и (или) потенциальную энер­гию объема текучего тела. Примеры внутренних сил: сила давления, действующая на поверхность, построенную внут­ри выделенного объема жидкости; сила трения между слоями движущейся жидкости.

Применяя при изучении механики жидкости модель сплошной среды, различают объемные и поверхностные силы.

Объемные (массовые) силы пропорциональны объему (массе) жидкости, на который они действуют. Характеристика объемной силы - плотность распределениясилы в пространстве. Это векторная величина f = (f_x, f_y, f_z), которая равна силе, действующей на единицу объема (массы). Пример объемной силы - сила тяжести; плотность ее распределения представляют в виде силы, приходящейся на единицу массы сплошной среды. Если принять оси х и у горизонтальными, a z направить вертикально вверх, то плотность распреде­ления силы тяжести f_g = (0,0, -g), где g = 9,81 м/с² - ускорение свободного падения. Вес F_g объема V

Таким образом, вес тела направлен вниз (знак «-») и равен ρgV.

Массовые силы - сила тяжести и сила инерции - действуют на каждую частицу массы жидкости и поэтому пропорциональны его массе. Массовая сила характеризуется ускорением, сообщаемым ею единице массы.

Поверхностные силы пропорциональны площади поверхности, на которую они действуют. Пример такой силы - сила взаимодействия двух соприкасающихся слоёв жидкости, движутся относительно друг друга.

Характеристика поверхност­ной силы на заданной поверхности - плотность распределения (по поверхности), которую при использовании модели сплошной среды называют напряжением. Это векторная величина.

Напряжение в точке поверхности проектируют на нормаль к ней и на касательную плос­кость, выделяя при этом нормальные икасательные напряжения.

Поверхностные силы обусловлены силами ближнего взаи­модействия молекул, расположенных по разные стороны от рассматривае­мой поверхности, и переносом молекул сквозь эту поверхность в процессе их теплового движения. Это силы гидравлического давления (нормальные) и силы внутреннего трения (касательные).

Рассмотрим некоторый объем жидкости (рис. 2.1), находящийся в равновесии под действием сил Р₁, Р₂, …. Мысленно рассечём этот объем произвольно выбранной плоскостью АВСД и отбросим его верхнюю часть. Для сохранения равновесия нижней части приложим к плоскости АВСД силы, эквивалентные действию отброшенной части.

Пусть Р - равнодействующая сил воздействия верхней части объема на нижнюю. Эта сила приложена в точке a плоскости АВСД, площадь которой - ω. Отношение

Р/ω=р_ср

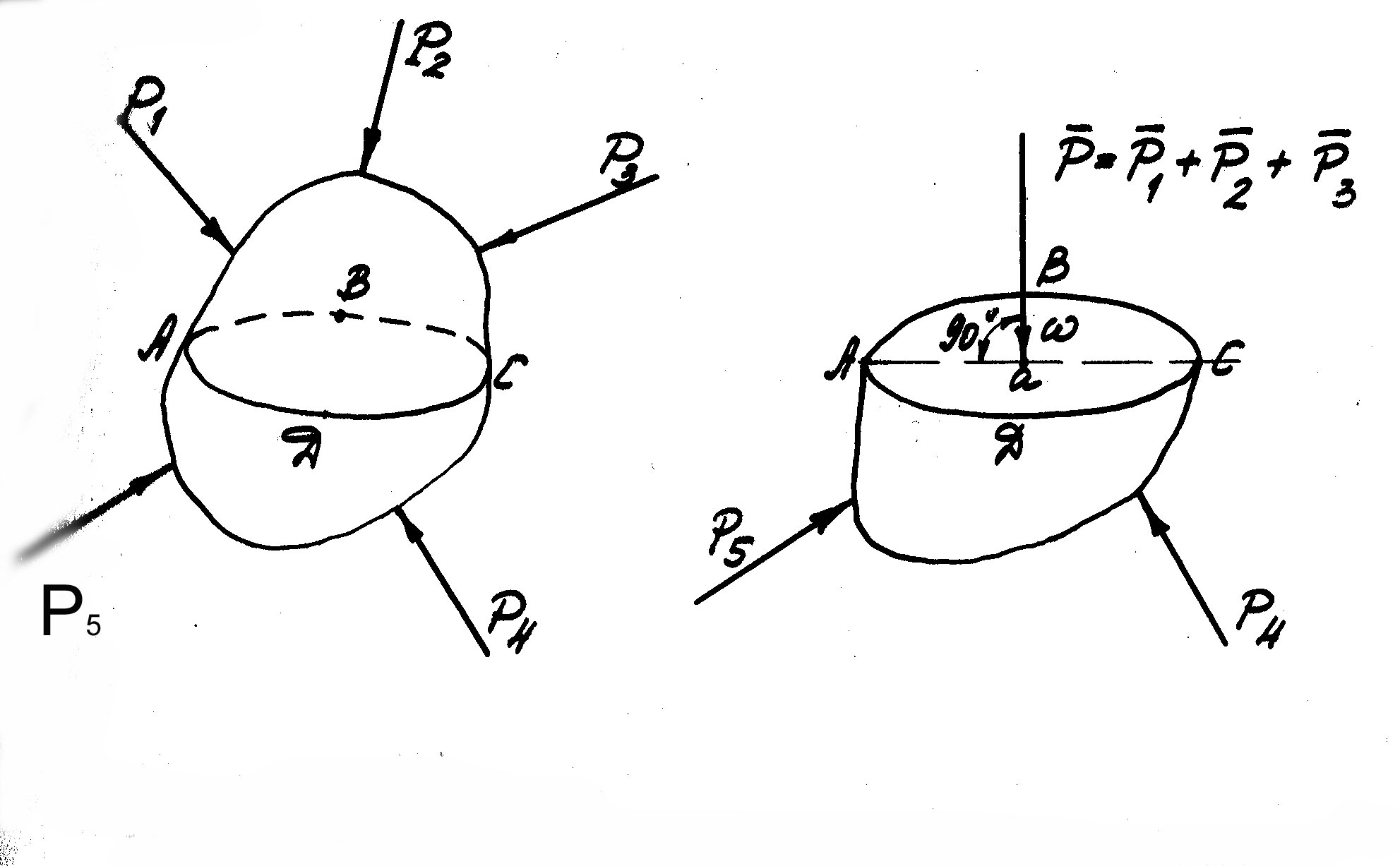Рис. 2.1

есть среднее гидростатическое давление на площадь ω или среднее гидростатическое напряжение давления. Если ω устремить к нулю, то отношение Р/ω устремится к пределу, выража-ющему давление в точке:

. (2.1)

Сила Р - общая сила давления на площадку (гидравлическая сила), р - гидростатическое давление в точке(просто гидростатическое давление).

В покоящейся жидкости касательные силы отсутствуют, поэтому гидростатическое давление - результат действия нормальных сжимающих сил, то есть поверхностных сил давления и массовых сил.

Гидростатическое давление имеет размерность напряжения: в системе МКГСС - кгс/м², в системе СИ - Н/м²; 1 Н/м² = 1 Па (Паскаль).

Гидростатическое давление идеальной жидкости обладает свойствами, распространяемыми и на давление реальных, но не очень вязких жидкостей:

1. Действует нормально к площадке, воспринимающей его, внутрь объема жидкости.

2. В любой точке жидкости не зависит от ориентации площадки, на которую оно действует, т. е. действует одинаково по всем направлениям.

3. Гидростатическое давление в точке зависит от ее положения в пространстве, занятом жидкостью, то есть давление - функция координат:

р =p(x, y, z). (2.2)