Формула Эйлера. Полное теоретическое давление, создаваемое колесом центробежного нагнетателя
Давление, развиваемое рабочим колесом центробежной машины, зависит от скорости потока, проходящего через колесо, и от его размеров. Впервые формула, позволяющая рассчитать это давление, была получена Л. Эйлером в 1754 г. Рассмотрим вывод этой формулы. Введем следующие предположения:1) поток состоит из множества струй, повторяющих геометрическую форму лопасти; 2) поток осесимметричен, т.е. все составляющие его струи геометрически и кинематически одинаковы; 3) течение является плоским, т.е. градиент скорости вдоль геометрической оси машины равен 0. Первые два предположения справедливы при бесконечно большом числе лопаток и при бесконечно малой их толщине.
Для вывода используем теорему количества движения (теорему импульсов), в соответствии с которой изменение количества движения секундной массы при переходе от одного сечения к другому равно сумме внешних сил, приложенных к потоку между этими сечениями. Обозначим сумму внешних сил через 
и получим
, (2.2)
где Lсек – объемный расход, м3/с.
Изменение момента количества движения секундной массы при переходе от одного сечения к другому равняется моменту внешних сил, приложенных к потоку между этими сечениями.
Уравнение моментов внешних сил имеет вид
, (2.3)
где l2, l1 - плечи скоростей C2, C1 относительно оси вращения, м.
Рассмотрим треугольники AOB и BDE, (рис.2.2), гипотенузами которых являются соответственно радиус вращения R и скорость C и катетами – плечо l и скорость Cu. Нетрудно заметить, что треугольники подобны.
Рис.2.2. К выводу формулы Эйлера
Поэтому
и Cl = CuR.
Тогда
.
Умножим обе части этого выражения на угловую скорость w и получим
.
Так как Мω=N (мощность), а Rω = u (окружная скорость), то
.
С другой стороны, 
. В результате получим
, (2.4)
где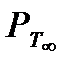 
– теоретическое давление, Па.
Это и есть формула Эйлера. Индекс ∞ в формуле означает, что зависимость (2.4) справедлива при бесконечном числе лопаток.
Введем понятие коэффициента закручивания потока
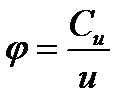. (2.5)
Тогда формула Эйлера примет вид
. (2.6)
Если к колесу подтекает незакрученный поток, т.е. C1u=0 и 
=0, то формула (2.6) примет вид
. (2.7)
Соответствующие выражения для напора имеют вид:
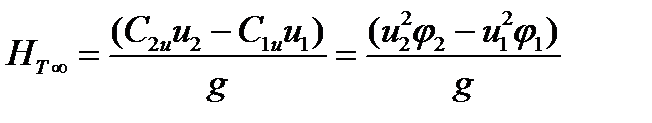, (2.8)
. (2.9)
Действительное давление, развиваемое колесом, меньше теоретического вследствие потерь энергии на гидравлическое сопротивление в проточной части нагнетателя и несоблюдения в реальных машинах принятых при выводе формулы Эйлера допущений.
Поэтому теоретическое давление определяется по формуле
, (2.10)
где μ<1 – поправочный коэффициент, учитывающий конечное число лопастей. Для ориентировочных расчетов μ»0,8.
Действительное давление вычисляется по зависимости
, (2.11)
где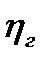 
– гидравлический КПД.
Формула (2.11) может быть представлена и в другом виде
, (2.12)
где 
– потери давления в нагнетателе.
Из вывода формулы Эйлера следует, что передача энергии жидкости происходит за счет изменения момента количества движения жидкости, проходящей через рабочее колесо. При этом остается неясным, из каких частей слагается переданная энергия. Для ответа на этот вопрос преобразуем формулу Эйлера с помощью зависимости между скоростями, следующей из параллелограммов скоростей:
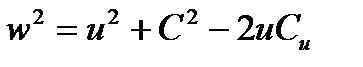. (2.13)
где w – направление скорости входа, м/с.
После подстановки значения uCu в формулу (2.4) получим
. (2.14)
Первый член уравнения выражает увеличение потенциальной энергии за счет работы сил вращения, второй – за счет увеличения площади для прохода жидкости в межлопаточном пространстве, третий член описывает возрастание кинетической энергии. Из этого уравнения следует вывод, что статическое давление, создаваемое нагнетателем равно
, (2.15)
а динамическое равно
. (2.16)