Теоретическая часть.
Лабораторная работа №1. Случайные события
«Классическое определение вероятности. Основные формулы комбинаторики».
Теоретическая часть.
Классическая схема позволяет вычислять вероятности без проведения случайного эксперимента, основываясь лишь на свойстве симметрии возможных исходов испытания, так что нет оснований считать какой-либо из исходов более вероятным, чем другой.
Определение: Вероятностью случайного события А, называется отношение числа m исходов, благоприятствующих событию А, к числу всех равновозможных исходов испытания, составляющих полную группу несовместных событий.
Р(А)=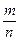 
При непосредственном подсчете вероятностей часто используют формулы комбинаторики. Простейшими из них являются перестановки, сочетания, размещения и разбиения.
Перестановки отличаются друг от друга только порядком входящих в них элементов. Количество перестановок из n элементов:
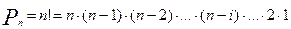
Пример 1: Сколькими способами можно рассадить 10 человек за круглым столом, если имеет значение только порядок соседей.
Отметим, что вращение людей вокруг стола не меняет их взаимного расположения, поскольку соседи справа и слева остаются прежними. Если место за столом уникально, то существует 10! Способов рассадить людей за столом. Существует 10 вращений вокруг стола, поэтому делим на 10 и получаем 9! Способов рассадить людей за круглым столом, если значение имеет только порядок соседей.
Пусть М – множество, состоящее из n элементов.
Размещением из n элементов по m или упорядоченной (n,m)– выборкой, называется любой кортеж, состоящий из m, попарно различных элементов множества М.
Число размещений из n по m элементов:
Пример 2: Сколько различных четырехзначных чисел можно образовать из цифр 1, 2, …, 9, если все цифры различны.
Существует
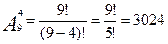
Сочетанием из n элементов по m или неупорядоченной (n,m)– выборкой, называется любое подмножество множества M, состоящее из m элементов.
Надо заметить, что количество сочетаний отличается от числа размещений количеством перестановок каждого сочетания, то есть
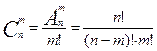
Пример 3: Сколько существует вариантов выбора 5 карт трефовой масти из колоды, состоящей из 54 карт.
В колоде имеется 13 треф, из которых выбирается 5, поэтому
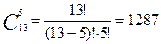
Пусть множество М разбито на k таких различных типов, что имеется n1 неразличимых объектов типа 1, n2 неразличимых объектов типа 2, и, вообще, ni неразличимых объектов типа i (i=1,2,3,…,k), тогда количество различных размещений элементов множества:
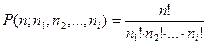
Пример 4: Сколькими способами можно расставить на полке 12 книг, из которых 4 одинаковых учебника по математике, 6 одинаковых по информатике, 2 одинаковых по химии.
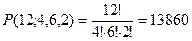
Если трактовать повторения как возвращения объекта во множество М и повторное его использование, то возникает идея размещений и сочетаний с повторениями. Их количество можно вычислить по формулам:
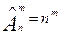– количество размещений из n элементов по m с повторениями.
– количество сочетаний из n элементов по m с повторениями.
Пример 5: Сколько различных четырехзначных чисел можно образовать из цифр 1, 2, …, 9.
Так как нет ограничения на повторение цифр, то существует
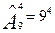
Теорема: Если необходимо выбрать хотя бы по одному объекту из n по m с повторением, то количество различных сочетаний равно
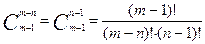
Пример 6: Если в булочной продается 10 видов различных пончиков, то сколькими способами можно выбрать 12 пончиков.
Поскольку 12 пончиков выбираются из 10 видов с повторениями, то
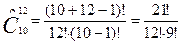
Пример 7: Если в булочной продается 10 видов различных пончиков, то сколькими способами можно выбрать 12 пончиков, если необходимо выбрать хотя бы по одному пончику каждого вида .
Поскольку 12 пончиков выбираются из 10 видов с повторениями, то
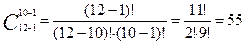
Пример 8: Найдем количество различных решений уравнения
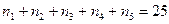, где каждое слагаемое в левой части – неотрицательное число.
Это эквивалентно вопросу о том, сколько существует выборок вида
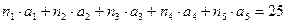, где имеется 
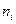объектов типа 
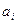и
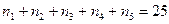, но количество таких выборок - это количество различных сочетаний из 25 элементов по 5 элементов с повторениями. Итак, существуют
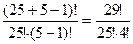
В среде MathCad нет встроенных функций для подсчета количества способов выбора объектов, поэтому необходимо воспользоваться возможностью программирования.
Чтобы создать программный модуль:
1. Введите выражение, которое будет находится слева от знака присваивания (имя функции);
2. Вызовите на экран панель Programming (программирование);
3. Нажмите на кнопку Add line[1] необходимое число раз;
4. В появившиеся местозаполнители введите необходимый программный код.
Для подсчета факториала необходимо организовать цикл. В среде MathCad это можно сделать с помощью оператора for и ранжирванной переменной, которая пробегает некоторое множество значений.
Фрагмент документа MathCad для подсчета факториала приведен ниже.
После того как программный модуль полностью определен и ни один из местозаполнителей ни остался пустым, функция может использоваться обычным образом.
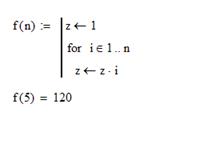
Пример решения задачи на подсчет вероятности в среде МathCad:
