Методика изучения нумерации чисел первого десятка

Главными задачами при проработке темы "Нумерация чисел первого десятка" есть:

а) дать ученикам представления о натуральном числе как числе, которое используется при счете;

б) раскрыть понятие последовательности числа в пределах 10 и принципов ее построения;

Изучение чисел первого десятка проходит монографическим способом, то есть каждое число изучается отдельно, и вместе с тем связано с понятиями построения последовательности натуральных чисел в пределах данного числа. Можно выделить следующие этапы:

· а) образование каждого числа;

· б) запись числа с помощью цифры;

· в) сравнение числа, которое изучается, с предыдущими;

· г) место числа в последовательности натуральных чисел;

· д) состав числа.

На первом этапе очень важно показать ученикам, что слова-числительные можно заменить математическими символами – цифрами(1,2,3 и т.д.). Это позволяет познакомить учеников с натуральным рядом чисел.

Для усвоения закономерности построения натурального ряда чисел(каждое число в натуральном ряду больше предыдущего и меньше следующего на 1), при изучении каждого нового числа учитель проводит однотипные упражнения. Например, при изучении числа в промежутке 1- 6 проводится серия таких упражнений :

5.Положите в строку три круга. Найдите карточку с цифрой, которая обозначает число три и положить ее рядом с кругами. Ниже положите треугольников столько, сколько кругов. Придвиньте еще один треугольник . Сколько стало теперь треугольников? Как мы получили четыре треугольника? Каких фигур больше: треугольников или кругов? На сколько больше? В строку с треугольниками положить карточку с цифрой, которая обозначает число четыре. Какое число больше четырех или три? На сколько больше?

6.Положите ниже квадратов столько, сколько треугольников. Сколько у вас есть квадратов? Что необходимо сделать, чтобы квадратов стало больше на 1, чем треугольников? Сколько стало теперь квадратов? Положите рядом с квадратами карточку с цифрой, которая обозначает число пять.

7.Как можно получить из числа три число четыре? Из числа четыре - число пять.

8.Какое из двух чисел можно назвать следующим: три или четыре? Четыре или пять? Как получить из числа 3 следующее число, и которое это число? Как получить из числа 4 следующее число, и которое это число? Какое из двух чисел можно назвать предыдущим: два или три? Четыре или пять? Как получить из числа пять предыдущее число, и которое это число? Какое число будет больше числа четыре на 1? Какое число будет меньше числа четыре на 1? Названию "соседей" числа 4.

9.Какие числа мы изучали на предыдущих уроках? (1,2,3,4,5). Какое число при счете мы называем после пяти? Как можно назвать число шесть по отношению к пяти? Как можно получить следующее число из предыдущего? Как можно получить число шесть из числа пять? Положіть в строку пять прямоугольников красного цвета. Что необходимо сделать, чтобы прямоугольников стали шесть? Присуньте один прямоугольник синего цвета. Под прямоугольниками красного цвета положіть карточку с цифрой, которая помечает число пять, а под прямоугольником синего цвета карточку с цифрой, которая помечает число один. Покажите карточку с цифрой, которая помечает число, которое указывает на общее количество прямоугольников. Назовите это число. Как получить из числа пять число шесть? Сложите из карточек с числами пример, который показывает, как из числа пять образовать число шесть.

10.За каким числом следует число шесть? Как образовать из числа шесть число пять? На сколько число шесть больше, чем число пять? На сколько число пять меньше, чем число шесть? Назови все числа, которые при счете называют раньше, чем число шесть. Названия все числа, которые меньше чисел шесть?

11.Какой знак можно поставить между числами 2 и 3? 2 и5? 4 и6? 6 и5? 6 и1?

Проводя упражнения на сравнение чисел, необходимо подвести учеников до двух правил, которые опираются на порядковую и количественную теорию чисел, :

а)число 6 больше при числе 1, 2, 3, 4, 5 потому, что при счете его называют последним в данном ряду чисел;

б)число 6 больше при числе 1, 2, 3, 4, 5 потому, что оно помечает большее количество предметов.

Образование обратной последовательности чисел опирается на операцию отчисления по единице. У детей шестилетнего возраста такая операция вызывает некоторые трудности. Если не показать ученикам практическую значимость такой операции, то цепочка слов числительных : 10, 9, 8 .,1 усваивается формально. Поэтому полезные, например, упражнения такого содержания :

 

На доске шесть домов. В процессе счета им присваиваются соответствующие номера. Почтальону необходимо доставить письмо в дом №4. Как это сделать быстрее, если он стоит у последнего дома? Вернуться к дому №1 и считать последовательно от одного до четырех, или начинать с дома №6 и отчислять дома в обратном порядке? Почему второй способ более рационален?

После обучения учеников записывать число с помощью цифры, изучается его состав сначала с помощью наглядности.

6 = 5 + 1 6 = 4 + 2

6 = 3 + 3 6 = 2 + 4

6 = 1 + 5

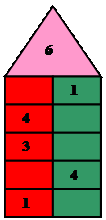
На следующем этапе ученики составляют таблицу состава числа и изучают ее наизусть. Для закрепления таблицы предлагаются разнообразные упражнения в игровой форме. Например, в форме сказки:

"Число 6 построило себе домик, и поселилось на самом верхнем этаже. Одиноко ему стало жить одному. Решило число 6 заселить весь домик, на каждом этаже которого по две квартиры. Но не любые числа могут стать соседями, а только те, которые вместе складывают число 6. Долго рассуждало число, как это сделать. Наконец, часть чисел оно оселило на этажах. Как же подобрать к ним соседей? Помогите числу 6".

 

Нумерация в концентре "Десяток" заканчивается темой "Число и цифра 0". Работа учителя должна подвести учеников к выводу, что числом 0 помечают отсутствие предметов#00в множестве, то есть являются характеристикой пустого множества. Прием изучения связан из установления соответствия между фигурой числа, числом, которое помечает количество предметов, и цифрой :

 

 

 

4 3 2 1 0

Методика изучения нумерации чисел в концентре "Сотня"

3.1. Изучение чисел второго десятка

Изучение нумерации чисел в пределах 100 делится на два этапа: в первом классе изучают числа от 11 до 20, во втором - все числа в пределах 100. Такое деление в концентре "Сотня" обусловленно тем, что многие первоклассники умеют считать числа до 20. Но главная причина в том, что название слов числительных второго десятка отвечает одной закономерности (сначала называется количество единиц, а потом называется десяток - дцать), у записи чисел 11 - 20 прослеживается другая закономерность: сначала пишем цифру, которая помечает один десяток, а потом цифру единиц.

Сначала изучается устная нумерация, то есть ученики усваивают название чисел, а потом письменная. Для того, чтобы ученики хорошо усвоили тему, учитель должен широко использовать наглядность: счетные палочки, абаки, нумерационные полоски.

На первом этапе формируется понятие о десятке как счетной единице. Начинать можно из задания: "Белочка насобирала на зиму полную корзину грибов. (Например - 36 грибов.) Хочет их посчитать, но она может считать только до 10. Долго белочка думала, но смогла все же посчитать все грибы. Кто догадался, как она это сделала"?. Ученики, выходя к доске, предлагают свои способы. Наконец догадываются, что можно отсчитать сначала 10 грибов, потом - еще 10 и еще 10. Остается еще 6 грибов. Получили три кучки по 10 грибов и еще 6 грибов. Учитель знакомит детей с понятием десяток, объясняет, что грибов три десятка и еще 6 отдельно. Потом проводится работа со счетными палочками.Отсчитывая по десять палочек и завязывая их в связки, ученики узнают, что десять единиц образуют один десяток. Потом переходят к счету десятками: один десяток, два десятка ., десять десятков. Такие упражнения подводят детей к выводу, что десятки можно считать как простые единицы.

Чтобы у учеников не сложилось представление, что только связки палочек можно называть десятками, учитель предлагает детям вспомнить, какие предметы считают десятками. В конце делается обобщающий вывод: любые десять предметов образуют десяток, а число десять имеет еще другое названидесяток.

На втором этапе учеников знакомят с образованием чисел от 11 до 20 (знакомым им способом: причислением к предыдущему числу единицы, и отчислением от следующего числа единицы), названием чисел. Причем, название чисел можно продемонстрировать на палочках: одну палочку(один) кладем на десять(дцять), проговорюємо: один-на-дцять и так далее. Ученики управляются в порядковом и обратном счете чисел в пределах 20, проводят операцию сравнения

На третьем этапе переходят к письменной нумерации чисел, обращая внимание на то, что очень важное значение имеет место, на котором мы записываем соответствующие цифры. Эта работа начинается со знакомого уже ученикам числа 10.

Беседу с учениками можно провести за такими вопросами: "Я называю число(например, число 8). Покажите, с помощью какой цифры мы можем записать это число", "Сколько нам нужно цифр, чтобы записать число 8"?, "Сколько нужно цифр, чтобы записать число 9? Покажите эту цифру"; "Покажите цифру, с помощью которой мы можем записать число 0"; "Сколько понадобитесь цифр, чтобы записать число 0"; "Какое число я показываю"?; "Покажите цифры, с помощью которых мы можем записать число 10"; "Сколько понадобитесь цифр, чтобы записать число 10"?. Делается вывод, что для записи чисел от одного до девяти и числа 0 нужно по одной цифре, а для записи числа 10 необходимо использовать две цифры.

Дальше работа проводится с нумерационными лентами.

Сколько кружочков изображено на ленте красного цвета? (10 - один десяток);

Сколько кружочков на ленте зеленого цвета(2 - две единицы)

Какое число получаем если к одному десятку прибавить две единицу? (12).

Покажите цифру, которая указывает на количество десятков в числе 12. Покажите цифру, которая указывает на количество единиц в числе 12.

 

Для записи числа 11 необходимо записать и количество единиц, и количество десятков, поэтому какие цифры нам нужно записать? Сколько цифр? (Учитель записывает на доске число 11 и поясняє, что цифра слева указывает на количество десятков, то есть один десяток, а цифра 1 дело - на количество единиц, то есть одна единица.) Ученики записывают число 11 и еще раз объясняют позиционное значение цифры 1.

Аналогичная работа проводится с другими числами. Вводится понятие однозначные и двузначные числа.

На четвертом этапе учеников знакомят с понятиями разрядные единицы, разряд десятков, разряд единиц, а также с образованием чисел из десятка и единиц. Предлагаются такие упражнения с использованием абаков разных конструкций :

 

 

т из одного десятку и двух единиц. Запипока

шите это число.

 

Покажите на абаке число 15. Сколько в этом числе десятков? Сколько единиц?

Покажите на абаке число, в котором в разряде единиц шесть разрядных единиц, а в разряде десятков одна разрядная единица. Запишите это число.

Запишите число 18 в виде суммы разрядных единиц( 18 = 10 + 8).

Есть сумма разрядных единиц : 10 + 3. Какое число образует эта сумма? (10 + 3 = 13).

3.2. Изучение чисел от 21 до 100.

Числа от 21 до 100 изучаются во втором классе с начала учебного года. Но этот промежуток числа не отделяется и является продолжением последовательности натуральных чисел 1 - 100. Методические приемы, что использует учитель на этом этапе такие же, как и при изучении чисел первого и второго десятков.

Сначала изучается устная нумерация, потом - письменная.

В результате изучения нумерации чисел в концентре "Сотня" и проведение соответствующих упражнений, ученики должны хорошо знать названия чисел в данном промежутке, записывать и читать их; осознавать позиционное значение цифры в записи двоцифрових чисел, десятичный состав числа из десятков и единиц; понимать понятие разряд, единицы первого и второго разряда.

Новые знания из нумерации чисел в промежутке от 21 до 100 полностью базируются на предыдущих знаниях и умениях учеников.

Особое внимание следует уделять значению цифры 0 у записи чисел. В счете круглых десятков не называют единиц, но это не значит, что разряд единиц отсутствует. Учитель может провести такую беседу: "Сколько в числе 30 единиц в первом разряде? Посмотрит на щепотки палочек. Имеем ли мы отдельные палочки, то есть отдельные единицы? Какой цифрой обозначается число, которое указывает на отсутствие любых предметов? Какую же цифру нам надо записать в разряде единиц? Помечает ли цифра 0 отсутствие разряда единиц в числе 60? Отсутствие чего помечает цифра 0 в числе 50"?.

На данном этапе изучения нумерации широко используют упражнения, которые направлены на умение представлять двузначные числа в виде суммы разрядных слагаемых и наоборот, :

78 = 70 + 8; 80 + 5 = 85.

Важно также довести до ума детей разницу между понятиями разрядные единицы в числе и количеством единиц, из которых вообще состоит число. Так в числе 52 всего 52 единицы, в разряде единиц - 2 единицы. В этом же числе 5 десятков. При этом важно использовать нумерационные ленты.

Ученики наглядно видят, что в числе 52 действительно 52 единицы(всего 52 кружка); вместе с тем пять полосок по десять кружочков образуют пять десятков - цифра 5 записывается во втором разряде; отдельных единиц - две, цифра 2 записывается в первом разряде.

 

 

 

Систематизируя знания учеников о нумерации чисел в пределах 100, учитель предлагает детям предоставлять полную характеристику любому числу. Например, характеризуя число 66 ученики должны: называть общее количество единиц (66 единиц); десятичный состав(в этом числе 6 десятков и 6 единиц; 6 единиц второго разряда и 6 единиц первого разряда); определить место числа в натуральном ряде (число 66 называют во время счета после 65 и перед 67); выделить особенность записи числа ( 66 - число двузначное, для его записи использована дважды цифра 6).