Средняя гармоническая
Средняя гармоническая может быть простой и взвешенной. Простая средняя гармоническаярассчитывается по формуле:
r w:val="000000"/><w:sz w:val="32"/><w:sz-cs w:val="32"/><w:lang w:val="EN-US"/></w:rPr><m:t>X</m:t></m:r></m:e></m:bar></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
= 
. (3.4)
где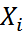 
— индивидуальное значение признака (варианта);
n — объем совокупности (число единиц совокупности).
Средняя гармоническая взвешеннаяпри меняется вместо средней арифметической взвешенной, когда нет данных о частотах отдельных вариант (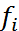 
) совокупности, но есть данные о величине произведения – 
.
Средняя гармоническая взвешенная рассчитывается по формуле
r w:val="000000"/><w:sz w:val="32"/><w:sz-cs w:val="32"/><w:lang w:val="EN-US"/></w:rPr><m:t>X</m:t></m:r></m:e></m:bar></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> = 
, (3.5)
где 
.
Cредняя гармоническая является преобразованной формой средней арифметической и тождественна ей (cм. (3.3)).
Использование одной из двух названных средних в каждом конкретном случае определяется характером имеющейся информации. Вместо средней гармонической всегда можно рассчитать среднюю арифметическую, для чего следует определить веса средней арифметической 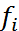, скрытые в весах средней гармонической 
.
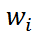Рассмотрим пример.Имеются данные о работе трех обменных пунктов валюты за день (табл. 3.4).
Таблица 3.4 – Валютный курс в обменных пунктах банка
| Обменный пункт | Курс доллара, руб./долл. | Объем продаж, тыс. долл. | Выручка от продажи валюты, тыс. долл. |
| – | 
| 
| 
|
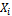
| №1 | 28,70 | 2,3 | 66,01 |
| №2 | 28,68 | 10,4 | 298,27 |
| №3 | 28,75 | 1,5 | 43,12 |
| Итого | х | 14,2 | 407,40 |
Первый вариант.По каждому обменному пункту известен валютный курс доллара (графа 1) и объем продаж долларов (графа 2).
Второй вариант.По каждому обменному пункту известен валютный курс доллара (графа 1) и выручка от продажи валюты (графа 3).
Требуетсяопределить средний взвешенный курс доллара но трем обменным пунктам банка.
Запишем формулу, по которой определяется курс доллара:
Если воспользоваться данными первого варианта, то средняя арифметическая взвешенная курса доллара будет выглядеть следующим образом:
При использовании данных второго варианта (графы 1, 3) числитель будет суммой выручки от продажи долларов по каждому обменному пункту (66,01+298,27+43,12) тыс.руб. Для нахождения общего объема продаж сначала необходимо рассчитать его по каждому обменному пункту по формуле
В итоге средний курс доллара будет определяться так:
В этом случае была использована средняя гармоническая взвешенная.
Результаты расчетов тождественны и выбор вида средней был обусловлен только имеющейся информацией.
Общее правило формулируется следующим образом.При расчете среднего уровня признака, представляющего собой относительную величину, используются средние взвешенные: арифметическая и гармоническая. Выбор вида средней в каждом конкретном случае определяется имеющейся информацией. Если имеется информация о знаменателе формулы, по которой определяется усредняемый признак, то используется средняя арифметическая. Если же имеется информация о числителе этой формулы, то используется средняя гармоническая.