Задачи, приводящие к дифференциальным уравнениям. Дифференциальные уравнения первого порядка. Изоклины. Задача Коши. Теорема существования и единственности задачи Коши.
Уравнения, в которые неизвестная функция входит под знаком производной или дифференциала, называются дифференциальными уравнениями. Подобными уравнениями описываются многие физические явления и процессы.
Примеры.
1) 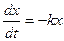 - уравнение радиоактивного распада ( k – постоянная распада, х – количество неразложившегося вещества в момент времени t, скорость распада
- уравнение радиоактивного распада ( k – постоянная распада, х – количество неразложившегося вещества в момент времени t, скорость распада 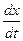 пропорциональна количеству распадающегося вещества).
пропорциональна количеству распадающегося вещества).
2)  - уравнение движения точки массы т под влиянием силы F, зависящей от времени, положения точки, определяемого радиус-вектором r, и ее скорости
- уравнение движения точки массы т под влиянием силы F, зависящей от времени, положения точки, определяемого радиус-вектором r, и ее скорости 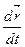 . Сила равна произведению массы на ускорение.
. Сила равна произведению массы на ускорение.
3)  - уравнение Пуассона, задающее зависимость между многими физическими величинами. Например, можно считать, что u(x,y,z) – потенциал электростатического поля, а ρ(x,y,z) – плотность зарядов.
- уравнение Пуассона, задающее зависимость между многими физическими величинами. Например, можно считать, что u(x,y,z) – потенциал электростатического поля, а ρ(x,y,z) – плотность зарядов.
Мы будем рассматривать уравнения, где неизвестная функция является функцией одной переменной. Такие уравнения называются обыкновенными дифференциальными уравнениями.
Определение 16.1. Уравнение вида
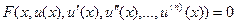 (16.1)
(16.1)
называется обыкновенным дифференциальным уравнением п-го порядка. При этом порядком уравнения называется максимальный порядок входящей в него производной.
Определение 16.2. Функция, которая при подстановке в уравнение (16.1) обращает его в тождество, называется решениемдифференциального уравнения.