Графическое представление результатов

В большинстве случаев экспериментального исследования различных физических явлений целесообразно представить полученные результаты в виде графика. Как оценить, согласуются ли результаты опыта с ожидаемой величиной, получаемой из зависимости между измеряемыми величинами? Наглядное представление об этом получают, сопоставляя теоретическую кривую и найденные экспериментально точки. Особенно удобно, например, проверять, ложатся ли данные точки на прямую линию. Поэтому при построении графиков желательно выбрать такие координаты, чтобы ожидаемая зависимость была линейной. Например, при определении ускорения свободного падения из соотношения 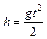между высотой и временем падения удобно строить график в координатах . 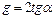Тогда ( – угол наклона прямой к оси ОХ), т. е. 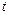определяется по всей совокупности результатов измерений и 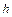. Чтобы изобразить графически зависимость одной физической величины от другой в прямоугольной системе координат, на ось абсцисс наносят шкалу значений аргумента, а на ось ординат – шкалу значений функции. Масштабы для аргумента и функции должны быть удобными и обязательно то, чтобы одна клетка графика соответствовала (1,2,5)×10^k единицам измеряемой величины (k – целое число). Значения, соответствующие экспериментальным точкам, на осях не проставляются. Начало отсчета графика не обязательно должно соответствовать X=0 и Y=0. При выборе начала отсчета следует руководствоваться тем, чтобы экспериментальные точки занимали все поле графика. При проведении плавной кривой по экспериментальным точкам необходимо следить за тем, чтобы на каждом достаточно большом её участке точки располагались как выше, так и ниже кривой. Нельзя соединять последовательно все экспериментальные точки, т.к. ломаная не соответствует истинной физической зависимости (при повторной серии измерений эта линия не воспроизводится).

При построении графика можно «на глаз» достаточно точно провести лишь прямую линию. При этом надо следить, чтобы сумма отклонений точек, лежащих по одну сторону от прямой примерно равнялось сумме отклонений по другую сторону. Поэтому функциональную зависимость стараются часто представить линейной, тогда графиком будет прямая, не обязательно начинающаяся от начала координат.

Экспериментальные точки на графике представляют в виде крестиков, размах по высоте и ширине которых равен удвоенным погрешностям измерений, отложенных по осям величин.

Более подробная классификация погрешностей измерений, их расчет, правила построения графиков и работы с ними приведены в учебно-методическом пособии Е. А. Маниной и Г. А. Шадрина «Обработка результатов измерений физического практикума», Изд-во СурГУ, 2007 г.

Контрольные вопросы

1. Какие измерения являются прямыми, косвенными?

2. Что называется результатами измерения?

3. Что такое абсолютная и относительная погрешности?

4. Чем вызвано появление погрешностей измерения?

5. Что такое случайная погрешность, систематическая погрешность?

6. Что называется доверительной вероятностью, доверительным интервалом?

7. Как находится полуширина доверительного интервала (полная абсолютная погрешность среднего арифметического) измеряемой величины в серии прямых измерений, в серии косвенных измерений?

8. Как записать окончательный результат серии прямых и косвенных измерений?

9. Сколько значащих цифр следует приводить в погрешности? Какие цифры числа называются значащими?

10. Каковы правила действия с приближенными числами?

11. Как и зачем результаты представляются в виде графика?