Пример 3.

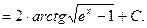
Пример 4.Найти  .
.
Решение. Пусть  .
.  .
.

Подставляя в исходный интеграл выражения его частей через t, получим:
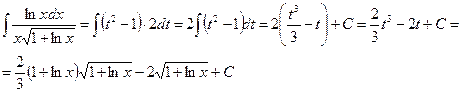
При сведении данного интеграла к табличному часто приходится использоватьинтегрирование подведением под знак дифференциала. Данный способ очень простой в своей основе, позволяет приводить интеграл к табличному, используя свойство инвариантности формул интегрирования, независимо от того, что является переменной интегрирования - независимая переменная х или функция U(х),т.е. если ∫f(x)dx=F(x)+C, то ∫f(U)dU=F(U)+C.
Таблица подведения функций под знак дифференциала
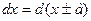
| 
| 
| |||

| 
| 
| |||
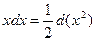
| 
| 
| |||
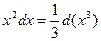
| 
| 
| |||
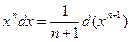
| 
| 
| |||
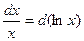
| 
| 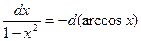
| |||

| 
| 
|
Пример 1.Найти  .
.
Решение. 
Пример 2.Найти  .
.
Решение.

Пример 3.Найти 
Решение. 
Пример 4. Найти
Решение. 
Пример 5. Найти 
Решение. 