Ранг матрицы

 

Определение 5.1. Для любой прямоугольной матрицы наивысший порядок отличных от нуля миноров называется рангом этой матрицы и обозначается через 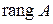(или ).

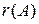Таким образом, если ранг матрицы равен 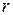, то среди миноров этой матрицы есть, по крайней мере, один минор 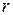-го порядка, отличный от нуля, в то время как все её миноры порядка 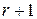и выше равны нулю.

 

Определение 5.2. Элементарными преобразованиями матрицы 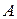называются следующие ее преобразования:

1) транспонирование;

2) перестановка двух строк или двух столбцов;

3) умножение всех элементов строки или столбца на любое число 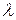, отличное от нуля;

4) прибавление ко всем элементам строки или столбца соответствующих элементов параллельного ряда, умноженных на одно и то же число.

 

Теорема 5.1. (об элементарных преобразованиях). При элементарных преобразованиях матрицы ее ранг не меняется.

 

Определение 5.3. Прямоугольная матрица называется ступенчатой, если выполняются следующие два условия:

1) после нулевой строки (то есть строки, состоящей только из нулей) располагаются только нулевые строки;

2) левее и ниже первого отличного от нуля элемента любой строки располагаются только нули.

 

Например,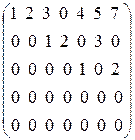

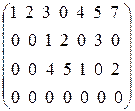
ступенчатая матрица неступенчатая матрица

Теорема 5.2.Любую ненулевую прямоугольную матрицу путем конечного числа элементарных преобразований можно привести к матрице ступенчатого вида. При этом ранг исходной матрицы будет равен числу ненулевых строк полученной ступенчатой матрицы.

Замечание. Данная теорема даёт возможность определять ранг любой прямоугольной матрицы.

 

Пример 1. Определить ранг матрицы

.

 

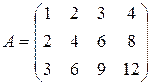Решение. Элемент 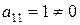, а все миноры второго и третьего порядков, содержащие этот элемент:

,

,

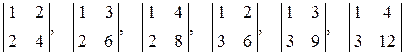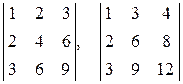как определители, имеющие пропорциональные строки (столбцы), равны нулю. Следовательно, .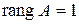

Определим ранг данной матрицы другим способом. Вычтем из второй строки удвоенную первую, а из третьей – утроенную первую. В результате получим матрицу

.

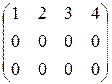Она является ступенчатой с одной ненулевой строкой. Следовательно, в силу теоремы 5.2 .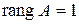

 

Пример 2. Определить ранг матрицы

.

 

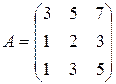Решение. Левый верхний минор второго порядка отличен от нуля:

,

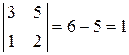а минор третьего порядка, окаймляющий его, то есть определитель самой матрицы, равен нулю:

.

 

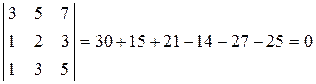Следовательно, .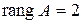

Вычислим ранг рассматриваемой матрицы путём приведения её к ступенчатой матрице. Поменяв местами первую строку со второй и вычитая после этого из второй строки утроенную первую, из третьей – первую, а затем прибавляя к третьей строке вторую, последовательно получаем

 

.

 

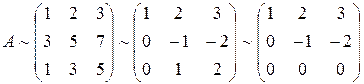Число ненулевых строк в последней матрице равно двум. Следовательно, в силу теоремы 5.2 .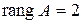

 

Пример 3. Вычислить ранг матрицы

 

.

 

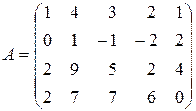Решение. Приведём матрицу 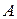к ступенчатому виду, для чего вычтем из третьей строки четвертую, а из четвертой – удвоенную первую. Тогда матрица перейдет в матрицу

 

.

 

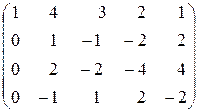Прибавим к последней строке вторую, а к третьей строке прибавим удвоенную четвертую. В результате получим матрицу

 

.

 

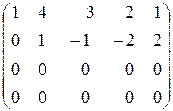Она является ступенчатой с двумя ненулевыми строками. Следовательно, .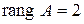

ЗАДАЧИ

 

1.13. Привести матрицу к ступенчатому виду и найти её ранг:

;	;	;
;	;	.

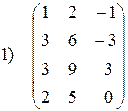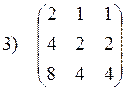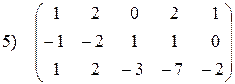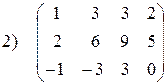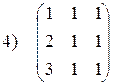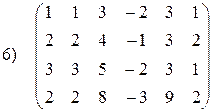1.14. Вычислить ранг матрицы обоими способами, рассмотренными выше:

1) 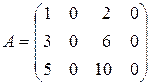;	3) ;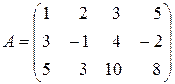
2) 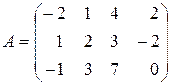;	4) 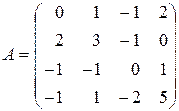.