Лекція 6. Нумерації. Канторові нумерації.

План:

1.Означення нумерації. Гьодельові та канторові нумерації.

2.Теорема про примітивну рекурсивність координатних функцій.

3.Приклади нумерацій.

4. Означення функції Гьоделя. Теорема про основну властивість функції Гьоделя.

Література:[3], [9], [10], [11].

Поняття МНР, ПРФ, РФ та ЧРФ введені нами на множині натуральних чисел N. Щоб перенести ці поняття на інші множини, елементи яких можуть мати досить складну будову (наприклад, множини функцій, термів і т.п.), будемо кодувати елементи цих множин натуральними числами. Введемо в розгляд поняття нумерації.

Нумерацією множини будемо називати функціональне відображення всієї множини N на множину . Це означає, що кожний елемент b 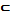має номер із N (можливо, не єдиний), але кожний елемент n 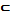N є номером єдиного елемента (п) .

Взаємно-однозначне відображення N на множину називають однозначною нумерацією множини .

В теорії алгоритмів особливий інтерес викликають гьодельові (або ефективні) нумерації, які дозволяють за кожним b 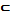ефективно (тобто за допомогою деякого алгоритму) визначити його номер, та за кожним n 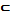N ефективно визначити той елемент (п) = b 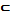, який нумерується цим n.

Більш строго, нумерація :N→ . називається гьодельовою, якщо

існує пара алгоритмів α та β таких що :

1) для кожного b 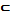, α(b) ^-1(b);

2) для кожного n 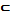N, β(n)= (n).

Спочатку розглянемо нумерацію пар та n-ок натуральних чисел, яку називають канторовими. Канторові нумерації є однозначними гьодельовими нумераціями.

Введемо у розгляд канторові нумерації послідовно для випадку n=2 і для довільного n. Для випадку n=2 всі пари натуральних чисел розташуємо у впорядковану послідовність наступним чином: будемо вважати, що пара (x,y) знаходиться в ній раніше за пару (u,v), якщо x+y<u+v, або, якщо x+у =и+v та х<u:

(0,0);

(0,1); (1,0);

(0,2); ( 1,1); (2,0);

(0,3); (1,2); (2,1); (3,0);…

(0,n); (1,n-1); (2,n-2);...,(n,0).

Номер пари (х,у) в такій послідовності позначають С(х,у) і називають канторовим номером пари (х,у). Наприклад, С(0,0)=0, С(0,2)=3. Ліву та праву компоненти пари з номером n позначають відповідно l(n) та r(п). Наприклад, l(4) = 1, r(3) = 2.

Функції l(n) та r(n) називають, відповідно, лівою та правою координатними функціями . Функцію С(х,у) називають функцією канторового номера.

Теорема. Функції С(х,у), l(n) та r(n) є примітивно рекурсивними функціями.

Доведення.

Справді, пара (х,у) знаходиться на х-му місці після пари (0,x+y). Перед парою (0,x+y) знаходиться х+у груп пар із однаковою сумою компонент, причому у групі із сумою компонент m міститься m+1 пара. Тому перед парою (0,х+y) знаходиться всього

n =1+2+...+ (х+у)=(х+у+1)·(х+у)/2 пар. Звідси С(х,у)=n+x , тобто С(х,y)=[(x+y+1)·(x+y)/2]+х=[((x+y)²+3·x+у)/ 2] є ПРФ.

Нехай х=l(n), у=r(n). Маємо 2 n=2 С(х, у)=(х+у )²+3 х + у, тому 8·n+1=(2·х+2·y+1)²+8·х=(2·x+2·y+3)²–8y–8. Звідси одержуємо 2·х+2·у+1 [ ]<2·х+2·у+3,aбo х+у+1 [([ ]+1)/2]<х+у+2. Отже, х+y+1=[([ ]+1)/2]. Але n=С(х,у)=[{х+у+1)·(x+y)/2]+х, звідки маємо, що функція

l(n)=х=n÷[(х+у+1)·(х+у)/2]=

=n÷[[([ ]+1)/2]/2] [[([ ]-1)/2]/2]- є ПРФ.

Тепер для правої координатної функції r(n).

r(n)=у=(х+у+1)÷(x+1)=[([ ]+1)/2]÷(х+1)=

=[([ ]+1)/2]÷(l(n)+1)-ПРФ

Функції С(x,y), l(n), r(n) зв'язані наступними тотожностями:

1. С(l(n),r(n))=n;

2. l(C(х,у))=х;

3. r(С(х,у))=у.

Маючи нумерацію пар натуральних чисел (випадок n=2), для довільного n можна узагальнити канторову нумерацію n-ок натуральних чисел таким чином:

C³(х₁,х₂,х₃) = С(С(х₁, х₂),х₃);

C^k+1 (х₁,х₂,…,x_k+1)=C^k(C(х₁, х₂),x₃,…,x_k+1) для к>2.

Якщо Cⁿ (х₁,...,х_n) = т, то координатні функції С_n1,...,C_nп вводимо наступним чином:

С_n1 (m)= x₁; С_n2 (m) = х₂;...С_nn (m) = х_n.

Для функцій Cⁿ, С_n1,..., С_nn маємо такі тотожності:

Cⁿ⁽C_n1(x),..,Сnn(х)) = х;

Сnj(Сⁿ(x₁,…,x_n)) = x_j ,1≤ j≤ n.

Теорема. Функції Cⁿ, С_n1,...,С_nn є ПРФ.

Доведення. Справді, маємо

Cⁿ(х₁,х₂,...,х_n) = C(...С(С(х₁, х₂),х₃),...,x_n)

С_nn (m) = х_п = r(m); С_{n n-1}(т) = х_п-1 = r(l(m));...

С _n2 (m) = x₂= r(l…l(m))..);С_n1 (m) = x₁,= 1(1..1(т)..).

Враховуючи такі представлення цих функцій і результати попередньої теореми робимо висновок що ці функції є ПРФ.

Функція Гьоделя дозволяє кодувати одним натуральним числом довільну скінчену послідовність натуральних чисел.

За визначенням функція Гьоделя,яка має вигляд

Г(x,y)=mod(l(x)), 1+(y+1)r(x))

є примітивно рекурсивною.

Справедлива наступна теорема.

Теорема. (про основну властивість функції Гьоделя) Для довільної скінченої послідовності натуральних чисел b₀ ,b₁ …,b_n , знайдеться натуральне число t таке, що Г(t,i)= b_i i=0…n.

Доведення теорема суттєвим чином опирається на лему.

Лема.Для довільної скінченої послідовності натуральних чисел b₀ b₁ …b_n і для довільних взаємно простих чисел p₀ ,p_{1 ,}…,p_n таких p_i< bi i=1,…,n знайдеться натуральне число M таке, що М< p₀ p₁ …p_n для якого виконується

mod(M, p_i)= b_i i=0…n.

Лему доводимо методом від супротивного.

Лекція 7. Гьодельові нумерації формальних моделей алгоритму.

План:

1. Алгоритми гьоделевих нумерацій МНР.

2. Алгоритми гьоделевих нумерацій машин Тьюрінга.

Література:[1], [6], [9], [10], [11].

Однозначну гьодельову нумерацію МНР задамо в два етапи.

На першому етапі кожну МНР-програму, яка складається із n команд кодуємо нумерацією µ, що утворює послідовність натуральних чисел за наступною схемою

µ (Z(n))=4n;

µ(S(n)) = 4n+1;

µ(T(m,n))= 4•С(m,n)+2.

µ(J(m,n,q))= 4•С(C(m,n),q)+3

За побудовою нумерація µ є бієктивним відображенням множини N на множину усіх команд МНР.

На другому етапі задамо однозначну гьодельову нумерацію v всіх скінчених числових послідовностей натуральних чисел наступним чином:

v(а₁,а₂,...,а_n)=2^a1+2^а1+а2+1+ ... + 2^{а1+а2+…+аn+n-1} -1.

Так як обидві нумерації, за побудовою, є однозначними, гьодельовими, то і їх композиція є однозначною гьодельовою нумерацією.

Гьодельову нумерацію всіх МТ задамо на основі кодування МТ. Кожну МТ можна задати послідовністю її команд такою, що перша команда містить в лівій частині q₀ остання команда містить в правій частині q*. Множину команд МТ можна впорядкувати у вигляді послідовності із вищевказаною властивістю багатьма способами, тому наша нумерація МТ неоднозначна. Домовимося впорядковувати команди (нумерувати ) МТ зліва направо по рядкам. Фінальний стан q* будемо позначати числом на одиницю більшим від номер останнього робочого стану.

Занумеруємо внутрішні стани МТ та символи стрічки:

Q = {q₀ ,…,q_n},Т = {а₀ ,...,а_m).

Кодування команд МТ задамо так:

µ= (q_ia_j →q_ka_lS)=3•C⁴ (i, j, k, l);

µ(q_ia_j → q_ka_l L) = 3•С⁴(i, j, k, l)+1;

µ(q_ia_j → q_ka_l R)= 3•С⁴(i, j, k, l)+2.

Таке кодування μ є бієктивним відображенням множини всіх можливих команд МТ на N. Використовуючи наведене вище кодування v: N^k →N, визначимо код машини Тьюрінга М, яка задана послідовністю команд I₁,…,I_k, таким чином : ρ(m) = v(μ(I₁ ,I₂ ,…,I_k)). Але μ та v бієктивні, тому ρ теж бієкція. Тоді φ = ρ^-1 - однозначна нумерація послідовностей команд МТ, але неоднозначна нумерація всіх МТ. Неважко переконатись, що така нумерація гьодельова.

Основна література до курсу:

1. Алферов З.В. Теория алгоритмов. М. Статистика, 1973-164с.

2. Мальцев А.И. Алгоритмы и рекурсивные функции. М.:Н.1986-367с.

3. Марков А.А., Нагорный Н.М. Теория алгоритмов. М.: Н.1984-423с.

4. Поляков Е.А., Рабинос М.Г. Теория алгоритмов. Учебное пособие по с/к для студентов математиков.1976-88с.

5. Арсланов М.М. Рекурсивно перечислимые множества и степени неразрешимости. Казань, 1986-44с.

6. Варпоховский Ф.Ф. Элементы теории алгоритмов. М.: Просвещение,1970-44с.

7. Кожевникова Г.П. Теория алгоритмов. Львов: Вища школа.1978-98с.

8. Лавров И.И. , Максимова Л.Л. Задачи по теории множеств и математической логике, теории алгоритмов. М.: Н.1984-224с.

9. Лавров И.И. Логика и алгоритмы. Новосибирск. 1970-173с.

10. В.В. Зубенко, С.С. Шкільняк. Теорія алгоритмів у прикладах і задачах. К.:1993-99с.

11. Ю.В. Нікольській, В.В. Пасічник., Ю.М. Щербина Дискретна математика. Львів.:2005-607с.