Методические указания

Обработка статистических данных совершается на основании положений теории вероятностей.

Теория вероятностей, вводя понятие вероятности случайного события, дает способ измерять числом степень возможности его осуществления и указывает приемы для определения этого числа. При этом теория вероятностей не может предсказать исход единичного события. Значение выявленных с помощью теории вероятностей закономерностей массовых явлений состоит в том, что они позволяют предвидеть, как эти события будут протекать в дальнейшем.

Случайной величиной называется числовая характеристика, связанная с изучаемым объектом, значение которой принципиально не может быть предсказано точно в зависимости от случая.

Формально случайная величина Х – это числовая функция, заданная на некотором вероятностном пространстве (Ω,Р): Х(ω), ωÎΩ. Функцией распределения случайной величины Х называется числовая функция числового аргумента, определяемая равенством F(x)=P(X£x), xÎR (R – множество действительных чисел). Каждая функция распределения обладает следующими свойствами:

ü 0£F(x)£ 1 при любом xÎR;

ü F(x)является неубывающей, непрерывной справа функцией;

ü .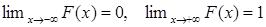

Функция распределения содержит всю вероятностную информацию о случайной величине Х. В частности, P(XÎ(a,b])=F(b)-F(a) для любых чисел a£ b. Дискретную случайную величину удобно представлять в виде таблицы

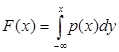, p_k=P(X=x_k) (1). Случайная величина Х называется непрерывной, если её функция распределения дифференцируема, т.е. существует производная p(x)=F’(x), называемая плотностью распределения случайной величины Х, или сокращенно плотностью вероятности. В частности, . Плотность распределения обладает следующими свойствами:

ü р(х)³0 при любом xÎR;

ü .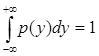

Математическое ожидание (среднее значение) дискретной случайной величины Х, имеющей распределение (1), есть по определению сумма ряда 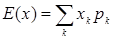при условии его абсолютной сходимости. Для непрерывной случайной величины Х с плотностью распределения р(х) математическое ожидание – это интеграл 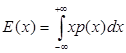также при условии, что он абсолютно сходится. Математическое ожидание имеет следующие свойства (X,Y– произвольные случайные величины, a, b – константы):

ü E(aX+bY)=aE(X)+bE(Y);

ü Если X³Y при всех реализациях, то E(X) ³ E(Y);

ü Если X – непрерывная случайная величина с плотностью распределения p(x), а g(x), xÎR – числовая функция, то для случайной величины Y= g(X ) справедливо равенство ;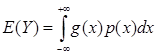

ü E(a)= a.

Другой важнейшей числовой характеристикой случайной величины Х является дисперсия, отражающая степень «разброса» случайной величины относительно среднего значения. Она определяется равенством 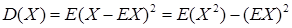. Дисперсия имеет следующие свойства (X,Y– независимые случайные величины, a, b – константы):

ü D(aX+bY)=a² D(X)+b² D(Y);

ü D(a)= 0.

Величину 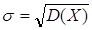называют стандартным отклонением случайной величины Х.

Рассмотрим некоторые конкретные случайные величины, часто используемые в теории вероятностей, математической статистике и их приложениях.

1. Биноминальное распределение. Дискретная случайная величина x_n(p), принимающая значения k=0,1,2,…,n с вероятностями

называется биноминальной случайной величиной с параметрами n и p. Случайная величина с таким распределением возникает в схеме Бернулли. Если случайные величины e_i , i=1, …, n, независимы и принимают значение 1 с вероятностью p и 0 с вероятностью 1-p , то 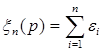, Ex_n(p)= np,

D(x_n(p))= np(1- p).

2. Пуассоновское распределение. Дискретная величина P(l), принимающая значения k=0, 1,…, с вероятностями 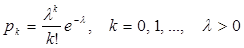, называется пуассоновской случайной величиной с параметром l. Пуассоновское распределение широко используется в теории массового обслуживания. Число l носит название интенсивность. Е(P(l))=D(P(l))=l.

3. Равномерное распределение. Непрерывная случайная величина Х, плотность распределения которой задается формулой , называется равномерной на отрезке [a,b]. .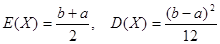

4. Показательное (экспоненциальное) распределение. Непрерывная величина Х, плотность распределения которой задается формулой 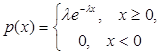, называется показательной или экспоненциальной с параметром l. Это распределение находит широкое применение в демографических исследованиях. .

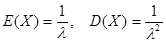5. Нормальное (гауссовское) распределение. Непрерывная случайная величина Х, плотность распределения которой задается формулой 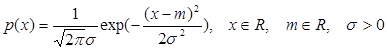, называется нормальной или гауссовской с параметрами m и s². Часто используется обозначение XÎN(m, s²). Нормальная случайная величина с m=0 и s²=1 называется стандартной нормальной величиной. Е(Х)=m, D(X)= s².

Существуют и другие виды распределений. Более подробно о них можно узнать в учебниках [2], [7].