Понятие об идее коррекции ошибок
Для того чтобы в принятом сообщении можно было обнаружить ошибку, это сообщение должно обладать некоторой избыточной информацией, позволяющей отличить ошибочный код от правильного. Например, если переданное сообщение состоит из трех абсолютно одинаковых частей, то в принятом сообщении отделение правильных символов от ошибочных может быть осуществлено по результатам накопления посылок одного вида, например 0 или 1. Для двоичных кодов этот метод можно проиллюстрировать следующим примером:
10110 – переданная кодовая комбинация;
10010 – 1-я принятая комбинация;
10100 – 2-я принятая комбинация;
00110 – 3-я принятая комбинация;
10110–накопленная комбинация.
Как видим, несмотря на то, что во всех трех принятых комбинациях были ошибки, накопленная не содержит ошибок[1].
Принятое сообщение может также состоять из кода и его инверсии. Код и инверсия посылаются в канал связи как одно целое. Ошибка на приемном конце выделяется при сопоставлении кода и его инверсии (подробнее см. тему 7).
Для того чтобы искажение любого из символов сообщения привело к запрещенной комбинации, необходимо в коде выделить комбинации, отличающиеся друг от друга в ряде символов, часть из этих комбинаций запретить и тем самым ввести в код избыточность. Например, в равномерном блочном коде считать разрешенными кодовые комбинации с постоянным соотношением нулей и единиц в каждой кодовой комбинации. Такие коды получили название кодов с постоянным весом. Для двоичных кодов число кодовых комбинаций в кодах с постоянным весом длиной в п символов равно
, (55)
где l – число единиц в кодовом слове. Если бы не существовало условия постоянного веса, то число комбинаций кода могло бы быть гораздо большим, а именно 2n. Примером кода с постоянным весом может служить стандартный телеграфный код №3 (см, приложение 4). Комбинации этого кода построены таким образом, что на 7 тактов, в течение которых должна быть принята одна кодовая комбинация, всегда приходятся три токовые и четыре безтоковые посылки. Увеличение или уменьшение количества токовых посылок говорит о наличии ошибки.
Еще одним примером введения избыточности в код является метод, суть которого состоит в том, что к исходным кодам добавляются нули либо единицы таким образом, чтобы сумма их всегда была четной или нечетной. Сбой любого одного символа всегда нарушит условие четности (нечеткости), и ошибка будет обнаружена. В этом случае комбинации друг от друга должны отличаться минимум в двух символах (см. задачу 6.9), т. е. ровно половина комбинаций кода является запрещенной (запрещенными являются все нечетные комбинации при проверке на четкость или наоборот).
Во всех упомянутых выше случаях сообщения обладают избыточной информацией. Избыточность сообщения говорит о том, что оно могло бы содержать большее количество информации, если бы не многократное повторение одного и того жекода, не добавление к коду его инверсии, не несущей никакой информации, если бы не искусственное запрещение части комбинаций кода и т. д. Но все перечисленные виды избыточности приходится вводить для того, чтобы можно было отличить ошибочную комбинацию от правильной.
Коды без избыточности обнаруживать, а тем более исправлять ошибки не могут[2]. Минимальное количество символов, в которых любые две комбинации кода отличаются друг от друга, называется кодовым расстоянием. Минимальное количество символов, в которых все комбинации кода отличаются друг от друга, называется минимальным кодовым расстоянием. Минимальное кодовое расстояние – параметр, определяющий помехоустойчивость кода и заложенную в коде избыточность. Минимальным кодовым расстоянием определяются корректирующие свойства кодов.
В общем случае для обнаружения r ошибок минимальное кодовое расстояние
(56)
Минимальное кодовое расстояние, необходимое для одновременного обнаружения и исправления ошибок,
(57)
где s – число исправляемых ошибок.
Для кодов, только исправляющих ошибки,
(58)
Для того чтобы определить кодовое расстояние между двумя комбинациями двоичного кода, достаточно просуммировать эти комбинации по модулю 2 и подсчитать число единиц в полученной комбинации (см. задачу 6.21).
Понятие кодового расстояния хорошо усваивается на примере построения геометрических моделей кодов. На геометрических моделях в вершинах n-угольников, где n – значность кода, расположены кодовые комбинации, а количество ребер n-угольника, отделяющих одну комбинацию от другой, равно кодовому расстоянию (см. задачу 6.19).
Если кодовая комбинация двоичного кода А отстоит от кодовой комбинации В на расстоянии d, то это значит, что в коде А нужно d символов заменить на обратные, чтобы получить код В, но это не означает, что нужно d добавочных символов, чтобы код обладал данными корректирующими свойствами. В двоичных кодах для обнаружения одиночной ошибки достаточно иметь 1 дополнительный символ независимо от числа информационных разрядов кода, а минимальное кодовое расстояние d0= 2.
Для обнаружения и исправления одиночной ошибки соотношение между числом информационных разрядов nи и числом корректирующих разрядов nк, должно удовлетворять следующим условиям:
, (59)
, (60)
при этом подразумевается, что общая длина кодовой комбинации
. (61)
Для практических расчетов при определении числа контрольных разрядов кодов с минимальным кодовым расстоянием d0 = 3 удобно пользоваться выражениями:
, (62)
если известна длина полной кодовой комбинации n, и
, (63)
если при расчетах удобнее исходить из заданного числа информационных символов nи[3].
Для кодов, обнаруживающих все трехкратные ошибки (d0= 4),
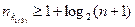, (64)
или
, (65)
Для кодов длиной в n символов, исправляющих одну или две ошибки (d0 = 5),
, (66)
Для практических расчетов можно пользоваться выражением
, (67)
Для кодов, исправляющих 3 ошибки (d0 = 7),
, (68)
Для кодов, исправляющих s ошибок (d0 = 2s+ 1),
. (69)
Выражение слева известно как нижняя граница Хэмминга [16], а выражение справа – как верхняя граница Варшамова – Гильберта [3][4].
Для приближенных расчетов можно пользоваться выражением
. (70)
Можно предположить, что значение nk будет приближаться к верхней или нижней границе в зависимости от того, насколько выражение под знаком логарифма (см. 70) приближается к целой степени двух.
Задача 6.1.Правильность сигнала при использовании метода Бодо – Вердана определяется по результатам накопленных посылок одного вида. Этот метод позволяет исправлять ошибки всегда, если ошибка при повторной передаче не повторяется в одном и том же разряде. Сколько раз надо повторить передаваемое сообщение, чтобы можно было исправлять n-кратные ошибки?
Решение.При 2п повторениях число нулей и единиц в каждом разряде искаженных кодов сравняется. Еще одного повторения будет достаточно для исправления искажения, т. е.
,
где N – число повторений, а n – кратность ошибки.
Задача 6.2.Определить необходимое число повторений сообщения, передаваемого двоичным кодом, для исправления двукратных ошибок. Показать процесс исправления ошибки на конкретном примере.
Задача 6.3.Влияет ли длина передаваемой комбинации на допустимую кратность ошибок, исправляемых методом Бодо – Вердана?
Задача 6.4.Чему равно общее количество комбинаций пятизначного двоичного кода с постоянным весом W = 2? Построить все комбинации такого кода.
Задача 6.5.Требуется построить код для передачи 32 сообщений двоичными комбинациями с постоянным весом W = 3. Какова минимальная длина комбинаций такого кода?
Задача 6.6. Показать процесс обнаружения ошибки кодом с постоянным весом на примере произвольного двоичного кода с числом разрядов не менее четырех.
Задача 6.7. Чему равны исходные комбинации кодов, если система работает с трехкратным повторением исходного сигнала, а принятые комбинации имеют вид: 11110, 00110, 11001, 10101, 11001, 01101, 11101, 11110, 11000?
Задача 6.8. Добавьте к приведенным ниже словам нули и единицы таким образом, чтобы в результате проверок на четность мог быть обнаружен любой единичный сбой: 111011, 111010, 111000, 111100, 110111, 111101, 011001, 110000.
Задача 6.9. Пользуясь приложением 3, построить из стандартного телеграфного кода №2 два кода, обнаруживающих одиночные ошибки.