Развертка поверхности неправильной полной пирамиды

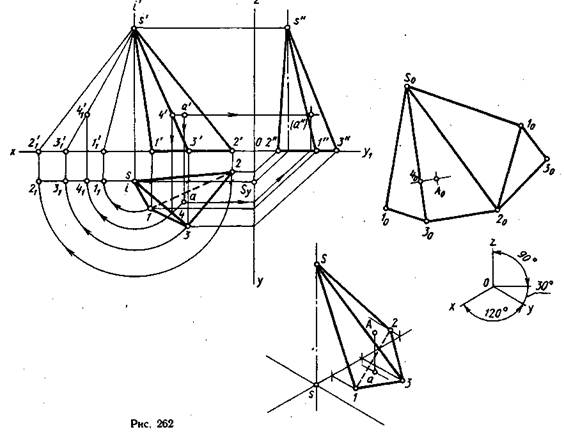
Развертка поверхности неправильной пира­миды будет состоять из неправильных треуголь­ников боковой поверхности и неправильного треугольника, лежащего в основании, совме­щенных в одну плоскость, причем их взаимное расположение на развертке должно соответ­ствовать взаимному расположению на ортого­нальных проекциях. Так как у неправильной пирамиды стороны основания разные и ребра боковой поверхности не равны между собой, сначала находят натуральную величину всех боковых ребер (рис. 262). Для этого исполь­зуют один из методов определения натураль­ной величины отрезка прямой общего поло­жения. В данном случае использован метод вращения. Боковые ребра вращают вокруг оси, проведенной через вершину пирамиды S перпендикулярно плоскости Н. На чертеже фронтальная проекция оси вращения t' прове­дена через фронтальную проекцию вершины s' перпендикулярно оси Ох. Горизонтальные про­екции ребер s₁, s₂ и s₃ поворачивают до положения, параллельного оси Ох. При этом горизонтальные проекции точек 1, 2 и 3 займут положение 1₁, 2₁ и 3₁. От этих точек проводят линии проекционной связи на фронтальную плоскость проекций для получения их фронталь­ных проекций 1׳₁, 2׳₁ и 3׳₁. Затем фронтальные проекции точек соединяют с фронтальной проек­цией s' вершины S прямыми линиями, которые и будут натуральной величиной ребер (1׳₁s׳, 2׳₁s׳ и 3׳₁s׳).

Стороны основания 1 2, 2 3 и 1 3 спроецировались в натуральную величину на горизонталь­ную плоскость проекций. Зная натуральные величины всех элементов пирамиды, присту­пают к построению развертки ее поверхно­сти. При построении развертки боковой поверх­ности используют способ построения треуголь­ников по трем заданным сторонам. Построение можно начать с любой грани боковой поверх­ности, например с грани 1S3 (рис. 262). Сна­чала на свободном месте чертежа проводят произвольную прямую и на ней откладывают натуральную величину стороны основания 1₀3₀, взятую с горизонтальной проекции. Затем из точки 1₀ радиусом, равным натуральной вели­чине ребра SI (s'1'₁), а из точки 3₀ радиусом, равным натуральной величине ребра S3 (s'3׳₁), делают засечки до пересечения в точке S₀, которая будет вершиной развертки боковой поверхности пирамиды. Далее строят боковую

грань 3S2. Для этого на фронтальной про­екции циркулем измеряют натуральную величи­ну ребра S2 (s'2'₁) и на развертке этим радиу­сом из вершины S₀, а из точки З₀ радиусом 3 2, взятым с горизонтальной проекции, делают засечки до пересечения в точке 2₀. Соединив точку 2₀ прямой с вершиной S₀, получим вторую грань 3₀S₀2₀ боковой поверхности пирамиды. Третья грань и основание строятся тем же способом.

Построение полной неправильной пирамиды в аксонометрии

На рис. 262 пирамида построена в прямо­угольной изометрической проекции. Построение следует начинать с ее основания. Поскольку в основании лежит неправильный треугольник, стороны которого не параллельны ни одной из осей координат, то сначала определяют координаты вершин основания (1, 2, 3) отно­сительно горизонтальной проекции s верши­ны S. Для этого на линию проекционной связи, идущую через горизонтальную проекцию s па­раллельно оси Ох, проводят прямую из вер­шины 2 параллельно оси Оу (рис. 262). Через вершины 1 и 3 проводить прямые не надо, так как здесь имеются линии проекционной связи, идущие от этих точек параллельно оси Оу. Таким образом, координаты горизонтальных проекций вершин получились заданными гра­фически.

На свободном месте чертежа проводят две прямые, параллельные аксонометрическим осям Ох и Оу прямоугольной изометрической про­екции, и в точке их пересечения задают вто­ричную горизонтальную проекцию s верши­ны S. Сама вершина находится на прямой, параллельной оси Oz, на которой откладывают высоту пирамиды, взятую с фронтальной или профильной проекции. Далее строят основание пирамиды. Прямую, проведенную на ортого­нальном чертеже в плоскости Н через горизон­тальную проекцию s вершины S параллельно оси Ох, принимают за базовую линию. Рас­стояния, измеренные по этой линии от точки s до точек пересечения с линиями проекционной связи, идущими параллельно оси Оу через точки 1, 2 и 3, переносят в аксонометрию. Там их откладывают от вторичной горизонтальной проекции вершины s на линии, проходящей параллельно аксонометрической оси Ох. Из полученных точек проводят прямые, парал­лельные аксонометрической оси Оу, и на них откладывают расстояния до точек 1, 2 и 3, взятые с горизонтальной проекции. Построен­ные вершины основания соединяют между собой и с вершиной S прямыми. Основание пира­миды и боковая грань 1S2 в изометрии будут невидимыми.

Построение точки, лежащей на боковой поверхности пирамиды

Построение ортогональных проекций точки, лежащей на боковой поверхности неправиль­ной пирамиды, может быть выполнено так же, как и на правильной пирамиде.

На рис. 262 точка А лежит на боковой грани пирамиды 3S2 и задана ее фронтальной проекцией а'. Требуется построить профильную и горизонтальную проекции этой точки, постро­ить ее в изометрии и на развертке.

При построении проекции точки А в ортого­нальных проекциях нужно помнить о том, что все боковые грани, и в том числе грань 3S2, на которой лежит точка А, проецируются на все плоскости проекций как треугольники. Для по­строения горизонтальной проекции точки в пло­скости грани 3S2 проводят вспомогательную прямую (горизонталь). Ее фронтальную про­екцию проводят через точку а' параллельно основанию до пересечения с фронтальной проекцией ребра s'3' в точке 4'. Затем эту вспомогательную прямую строят на горизон­тальной проекции, для чего сначала находят горизонтальную проекцию точки А, а потом через эту точку параллельно горизонтальной проекции стороны основания 3 2 проводят горизонтальную проекцию вспомогательной прямой, на которую опускают линию про­екционной связи от фронтальной проекции а' точки А. Профильную проекцию а" точки А можно построить, используя для этого только линии проекционной связи.

Чтобы построить точку А на развертке, необходимо сначала построить точку 4₀ на ребре S₀3₀ развертки боковой поверхности (рис. 262). Для этого строят точку 4₁ на отрезке s'3׳₁, который является натуральной величиной ребра 3S. Затем измеряют рассто­яние от s' до точки 4₁ и переносят его на соот­ветствующее ребро развертки, где через точ­ку 4₀ параллельно стороне 3₀2₀ проводят вспомогательную прямую, на которой от точки 4₀ откладывают расстояние до точки А₀,. взятое с горизонтальной проекции, так как на плоскость Н отрезок 4а проециру­ется в натуральную величину.

Построение точки А в изометрической про­екции начинают с построения ее вторичной проекции (рис. 262). Затем от вторичной горизонтальной проекции а точки А параллельно оси Оz проводят прямую, на которой отклады­вают расстояние от основания пирамиды до точки А, взятое с фронтальной или профильной проекции.