Пересечение прямой с поверхностью Конуса.

Способ решения этой задачи зависит от поло­жения прямой относительно боковой поверх­ности конуса и плоскости Н.

На рис. 297 изображены прямой круговой конус и прямая АВ общего положения, пере секающая боковую поверхность конуса. Тре­буется построить точки входа и выхода этой прямой. Боковая поверхность конуса не яв­ляется проецирующей, поэтому для определе­ния точек входа и выхода используют вспомо­гательную секущую плоскость.

Если через прямую АВ провести фронталь­но-проецирующую плоскость, то в пересечении будет эллипс, для построения которого потре­буются дополнительные построения, а это ус­ложняет решение задачи.

Если через прямую АВ провести горизон­тально-проецирующую плоскость, то в пересече­нии получится гипербола, построение которой также усложняет построения.

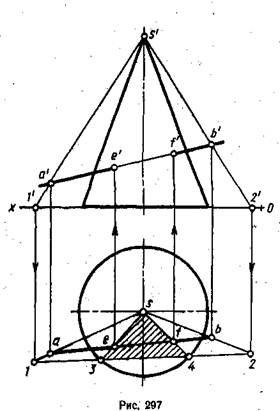Простыми линиями пересечения боковой по­верхности конуса с плоскостью являются ок­ружность и треугольник. В данном случае ок­ружность использовать нельзя. Известно, что треугольник в пересечении получается тогда, когда плоскость, пересекая конус, проходит че­рез его вершину. Поэтому через прямую SB следует провести такую плоскость, которая пройдет через вершину конуса, Эту плоскость задают треугольником общего положения ASB.

Затем строят фронтальную и горизонталь­ную проекции данной плоскости, строят ли­нию пересечения этой плоскости с поверх­ностью конуса, определяют точки, в которых линия пересечения поверхности конуса с вспо­могательной плоскостью пересекается с пря­мой АВ. Таков план решения задачи. Для его осуществления в плоскости V через точку s' и любые две точки, например точки V и b', принадлежащие фронтальной проекции задан­ной прямой, проводят до оси Оx фронтальные проекции двух прямых s'1' и s'2', определяю­щих фронтальную проекцию вспомогательной плоскости, заданной треугольником. Сторона 1'2' плоскости треугольника сливается с осью Ох и частично с проекцией основания конуса. Точки 1' и 2' являются фронтальными проек­циями точек пересечения сторон треугольника 1S2 сплоскостью H.

Строят горизонтальную проекцию вспомога­тельной плоскости. Горизонтальные проекции боковых сторон треугольника пройдут через точки s, а и b и закончатся в точках 1 и 2, ко­торые будут лежать в пересечении с линиями проекционной связи, проведенными от точек 1' и 2'. Соединив прямой линией точки 1 и 2

на горизонтальной проекции, получают линию пересечения вспомогательной плоскости с плоскостью Н и плоскостью основания конуса, лежащей в плоскости Н. Отрезок 34 будет от­резком, по которому вспомогательная плос­кость, заданная треугольником, пересеклась с основанием конуса. Соединив точки 34 с точ­кой s (горизонтальная проекция вершины ко­нуса), получают горизонтальную проекцию треугольника, по которому эта плоскость пе­ресекла поверхность конуса. Там, где горизон­тальные проекции сторон треугольника пере­секаются с горизонтальной проекцией ab пря­мой АВ, получаются точки е и f — горизон­тальные проекции искомых точек. Точки е' и f' строят с помощью. линий проекционной связи, проведенных от точек е и f с горизон­тальной проекции.

На рис, 298 изображен прямой круговой ко­нус, боковую поверхность которого пересекает горизонтальная прямая АВ. Требуется постро­ить точки, в которых прямая АВ пересекает боковую поверхность конуса. Задачу решают с помощью вспомогательной горизонтальной плоскости Р, проведенной через прямую АВ.

Плоскость Р пересекает поверхность конуса по окружности (Параллели), диаметр которой равен отрезку следа плоскости Р_ѵ, заключенному в очерк конуса. На горизонтальной проек­ции проводят эту окружность (горизонтальную проекцию параллели), находят точки е и f, в которых она пересекается с горизонтальной проекцией ab прямой АВ. Их фронтальные проекции определяют с помощью линий проек­ционной связи, проведенных от точек е и f с горизонтальной проекции до. пересечения с фронтальной проекцией а'b' прямой АВ. На фронтальной плоскости проекций точка F будет невидимой, так как точка F расположе­на в той части конуса, которая на этой про­екции не видна.

На рис. 299 изображен прямой круговой ко­нус, поверхность которого пересекают две проецирующие прямые АВ и CD. Требуется определить точки их входа и выхода. Эта за­дача решается двумя способами.

Первый способ. Прямая АВ на горизонталь­ной проекции спроецировалась в точку. В ту же точку проецируются и точки входа и выхода этой прямой. Следовательно, имеются гори­зонтальные проекции этих точек и необходимо только определить их фронтальное проекции. Для этого через горизонтальную проекцию вершины s и точку, являющуюся горизон­тальной проекцией прямой АВ и лежащих на ней точек входа и выхода, проводят образую­щую. Затем строят фронтальную проекцию этой образующей. Там, где она пересечет фронтальную проекцию а' b' заданной прямой

АВ, и будет лежать фронтальная проекция искомой точки е', точки входа прямой АВ. Фронтальная проекция f точки F выхода этой прямой лежит в том месте, где прямая а'b' пересеклась с отрезком, в который спроецировалось основание конуса. Точка F изобразилась здесь невидимой, так как лежит не на контурной окружности основания, а внутри круга основа­ния. На горизонтальной проекции точка F тоже будет невидимой.

Второй способ.Точки входа и выхода пря­мой CD на рис. 299 строят с помощью па­раллели, проведенной на горизонтальной про­екции через горизонтальную проекцию cd пря­мой CD. Затем строят фронтальную проекцию параллели. В пересечении ее с фронтальной проекцией c'd' прямой CD находится точка ш' — фронтальная проекция точки входа пря­мой CD. Точка т' будет невидимой, так как точка М лежит в той части конуса, которая на фронтальной проекции не видна. Точка N (точка выхода прямой CD) находится в пере­сечении этой прямой с плоскостью основания. Ее горизонтальная проекция совпадает с го­ризонтальной проекцией прямой, а фронталь­ная проекция п' находится в пересечении проекции c'd' с отрезком, в который спроецировалось основание конуса.

Пересечение прямой с поверхностью шараможет быть построено несколькими способами. Выбор способа зависит от положения прямой относительно плоскостей проекций. На рис. 300 изображены две проекции шара и прямой АВ общего положения. Требуется построить точ­ки пересечения этой прямой с поверхностью шара. При решении подобных задач следует помнить о том, что шар — это единственное геометрическое тело, поверхность которого пересекается плоскостью любого положения по окружности. При решении данной задачи необ­ходимо через прямую АВ общего положения провести проецирующую плоскость. На рис. 300 это горизонтально-проецирующая плоскость. Шар будет пересекаться плоскостью Р по ок­ружности, которая на горизонтальной проек­ции проецируется в отрезок 12, совпадающий с горизонтальной проекцией прямой и горизон­тальным следом Р_н плоскости Р. На фрон­тальной проекции эта окружность изобразится эллипсом, для построения которого требуются дополнительные построения. Это усложняет задачу. Проще и точнее найти точки пересе­чения окружности с прямой. Поэтому для ре­шения задачи удобнее всего применить спо­соб перемены плоскостей проекций. На рис. 300 плоскость V 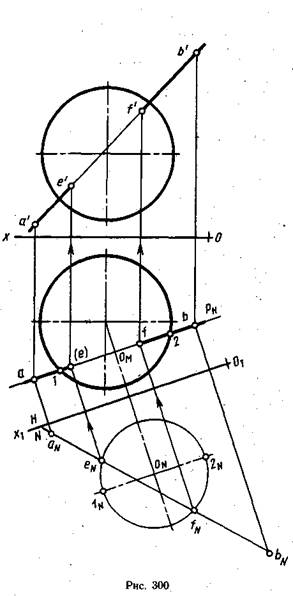заменена на плоскость N. Кон­турная образующая шара на плоскости N не изображена, так как для построения искомых точек она не нужна. Изображены только окружность пересечения и новая проекция a_Nb_N прямой АВ. На плоскости N построена проекция центра шара o_N на такой же высоте, на ко­торой его фронтальная проекция находится над осью Ох на плоскости V. Из точки o_N опи­сана окружность радиусом о1, взятым с гори­зонтальной проекции. Эта окружность пере­секается с проекцией a_Nb_N прямой в точках e_N и f_N, которые будут проекциями искомых точек. Положение горизонтальных и фронталь­ных проекций точек входа и выхода прямой АВ определяют с помощью линий проекцион­ной связи, проведенных от точек e_N и f_N снача­ла на плоскость H, а затем на плоскость V. На горизонтальной плоскости проекций точка Е будет невидимой, так как располагается в той части шара, которая не видна на горизонталь­ной проекции.

На рис. 301 изображен шар в двух ортого­нальных проекциях, который пересекается го­ризонтальной прямой АВ. Требуется построить точки пересечения прямой АВ с поверхностью шара.

Решение задачи упрощается частным поло­жением прямой.. Здесь через прямую АВ про­водят фронтально-проецирующую плоскость. Эта плоскость Р пересечет шар по окружности, которая на фронтальной плоскости проекций изобразится отрезком, совпадающим с фрон­тальным следом Р_ѵ плоскости Р и фронталь­ной проекцией а'b' прямой АВ. На горизон­тальной проекции линия пересечения изобразит­ся окружностью, радиус которой берется на фронтальной проекции от оси шара до кон­турной образующей шара по следу Р_ѵ. Точки е и f, в которых проекция окружности пересече­ния пересекается с горизонтальной проекцией ab прямой АВ, будут горизонтальными проек­циями искомых точек. Фронтальные проекции' е' и f' строят с помощью линий проекционной связи, проведенных от горизонтальных проек­ций точек е и f. На фронтальной проекции точка, Е будет невидимой, так как расположе­на на той части шара, которая не видна.

На рис. 302 в двух ортогональных проекциях изображен шар, поверхность которого пересе­кается двумя проецирующим прямыми, пер­пендикулярными плоскости Н. Требуется по­строить точки пересечения этих прямых с по­верхностью шара. Задача решается двумя способами.

Первый способ. Точки входа и выхода пря­мой АВ строят с помощью горизонтально-проецирующей плоскости Р так же, как на рис. 301, только там прямая заключена во фронтально-проецирующую плоскость.

Второй способ. Построение точек пересечения прямой (прямая CD) с поверхностью шара выполняется с помощью параллелей. Горизон­тальные проекции этих параллелей проводят через точку, в которую проецируются прямая CD и лежащие на ней точки входа и выхода. Проекции этих параллелей здесь совпадают и изображаются окружностью. На рис. 302 про­ведена дуга этой окружности. С помощью линии проекционной связи строят фронтальные проекции параллелей, которые представляют собой прямые, расположенные параллельно оси Ох на одинаковом расстоянии от экватора (на рис. 302 они проведены частично). Точки пересечения фронтальных проекций параллелей с проекцией c'd' прямой CD будут фронталь­ными проекциями к' и п' точек К и N.

 

 

§35. ПОСТРОЕНИЕ ЛИНИИ ВЗАИМНОГО