Пересечение прямой с поверхностью призмы.

Путь решения этой задачи зависит от расположения прямой и боковых граней призмы от­носительно плоскости основания, к которому они могут располагаться наклонно (рис. 291) или перпендикулярно (рис. 292).

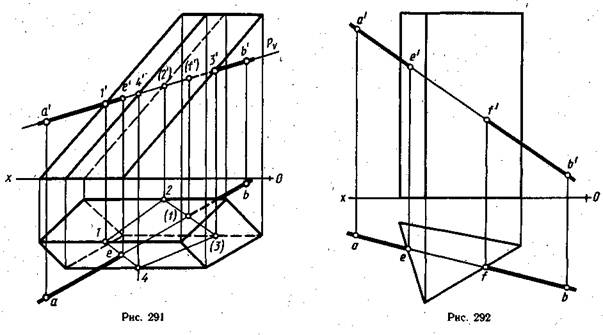
На рис. 291 изображена наклонная четы­рехугольная призма, боковую поверхность ко­торой пересекает прямая линия общего поло­жения АВ. Требуется построить точки пересе­чения прямой АВ с боковой поверхностью призмы, которые называются точкой вхо­да и точкой выхода.

Боковая поверхность призмы в этом случае не является проецирующей, и для того, чтобы найти точки пересечения, через прямую АВ проводят проецирующую плоскость. На рис. 291 это фронтально-проецирующая плоскость Р. Фронтальный след Р_ѵ этой плоскости проводят через фронтальную проекцию прямой а'b'. Плоскость Р пересечет призму по четырех­угольнику.

На горизонтальной плоскости проекций строят проекцию этого четырехугольника (1, 2, 3, 4). Для этого от фронтальных проекций точек, в которых ребра призмы пересеклись с плоскостью Р, проводят линии проекционной связи до соответствующих горизонтальных проекций ребер. Полученные точки соединяют тонкой линией и определяют, в каких точках эта линия, пересеклась с горизонтальной про­екцией прямой ab. Этими точками являются точки е и f. Фронтальные проекции е' и f׳ то­чек пересечения прямой с боковой поверхнос­тью призмы строят с помощью линий проек­ционной связи, проведенных от точек е и f с горизонтальной проекции. На горизонтальной и фронтальной плоскостях проекций точка Е бу­дет видимой, так как лежит на грани, види­мой на этих проекциях. Точка F находится на грани невидимой на горизонтальной и фрон­тальной проекциях, поэтому она изобразится невидимой. Обозначения проекций невиди­мых точек взяты в скобки. Условимся учас­ток прямой линии, расположенный между точкой входа и точкой выхода прямой, про­ходящей внутри геометрического тела, изобра­жать тонкой сплошной линией.

 

 

На рис. 292 в двух ортогональных проек­циях изображена прямая треугольная призма, боковую поверхность которой пересекает пря­мая линия АВ общего положения. Требует­ся построить точки входа и выхода этой пря­мой.

Поскольку боковая поверхность призмы перпендикулярна ее основаниям, то она бу­дет проецирующей. В этом случае для опре­деления точек пересечения вспомогательную плоскость через заданную прямую не проводят, так как на горизонтальную плоскость проекций, где боковая поверхность призмы проецируется в ломаную линию, отрезки которой совпада­ют со сторонами треугольника основания призмы. Этот треугольник пересекается с пря­мой ab в точках e и f. Эти точки и будут горизон­тальными проекциями искомых точек. Фрон­тальные проекции е' и f׳ точек Е и F строят с помощью линий проекционной связи. Так оп­ределяют точки входа и выхода, если боковая поверхность призмы проецирующая, незави­симо от положения прямой АВ.

Пересечение прямой с поверхностью пира­миды.Рассмотрим три случая пересечения прямой с поверхностью пирамиды.

На рис. 293 изображена треугольная пира­мида, которую пересекает прямая АВ общего положения. Требуется построить точки входа и выхода.

Грани боковой поверхности пирамиды не являются проецирующими, поэтому для по­строения точек входа и выхода прямой через прямую АВ проводят проецирующую плос­кость. На рис. 293 проведена фронтально-проецирующая плоскость Р. Фронтальный след Р_ѵ плоскости Р проводят через фронтальную проекцию а'b' прямой АВ. Плоскость Р пере­сечет боковую поверхность пирамиды по тре­угольнику, который на фронтальную плос­кость проекций проецируется в отрезок, сов­падающий с фронтальной проекцией а'b' пря­мой АВ и фронтальным следом Р_ѵ.

Для построения горизонтальной проекции этого треугольника с помощью линий проек­ционной связи, проведенных с фронтальной плоскости проекций из точек 1' и 3' на горизонтальную, находят точки 1 а 3. Построить точку 2 только с помощью линии проекцион­ной связи на горизонтальной проекции нель­зя, так как она сливается с горизонтальной проекцией ребра. Необходимо сделать дополнительное построение, т. е. через точку 2 в плоскости грани KSN проводят горизонталь. Ее фронтальная проекция пройдет через точку 2' параллельно оси Ох, а горизонтальная проекция — параллельно горизонтальной проекции kn стороны KN основания треуголь­ника. От точки, в которой фронтальная про­екция горизонтали пересекла проекцию ребра s'n', проводят линию проекционной связи до пересечения ее с горизонтальной проекцией ребра sn. От этой точки параллельно kn про­водят горизонтальную проекцию горизонтали до пересечения ее с горизонтальной проекци­ей ребра sk в точке 2. Эта точка и будет точкой, которую нужно соединить с точками 1 и 3 прямыми линиями. Получился треуголь­ник, по которому плоскость Р пересекла пи­рамиду. Далее определяют точки пересечения горизонтальных проекций сторон треугольника 1 2 3 сгоризонтальной проекцией ab прямой АВ. Этими точками будут точки е и f. С по­мощью линий проекционной связи, проведен­ных с горизонтальной проекции от точек e и f на фронтальную проекцию, строят фронталь­ные проекции е' и f' точек Е и F. На фронталь­ной плоскости проекций точка F' будет невидимой, так как лежит на грани MSN, неви­димой на плоскости проекций V.

На рис. 294 изображена четырехугольная пирамида, боковую поверхность которой пере­секает горизонтальная прямая АВ. Требуется построить точки пересечения прямой с боковой поверхностью пирамиды.

Поскольку боковая- поверхность пирамиды не является проецирующей, то определять точки входа и выхода прямой в этом случае можно только используя дополнительную про­ецирующую плоскость, проведенную через пря­мую. В данном случае лучше провести плос­кость, параллельную плоскости Н. Поэтому через прямую АВ проводят фронтально-про­ецирующую плоскость Р. Эта плоскость будет параллельной основанию пирамиды и пересе­чет ее боковую поверхность по четырехуголь­нику, стороны которого будут параллельны сторонам основания.

С помощью линий проекционной связи стро­ят четырехугольник 1 2 3 4, для этого с фрон­тальной проекции, где линия пересечения пи­рамиды с плоскостью Р проецируется в пря­мую, совпадающую со следом Р_ѵ и фронталь­ной проекцией а`b' прямой АВ, от точки 1' про­водят линию проекционной связи до пересече­ния ее с горизонтальной проекцией соответ­ствующего ребра в точке 1. Через точку 1 па­раллельно сторонам основания проводят го­ризонтальные проекции сторон четырехуголь­ника, лежащего в плоскости Р. Далее определяют точки, в которых горизонтальная проекция линии пересечения (четырехугольник 1 2 3 4) пересекается с горизонтальной проек­цией ab прямой АВ. Этими точками будут точки е и f. С помощью линий проекционной связи находят их фронтальные проекции е' и f'. На фронтальной плоскости проекций точка F будет невидимой, так как она располагается на невидимой грани, и часть прямой АВ тоже будет невидимой.

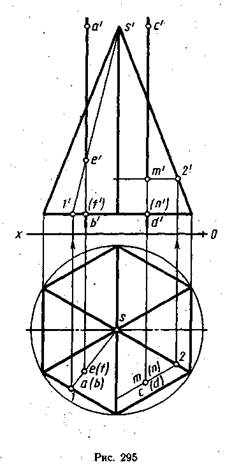
На рис. 295 изображена шестиугольная пирамида, поверхность которой пересекают две проецирующие прямые АВ и CD. Требует­ся построить точки входа и выхода этих пря­мых. Так как прямые являются проецирую­щими, то в данном случае горизонтальные проекции точек входа и выхода прямых АВ и CD и сами прямые проецируются в одну точку каждая. Поставленная задача на рис. 295 решается двумя способами.

Рассмотрим первый способ. Прямая АВ в точке F пересекает основание пирамиды. Фрон­тальная проекция этой точки f' находится в пересечении фронтальных проекций а'b' пря­мой АВ и. основания пирамиды. Точка f' будет невидимой. Горизонтальная проекция точки F совпадает с горизонтальной проекцией пря­мой АВ. Для построения фронтальной проек­ции е' точки Е через ее горизонтальную про­екцию и горизонтальную проекцию вершины s проводят вспомогательную прямую в плос­кости боковой грани. Затем находят фронталь­ную проекцию вспомогательной прямой. В пе­ресечении ее с фронтальной проекцией задан­ной прямой АВ и будет находиться фронталь­ная проекция е' точки Е, в которой прямая АВ пересекает боковую поверхность пирами­ды.

Определение точки входа М прямой CD вы­полняют вторым способом. Через горизонталь­ную проекцию прямой CD, которая здесь проецируется в точку, проводят горизонталь­ную проекцию горизонтали передней правой грани пирамиды. Она пойдет параллельно горизонтальной проекции стороны основания боковой грани. Далее строят фронтальную проекцию горизонтали. Она пойдет парал­лельно оси Ох от точки 2', построенной с по­мощью линии проекционной связи, проведен­ной от горизонтальной проекции точки 2, ле­жащей на соответствующей проекции ребра' боковой поверхности.

В пересечений фронтальной проекции го­ризонтали с фронтальной проекцией c'd' пря­мой CD будет находиться фронтальная проек­ция т' точки М. Фронтальная проекция п' точ­ки N лежит в пересечении проекции c'd' пря­мой CD с прямой, в которую проецируется основание пирамиды. Эта точка будет невиди­мой.

Пересечение прямойс поверхностью прямо­го кругового цилиндра.Возможны несколько случаев расположения прямой относительно боковой поверхности цилиндра, но во всех случаях точки входа и выхода прямой опре­деляются одинаково. Боковая поверхность такого цилиндра является проецирующей. В данном случае. боковая поверхность на горизонтальной проекции спроецируется в окружность; совпадающую с проекцией кон­турной линии оснований, и проекция точки входа и выхода прямой АВ будет находиться на этой окружности в том месте, где горизон­тальная проекция ab прямой АВ пересекает ее (рис. 296). Этими точками будут точки е и f. Фронтальные проекции точек Е и F строят с помощью линий проекционной связи, прове­денных с горизонтальной проекции от точек е и f на фронтальную проекцию а'b' прямой АВ. Фронтальная проекция f' точки F изобра­зится невидимой, так как точка F находится в той части боковой поверхности цилиндра, которая здесь не видна. Часть линии а'b', иду­щая от точки f', тоже будет невидимой.