Ортогональные проекции усеченной призмы
Пересечение призмы проецирующей плоскостью
Форма линии пересечения зависит от формы призмы и от направления секущей плоскости. На рис. 277 показаны примеры пересечения треугольной призмы плоскостями различного положения.
|
Ортогональные проекции усеченной призмы
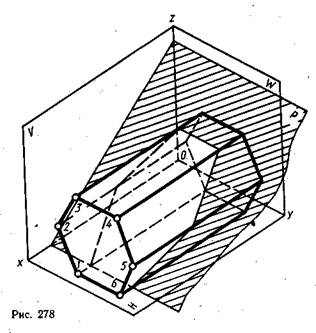
На рис. 278 изображена шестиугольная правильная прямая призма, лежащая одной гранью на плоскости проекций Н. Основания призмы расположены параллельно плоскости проекций W. Призма пересечена фронтально-проецирующей плоскостью Р, которая задана следом Рѵ (рис. 279). Требуется построить ортогональные проекции усеченной призмы, натуральную величину фигуры среза, усеченную призму в изометрии и развертку боковой поверхности усеченной призмы. Будем считать, что плоскость Р отсекла левую часть призмы, которую на проекциях и развертке изобразим тонкими линиями. Оставшуюся (правую) часть называют усеченной призмой и обводят сплошной основной линией.
Так как плоскость Р перпендикулярна плоскости проекции V, то она спроецируется на эту плоскость в прямую линию. На эту же линию спроецируется и фигура среза, лежащая в плоскости Р. Длина отрезка от точек 6'(1') до точек 4' (3') будет натуральной длиной фигуры среза. На профильной плоскости проекций боковые грани призмы проецируются в отрезки, совпадающие со сторонами шестиугольника, лежащего в основании, а ребра боковой поверхности проецируются в точки, совпадающие с вершинами углов основания. Фигура среза на профильной проекции совпадает с проекцией основания и изображается как правильный шестиугольник, так как линии среза принадлежат боковым граням призмы, которые проецируются на профильную плоскость проекций отрезками. Отрезки 3-4, 2-5 и 1-6 проецируются на профильную плоскость проекции без искажения, так как они параллельны оси Оу, т. е. плоскости W. Значит на профильной проекции видна натуральная ширина среза.
На горизонтальную плоскость проекций срез проецируется с искажением, так как плоскость Р, в которой лежит фигура среза, наклонена к плоскости проекций Н. Отрезки 13 и 64 проецируются с искажением. Отрезки 16, 25 и 34 параллельны оси Оу1 на профильной проекции, следовательно, параллельны плоскости Н, поэтому проецируются без искажения. Значит ширина среза и здесь спроецировалась в натуральную величину.
Ни на одной из трех плоскостей проекцій фигура среза не проецируется в натуральную величину, так как плоскость, в которой она лежит, не параллельна ни одной из плоскостей проекций. Для того чтобы построить ее натуральную величину, необходимо расположить фигуру среза параллельно какой-либо плоскости проекции. На рис. 279, а это выполнено способом перемены плоскостей проекций, где плоскость Н заменена на плоскость N, параллельную плоскости Р. Для этого на фронтальной плоскости проекций параллельно фронтальному следу Рѵ плоскости Р на некотором расстоянии от него проведена новая ось О1х1. В этой системе плоскостей проекций плоскость Р, с лежащей в ней фигурой среза, расположена параллельно плоскости N, и новая проекция среза будет иметь натуральную величину.
Из точек 6', 2', 4' перпендикулярно оси О1х1 проводят линии проекционной связи, переносящие на плоскость N расстояния по длине среза. Затем от оси О1х1 откладывают отрезки, взятые с горизонтальной проекции призмы от оси Ох до точек 1...6, точки 1N...6N соединяют отрезками, получают натуральную величину среза.