Понятие о системах массового обслуживания (СМО)

 

Во многих областях экономики, финансов, производства и быта важную роль играют системы массо­вого обслуживания (СМО), т.е. такие системы, в которых, с одной стороны, возникают массовые запросы (требования) на выполнение каких-либо услуг, а с другой стороны, происходит удовлетворение этих запросов.

В качествепримеров СМО в финансово-экономи­ческой сфере можно привести системы, представляющие собой: банки различных типов, страховые организа­ции, налоговые инспекции, ау­диторские службы, различные системы связи (в том числе те­лефонные станции), погрузочно-разгрузочные комплексы (товарные станции), автозаправочные станции, различные предприятия и организации сферы обслуживания (магазины, предприятия массового питания, справочные бюро, парикмахерские, билетные кассы, пункты по обмену валюты, ремонтные мастерские, больницы).

Такие сис­темы как компьютерные сети, системы сбора, хранения и обра­ботки информации, транспортные системы, автоматизирован­ные производственные участки, поточные линии также могут рассматриваться как своеобразные СМО.

В торговле выполняется множество операций в процессе движе­ния товарной массы из сферы производства в сферу потребления. Такими операциями являются: погрузка и выгрузка товаров, пере­возка, упаковка, фасовка, хранение, выкладка, продажа и т. д. Для торговой деятельности характерны массовое поступление товаров, денег, массовое обслу­живание покупателей и т. п., а также выполнение соответствующих операций, которые носят случайный характер. Все это создает не­равномерность в работе торговых организаций и предприятий, порождает недогрузки, простои и перегрузки. Много времени отни­мают очереди, например, у покупателей в магазинах, водителей ав­томашин на товарных базах, ожидающих разгрузки или погрузки. В связи с этим возникают задачи анализа работы, например тор­гового отдела, торгового предприятия или секции, для оценки их деятельности, выявления недостатков, резервов и принятия в конеч­ном итоге мер, направленных на увеличение ее эффективности. Кроме того, возникают задачи, связанные с созданием и внедре­нием более экономичных способов выполнения операций в пределах секции, отдела, торгового предприятия, овощной базы, управления торговли и т. п. Следовательно, в организа­ции торговли методы теории массового обслуживания позволяют определить оптимальное количество торговых точек данного профиля, численность про­давцов, частоту завоза товаров и другие параметры.

Другим ха­рактерным примером систем массового обслуживания могут служить склады или базы снабженческо-сбытовых организа­ций, и задача теории массового обслуживания сводится к тому, чтобы установить оптимальное соотношение между числом по­ступающих на базу требований на обслуживание и числом об­служивающих устройств, при котором суммарные расходы на обслуживание и убытки от простоя транспорта были бы мини­мальными. Теория массового обслуживания может найти при­менение и при расчете площади складских помещений, при этом складская площадь рассматривается как обслуживающее устройство, а прибытие транспортных средств под выгрузку - как требование.

2 Основные характеристики СМО[10]

 

СМО включаетследующие элементы: источник требований, входящий поток требований, очередь, обслуживающее устройство (канал обслуживания), выходящий поток требований (обслуженных заявок).

Каждая СМО предназначена для обслуживания (выполнения) некоторого потока заявок (требований), поступающих на вход системы, в основном, не регулярно, а в случайные моменты времени. Обслуживание заявок также длится не постоянное, заранее известное время, а случайное время, которое зависит от многих случайных причин. После обслуживания заявки канал освобожден и готов к приему следующей заявки. Случайный характер потока заявок и времени их обслуживания приводит к не­равномерной загруженности СМО: в некоторые промежутки времени на входе СМО могут скапливаться необслуженные заявки, что приводит к перегрузке СМО, в некоторые же дру­гие интервалы времени при свободных каналах на входе CMО заявок не будет, что приводит к недогрузке СМО, т.е. к про­стаиванию ее каналов. Заявки, скапливающиеся на входе СМО, либо "становятся" в очередь, либо по какой-то причине невоз­можности дальнейшего пребывания в очереди покидают СМО необслуженными.

Схема СМО изображена на рисунке 5.1.

 

 

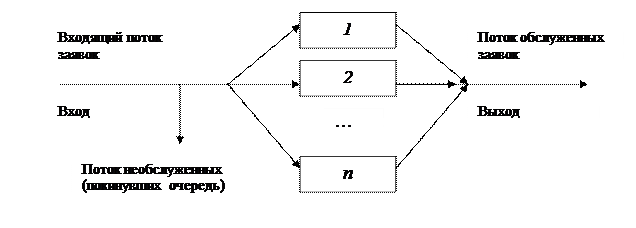
Рисунок 5.1 - Схема системы массового обслуживания

 

Каждая СМО включает в свою структуру некоторое число обслуживающих устройств, которые называют каналами обслуживания. Роль каналов могут играть различные приборы, лица, выполняющие те или иные операции (кассиры, операторы, продавцы), линии связи, автомашины и т.д.

Каждая СМО в зависимости от своих параметров: характера потока заявок, числа каналов обслуживания и их производи­тельности, а также от правил организации работы обладает определенной эффективностью функционирования (пропускной способностью), позволяющей ей более или менее успешно справляться с потоком заявок.

СМО явля­ется предметом изучения теории массового обслуживания.

Цель теории массового обслуживания — выработка рекомен­даций по рациональному построению СМО, рациональной ор­ганизации их работы и регулированию потока заявок для обес­печения высокой эффективности функционирования СМО.

Для достижения этой цели ставятся задачи теории массового обслуживания, состоящие в установлении зависимостей эффек­тивности функционирования СМО от ее организации (пара­метров).

В качестве характеристик эффективности функционирова­ния СМО можно выбрать три основные группы (обычно средних) показателей:

1. Показатели эффективности использования СМО:

1.1. Абсолютная пропускная способность СМО — среднее число заявок, которое сможет обслужить СМО в единицу времени.

1.2. Относительная пропускная способность СМО - от­ношение среднего числа заявок, обслуживаемых СМО в единицу времени, к среднему числу посту­пивших заявок за это же время.

1.3. Средняя продолжительность периода занятости СМО.

1.4. Коэффициент использования СМО — средняя доля времени, в течение которого СМО занята обслужи­ванием заявок.

2. Показатели качества обслуживания заявок:

2.1. Среднее время ожидания заявки в очереди.

2.2. Среднее время пребывания заявки в СМО.

2.3. Вероятность отказа заявке в обслуживании без ожи­дания.

2.4. Вероятность того, что поступившая заявка немедлен­но будет принята к обслуживанию.

2.5. Закон распределения времени ожидания заявки в очереди.

2.6. Закон распределения времени пребывания заявки в СМО.

2.7. Среднее число заявок, находящихся в очереди.

2.8. Среднее число заявок, находящихся в СМО, и т.п.

3. Показатели эффективности функционирования пары "СМО — потребитель", где под "потребителем" понимают всю совокупность заявок или некий их источник (например, средний доход, при­носимый СМО в единицу времени, и т.п.).

Случайный характер потока заявок и длительности их об­служивания порождает в СМО случайный процесс. Поскольку моменты времени T_i и интервалы времени поступле­ния заявок T, продолжительность операций обслуживания Т_обс, про­стоя в очереди T_оч, длина очереди l_оч — случайные величины, то характеристики состояния систем массового обслуживания носят вероятностный характер. Поэтому для решения задач теории массового обслужива­ния необходимо этот случайный процесс изучить, т.е. постро­ить и проанализировать его математическую модель.

Математическое изучение функционирования СМО значи­тельно упрощается, если протекающий в ней случайный про­цесс является марковским. Чтобы случайный процесс был марковским, необходимо и достаточно, чтобы все потоки событий, под воз­действием которых происходят переходы системы из состояния в состояние, были (простейшими) пуассоновскими.

Простейший поток обладает тремя основными свойствами: ординарности, стационарности и отсутствия последействия.

Ординарность потока означает практическую невозмож­ность одновременного поступления 2-х и более требований. На­пример, достаточно малой является вероятность того, что в магазине самообслуживания одно­временно выйдут из строя несколько кассовых аппаратов.

Стационарным называется поток, для которого математиче­ское ожидание числа требований, поступающих в систему в едини­цу времени (обозначим λ), не меняется во времени. Таким образом, вероятность поступления в систему определенного количества тре­бований в течение заданного промежутка времени ∆T зависит от его величины и не зависит от начала его отсчета на оси времени.

Отсутствие последействия означает, что число требова­ний, поступивших в систему до момента T, не определяет того, сколько требований поступит в систему за время (T + ∆T). Например, если в кассовом аппарате в данный момент произо­шел обрыв кассовой ленты и он устранен кассиром, то это не влияет на воз­можность нового обрыва на данной кассе в следующий момент и тем более на вероятность возникновения обрыва на других кассовых аппаратах.

Для простейшего потока частота поступления требований в систему подчиняется закону Пуассона, т. е. вероятность по­ступления за время T ровно k требований задается формулой

 

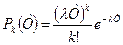, (5.1)

 

где λ — интенсивность потока заявок, т. е. среднее число заявок, поступающих в СМО в единицу времени,

 

 

, (5.2)

 

где τ — среднее значение интервала времени между двумя со­седними заявками.

 

Для такого потока заявок время между двумя соседними заяв­ками распределено экспоненциально с плотностью вероятности

 

. (5.3)

 

Случайное время ожидания в очереди начала обслуживания то­же можно считать распределенным экспоненциально:

, (5.4)

 

где ν — интенсивность движения очереди, т. е. среднее число зая­вок, приходящих на обслуживание в единицу времени,

 

, (5.5)

 

где Т_оч - среднее значение времени ожидания в очереди.

 

Выходной поток заявок связан с потоком обслуживания в кана­ле, где длительность обслуживания Т_обс является случайной величи­ной и подчиняется во многих случаях показательному закону рас­пределения с плотностью

 

, (5.6)

 

где μ — интенсивность потока обслуживания, т. е. среднее число заявок, обслуживаемых в единицу времени,

 

. (5.7)

 

Важной характеристикой СМО, объединяющей показатели λ и μ, является интенсивность нагрузки, которая показывает степень согласования указанных потоков зая­вок:

. (5.8)

 

Перечисленные показатели k, τ, λ, l_оч, Т_оч, ν, Т_обс, μ, ρ, Р_k являются наиболее общими для СМО.