Код Хаффмана
Определение 1: Пусть A={a1,a2,...,an} - алфавит из n различных символов, W={w1,w2,...,wn} - соответствующий ему набор положительных целых весов. Тогда набор бинарных кодов C={c1,c2,...,cn}, такой что:
(1) ci не является префиксом для cj, при i≠j
(2) 
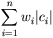минимальна (|ci| длина кода ci)
Называется минимально-избыточным префиксным кодом или иначе кодом Хаффмана.
Замечания:
1. Свойство (1) называется свойством префиксности. Оно позволяет однозначно декодировать коды переменной длины.
2. Сумму в свойстве (2) можно трактовать как размер закодированных данных в битах. На практике это очень удобно, т.к. позволяет оценить степень сжатия не прибегая непосредственно к кодированию.
3. В дальнейшем, чтобы избежать недоразумений, под кодом будем понимать битовую строку определенной длины, а под минимально-избыточным кодом или кодом Хаффмана - множество кодов (битовых строк), соответствующих определенным символам и обладающих определенными свойствами.
Известно, что любому бинарному префиксному коду соответствует определенное бинарное дерево.
Определение 2: Бинарное дерево, соответствующее коду Хаффмана, будем называть деревом Хаффмана.
Задача построения кода Хаффмана равносильна задаче построения соответствующего ему дерева. Приведем общую схему построения дерева Хаффмана:
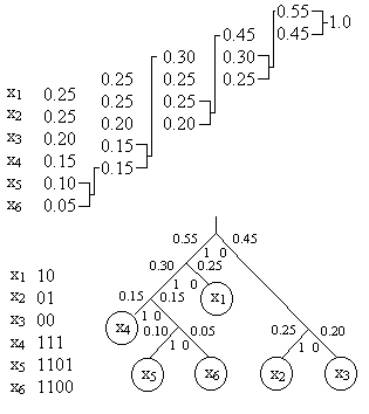
буквы располагают в порядке убывания их вероятностей. Складывают вероятности двух последних букв, и ряд переписывают снова с учетом новой вероятности (суммы). Далее повторяют операцию, пока не получится 1. Нижнюю букву всегда кодируют нулем, а верхнюю – единицей.
Для составления кодовых комбинаций строится кодовое дерево. Двигаясь по кодовому дереву сверху вниз, можно записать для каждой буквы соответствующую ей кодовую комбинацию.
Код Хаффмана, также как и Шеннона-Фано является префиксным, то есть в таком коде ни одна комбинация не совпадает с началом более длинной комбинации, а это позволяет обеспечить однозначное декодирование без введения разделительных символов.
Среднее кол-во разрядов:
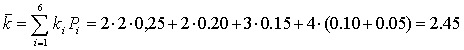
Энтропия
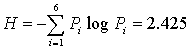
Как мы видим, величина среднего кол-ва разрядов получилась достаточно близкой к энтропии, следовательно, код можно считать эффективным. При этом для сравнения можно вычислить величину K для равномерного кода:
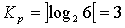
1. ЗАДАЧА.
Пусть имеется случайная величина X(x1,x2,x3,x4,x5,x6,x7,x8), имеющая восемь состояний с распределением вероятностей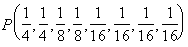 
Закодировать буквы (x1,x2,x3,x4,x5,x6,x7,x8) в коде Шеннона-Фано.
Все буквы записываются в порядке убывания их вероятностей, затем делятся на равновероятные группы, которые обозначаются 0 и 1, затем вновь делятся на равновероятные группы и т.д.
2. ЗАДАЧА
построить дерево Хаффмана для сообщения S="A H F B H C E H E H C E A H D C E E H H H C H H H D E G H G G E H C H H".
УКАЗАНИЕ: в нашем случае A={A, B, C, D, E, F, G, H}, W={2, 1, 5, 2, 7, 1, 3, 15}.
ЗАДАЧА
Пусть имеется следующая таблица префиксных кодов:
| а | л | м | р | у | ы |
| 10 | 010 | 00 | 11 | 0110 | 0111 |
Требуется декодировать сообщение: 00100010000111010101110000110
УКАЗАНИЕ: Декодирование производится циклическим повторением следующих действий:
1. отрезать от текущего сообщения крайний левый символ, присоединить к рабочему кодовому слову;
2. сравнить рабочее кодовое слово с кодовой таблицей; если совпадения нет, перейти к (1);
3. декодировать рабочее кодовое слово, очистить его;
4. проверить, имеются ли еще знаки в сообщении; если «да», перейти к (1).
ЗАДАЧА
Пусть имеется первичный алфавит A, состоящий из шести знаков a1 …a6 с вероятностями появления в сообщении, соответственно, 0,3; 0,2; 0,2; 0,15; 0,1; 0,05.
Построить код Хаффмана
ЗАДАЧА
Закодируйте двоичным кодом Шеннона-Фано ансамбль сообщений Х = х1, х2, ..., х8, если все кодируемые сообщения равновероятны. Показать оптимальный характер полученного кода.
ЗАДАЧА
Определите количество элементов в кодовом слове, если известно общее число комбинаций N = 512, а основание кода 2.
ЗАДАЧА
Сколько двоичных чисел может быть представлено 7-разрядным кодом?
ЗАДАЧА
Дана совокупность символов х1, х2, х3, х4 со следующей статистикой соответственно: 0,28; 0,14; 0,48; 0,10. Закодируйте символы по методу Шеннона-Фано и определите эффективность кода.