Оптимальное смешение
В данном разделе показаны возможности использования модели линейного программирования для задач оптимального смешения. Наряду с рассмотренной в разделе 2.1 задачей планирования производства это одна из наиболее известных областей приложения модели линейного программирования. Модели оптимального смешения имеют много общего с моделями оптимального планирования производства, но в то же время существуют и некоторые особенности.
Постановка задачи:
Необходимо определить наилучший способ смешения исходных ингредиентов для получения смеси с заданными свойствами и с наименьшими затратами.
Задачи оптимального смешения встречаются во многих отраслях промышленности (металлургия, парфюмерия, пищевая промышленность, фармакология, сельское хозяйство).
Рассмотрим однопродуктовую модель оптимального смешения.
Введем обозначения:
n - количество исходных ингредиентов;
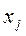m - количество компонентов в смеси;
- количество j-го ингредиента, входящего в смесь;
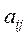
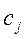- количество i-го компонента в j-м ингредиенте;
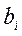- стоимость единицы j-го ингредиента;
- количество i-го компонента в смеси.
Формально задача оптимального смешения может быть описана с помощью следующей модели линейного программирования:
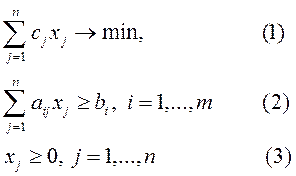
Здесь (1) – целевая функция (минимум затрат на получение смеси);
(2) – группа ограничений, определяющих содержание компонентов в смеси;
(3) – ограничения на неотрицательность переменных.
Пример 2.Рацион кормления коров на молочной ферме может состоять из трех продуктов – сена, силоса и концентратов. Эти продукты содержат питательные вещества – белок, кальций и витамины. Численные данные представлены в таблице.
| Продукты | Питательные вещества | ||
| Белок, г/кг | Кальций, г/кг | Витамины, мг/кг | |
| Сено | |||
| Силос | |||
| Концентраты |
В расчете на одну корову суточные нормы потребления белка и кальция составляют не менее 2000 и 120 г соответственно. Потребление витаминов строго дозировано и должно быть равно 87 мг в сутки.
Составить самый дешевый рацион, если стоимость 1 кг сена, силоса или концентрата равна соответственно 1,5; 2 и 6 ед.
Решение: Пусть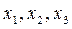 
- количество сена (г), силоса (г) и концентратов (мг) входящих в суточный рацион коровы.
Тогда этот рацион будет содержать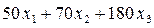 
(г) белка, 
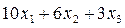(г) кальция и 
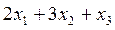(мг) витаминов. Так как содержание белка и кальция в ежедневном рационе коровы должно быть не менее 2000 и 120 г соответственно, то получим следующую систему неравенств:
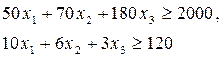(2.1)
Поскольку потребление витаминов строго дозировано, то соответствующее соотношение будет выглядеть следующим образом:
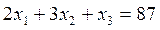(2.2)
Кроме того, переменные должны удовлетворять условию неотрицательности:
(2.3)
Так как задача состоит в составлении самого дешевого суточного рациона, следовательно, целевая функция примет вид:
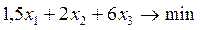(2.4)
Итак, экономико-математическая модель задачи: составить дневной рацион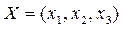 
, удовлетворяющий системе (2.1) и условиям (2.2) и (2.3), при котором функция (2.4) принимает минимальное значение.
3. Решение задачи линейного программирования с помощью Поиска решений
Поиск решения – это надстройка ЕХСЕL, которая позволяет решать оптимизационные задачи. Если в меню Сервис отсутствует команда Поиск решения, значит, необходимо загрузить эту надстройку. Выберите команду Сервис => Надстройки и активизируйте надстройку Поиск решения .Если же этой надстройки нет в диалоговом окне Надстройки, то вам необходимо обратиться к панели управления Windows, щелкнуть на пиктограмме Установка и удаление программ и с помощью программы установки ЕХСЕL (или Оffice) установить надстройку Поиск решения.
Рассмотрим пример решения задачи оптимизации плана производства четырех различных видов изделий, для изготовления которых предприятие использует три различных типа сырья. Нормы расхода сырья на производство одного изделия каждого вида, цена одного изделия, а также общее количество сырья каждого типа, которое может быть использовано предприятием, приведены в следующей таблице.
| Тип сырья | Нормы расхода сырья на производство 1 изделия | Общее количество сырья | |||
| А | В | С | D | ||
| Цена 1 изделия |
Какое количество продукции каждого вида должна выпускать компания, чтобы общая стоимость произведенной продукции была максимальной.
Составим математическую модель задачи:
Целевая функция имеет вид: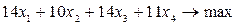 
.
Ограничения:
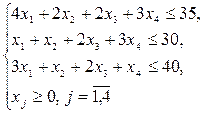
где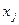 
- количество продукции j вида.
Введем условия задачи путем совершения следующих основных шагов.
1. Создание формы для ввода исходных данных задачи.
2. Ввод исходных данных.
3. Ввод зависимостей из математической модели.
4. Назначение целевой функции.
5. Ввод ограничений и граничных условий.
Для исходной задачи сделаем форму для ввода условий задачи и введем исходные данные с помощью режима формул. В задаче оптимальные значения вектора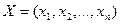 
будут помещены в ячейках ВЗ:ЕЗ,оптимальное значение целевой функции - в ячейке F5.
Введите исходные данные в созданную форму (рис.3.1).
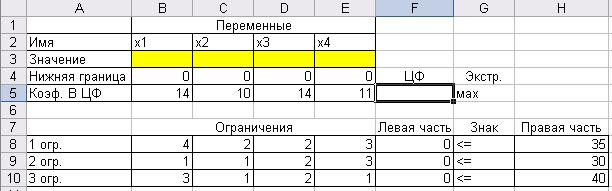
Рис. 3.1 Исходная форма для решения ЗЛП
Ввод зависимости для целевой функции.
· Курсор в F5.
· Выбираем кнопку мастер функций.
· В окне КАТЕГОРИЯ выделяем категорию МАТЕМАТИЧЕСКИЕ.
· В окне ФУНКЦИИ выбираем СУММПРОИЗВ.
· В Массив 1 введите В3:E3(рис. 3.2).
· В Массив 2 введите В5:E5(рис. 3.2).
· ОК. В ячейке F5появится значение 0.
Рис. 3.2 Диалоговое окно МАСТЕР ФУНКЦИЙ
Ввод зависимостей для левых частей ограничений производим по аналогии.
На этом ввод данных в таблицу закончен (рис. 3.3).
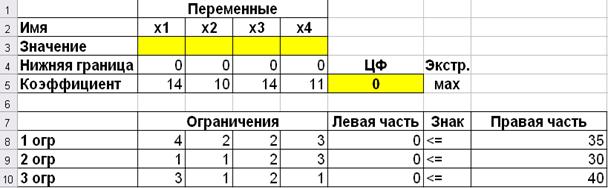
Рис 3.3 Ввод исходных данных
Далее работаем в диалоговом окне ПОИСК РЕШЕНИЯ (меню СЕРВИС – ПОИСК РЕШЕНИЯ…).
Назначение целевой функции:
· В окне УСТАНОВИТЬ ЦЕЛЕВУЮ ЯЧЕЙКУ вводим адрес F5.
· Выберем направление изменения целевой функции: максимальному значению.
Ввод ограничений и граничных условий проводим при помощи курсора Добавить…
На экране появится диалоговое окно ДОБАВЛЕНИЕ ОГРАНИЧЕНИЯ (рис. 3.4). Введем граничные условия и ограничения на переменные.
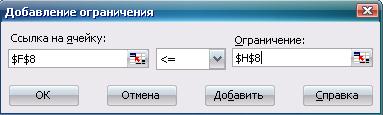
Рис. 3.4 диалоговое окно ДОБАВЛЕНИЕ ОГРАНИЧЕНИЯ
После ввода последнего ограничения вместо Добавить… выбираем ОК. В результате на экране появилось диалоговое окно ПОИСК РЕШЕНИЯс введенными условиями (рис. 3.5).
Рис. 3.5 Диалоговое окно Поиск решения
Таким образом, условия задачи введены. Далее следует приступить к решению.
Решение задачи производится сразу же после ввода данных в диалоговом окне ПОИСК РЕШЕНИЯ.
1. Выбираем кнопку ПАРАМЕТРЫ… На экране появится диалоговое окно ПАРАМЕТРЫ ПОИСКА РЕШЕНИЯ (рис. 3.6).
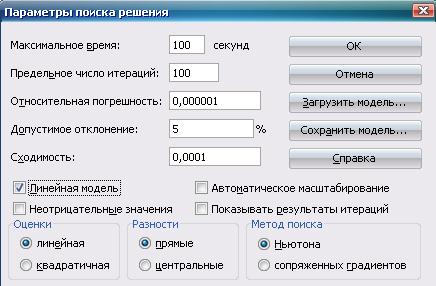
Рис 3.6 диалоговое окно Параметры поиска решения
С помощью команд, находящихся в этом диалоговом окне, можно вводить условия для решения задач оптимизации всех классов. Команды, используемые по умолчанию, подходят для решения большей части практических задач.
Устанавливаем флажок ЛИНЕЙНАЯ МОДЕЛЬ, что обеспечит применение симплекс-метода. Нажимаем ОК.
На экране появляется диалоговое окно ПОИСК РЕШЕНИЯ (рис. 3.5).
2. Выбираем кнопку ВЫПОЛНИТЬ.
На экране появляется диалоговое окно Результаты поиска решения (рис. 3.7).
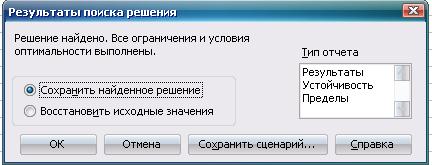
Рис. 3.7 Диалоговое окно Результат поиска решения
Если решение не найдено, окно выведет соответствующее сообщение.
Если решение найдено, выделим все три типа отчетов (Результаты, Устойчивость, Пределы), нажмем ОК. На экране – результаты решения задачи (рис. 3.8).
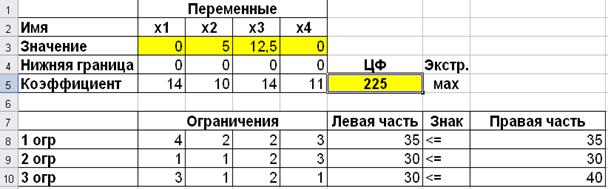
Рис. 3.8 Результаты решения задачи
Для анализа полученного оптимального решения в Еxcel предусмотрены три типа отчетов: отчет по результатам, устойчивости, пределам.
В отчете по результатам приведены сведения о целевой функции, значениях искомых переменных и результаты оптимального решения для ограничений (рис. 3.9).
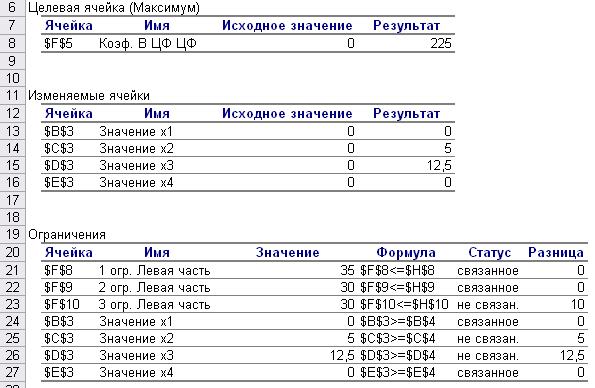
Рис. 3.9 Отчет по результатам
Для ограничений в столбце Формула приведены зависимости, которые были введены в диалоговое окно ПОИСК РЕШЕНИЯ; в столбце Значение – величины использованного ресурса; в столбце Разница – количество неиспользованного ресурса. Если ресурс расходуется полностью, то в столбце Статус указывается «связанное»; при неполном использовании ресурса в этом столбце указывается «не связан». Для переменных показывается разность между значениями переменных в найденном оптимальном решении и заданным для них граничным условием.
В отчете по устойчивости (рис. 3.10) дан анализ по переменным и ограничениям. Исследование устойчивости оптимального решения – это изучение влияния изменений отдельно взятых параметров модели (оценок целевой функции, технико-экономических коэффициентов, объемов ограничений по ресурсам и продуктам, значений базисных переменных и др.) и ее структуры (введение новых ограничений и переменных или их сокращение) на показатели оптимального решения. Такой анализ позволяет судить о пределах допустимых изменений в оптимальном плане и о его устойчивости.
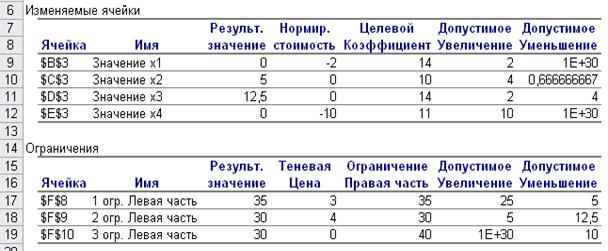
Рис. 3.10 Отчет по устойчивости
В результате решения в разделе Изменяемые ячейки приведены следующие данные:
· результирующие значения переменных;
· нормированная стоимость, т. е. дополнительные двойственные переменные, которые показывают, насколько изменяется значение целевой функции при принудительном включении единицы этой переменной в оптимальное решение;
· коэффициенты целевой функции;
· допустимые значения приращения коэффициентов целевой функции, при которых сохраняется набор переменных, входящих в оптимальное решение.
В разделе Ограничения приведены значения:
· величин используемых ресурсов;
· теневые цены, т. е. двойственные оценки, которые показывают, как изменится целевая функция при изменении ресурсов на единицу;
· значения приращения ресурсов, при которых сохраняется оптимальный набор двойственных переменных, входящих в оптимальное решение.
В отчете по пределам (рис. 3.11) показано, в каких пределах может изменяться выпуск продукции, вошедшей в оптимальное решение, при сохранении структуры оптимального решения.
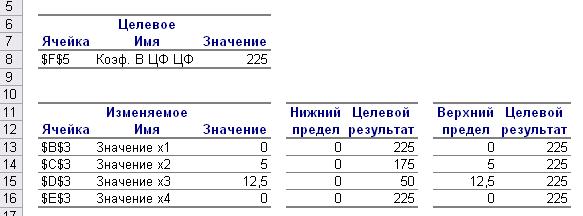
Рис. 3.11 Отчет по пределам
Выводы
На основе Отчета по результатам можно сделать следующие выводы об оптимальном решении поставленной задачи:
· максимальное значение прибыли от продажи производимых товаров составляет 225 тыс. руб.;
· оптимальный план предусматривает производство товаров В и С в количестве 5 и 12,5 шт. соответственно;
· для того чтобы, продукты 1 и 4 вида вошли в оптимальный план производства необходимо увеличить цену этих продуктов на 2 и 10 руб. соответственно (нормированная стоимость);
· ресурсы 1 и 2 типов расходуются полностью, и остается неиспользованным 10 ед. сырья 3 типа. Следовательно, ресурсы 1 и 2 типа являются дефицитными.
Согласно Отчету по устойчивости можно сделать следующие выводы:
· интервал возможного изменения значений коэффициентов целевой функции, при которых сохраняется текущее оптимальное решение, следующие: товар А: [14-0; 14+2]
товар В: [10-0,67; 10+4]
товар С: [14-4; 14+2]
товар D: [11-0; 11+10];
· двойственные оценки (теневые цены) 1 и 2 типов ресурсов положительные. Это еще раз подтверждает, что ресурсы 1 и 2 типа являются дефицитными. Двойственная оценка 1 типа ресурсов показывает, что при его изменении на 1 единицу значение целевой функции измениться на 3 единицы. Аналогично двойственная оценка 2 типа ресурсов, показывает изменение значения целевой функции на 4 единицы, при изменении ресурса 2-ого типа на 1 единицу. Следовательно, наиболее предпочтительным (с точки зрения увеличения запаса ресурсов) из дефицитных ресурсов является ресурс 2 типа, поскольку его изменение обеспечивает наибольший прирост целевой функции.
· интервалы изменения объемов используемых ресурсов, при которых сохраняется текущие оптимальные двойственные оценки, следующие:
1 тип ресурсов: [35-5; 35+25]
2 тип ресурсов: [30-12,5; 30+5]
3 тип ресурсов: [40-10; 40+0]
Изменение количества ресурсов за пределами интервалов устойчивости приводит к новым оценкам ресурсов. Так, увеличение ресурса 2 типа на 10 ед. не приведет к увеличению целевой функции на 10*4=40 руб., поскольку двойственная оценка будет иметь другое значение
Литература
1) Акулич И. Л. Математическое программирование в примерах и задачах: Учеб. Пособие для студентов эконом. спец. вузов. – М.: Высш. шк., 1986. – 319 с., ил.
2) Афанасьев М. Ю., Суворов Б. П. Исследование операций в экономике: модели, задачи, решения: Учеб. пособие. – М.: ИНФРА-М, 2003. – 244с. – (Серия «Высшее образование»).
3) Бережная Е. В., Бережной В. И. Математические методы моделирования экономических систем: Учеб. пособие. – М.: Финансы и статистика, 2001. – 368 с.: ил.
4) Исследование операций в экономике: Учебн. пособие для вузов/ Н. Ш. Кремер, Б. А. Путко, И. М. Тришин, М. Н. Фридман; Под ред. проф. Н. Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 1999. – 407 с.
5) Маркин Ю. П. Математические методы и модели в экономике: Учеб. Пособие/ Ю. П. Маркин. – М.: Высш. шк., 2007. – 422 с.
6) Решение оптимизационных задач в экономике / А. В. Каплан [и др.]. – Ростов н/Д: Феникс, 2007. – 541, [1] с.: ил. – («Высшее образование»).
7) Таха Х. Введение в исследование операций. Т. 1. М.: Мир, 1895. – 479 с.