Вопрос Комплексные числа и действия над ними

Комплексным числом z называется пара (x, y) действительных чисел x и y. При этом равенство, сумма и произведение упорядоченных пар, а также отождествление некоторых из них с действительными числами определяются следующим образом:

1) два комплексных числа z₁ = (x₁, y₁) и z₂ = (x₂, y₂) называются равными, если x₁ = x₂ и y₁ = y₂;

2) суммой комплексных чисел z₁ и z₂ называется комплексное число z вида

z = (x₁ + x₂, y₁ + y₂);

3) произведением комплексных чисел z₁ и z₂ называется комплексное число

z = (x₁x₂ - y₁y₂, x₁y₂ + x₂y₁);

4) множество комплексных чисел 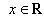, отождествляется с множеством действительных чисел R.

Разностью комплексных чисел z₁ и z₂ называется комплексное число z такое, что z₂ + z = z₁, откуда находим z = z₁ - z₂ = (x₁ - x₂,y₁ - y₂).

Частным комплексных чисел z₁ и z₂ называется комплексное число z такое, что . Отсюда находим

Комплексное число (0, 1) обозначается символом i = (0, 1). Тогда , т. е. i² = -1. Произвольное комплексное число z можно записать в виде

z = (x, y) = (x, 0) + (0, y) = (x, 0) + (0, 1)(y, 0) = x + iy.

Эта запись называется алгебраической формой комплексного числа. Комплексное число называетсясопряженным по отношению к комплексному числу z = (x, y) = x + iy.