Теорема 1. (Формула включения и исключения)

Доказательство. По индукции. При n=1, 2 утверждение очевидно. Заметим, что имеет место соотношение 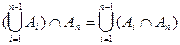. Предположим, что для n-1 множеств утверждение верно. Тогда

= .

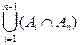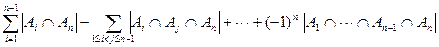Откуда

Следовательно, утверждение верно для n множеств. Что и требовалось доказать.

Задача о встречах. В дождливую погоду n человек пришли в театр. Они сдают зонтики в гардероб. После окончания спектакля получают зонтики обратно, в случайном порядке. Какова вероятность того, что каждый из них получит чужой зонтик?

Задача сводится к нахождению числа перестановок элементов множества {1, 2, ∙ ∙ ∙ , n}, не имеющих неподвижных точек.

Пусть S_i состоит из перестановок, оставляющих неподвижной точку i. Вычислим | S₁È S₂ È ∙ ∙ ∙È S_n |.

Искомая вероятность будет равна .

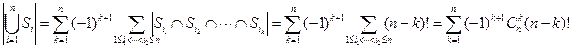
Получаем . Отсюда число перестановок, не имеющих неподвижных точек, равно . Искомая вероятность равна . Число f(n) будет ближайшим к дроби целым числом. При n®¥ вероятность стремится к .

Задача о счастливых билетах. Требуется найти число решений уравнения x₁+x₂+x₃ = y₁+y₂+y₃ , где 0 £ x_i , y_i £ 9.

1) Подстановка x₄=9-y₁ , x₅=9-y₂ , x₆=9-y₃ устанавливает биекцию между решениями этого уравнения и уравнения x₁+x₂+x₃ + x₄+x₅+x₆ = 27, где 0£ x_i £9.

Найдем число разложений x₁+x₂+x₃ + x₄+x₅+x₆ = 27, где 0£ x_i £9.

Пусть U₁ – число разложений с x₁³10,

U₂ – число разложений с x₂³10,

∙∙∙

U₆ – число разложений с x₆³10.

Тогда | U_i ÇU_jÇU_k | =0 при |{I,j,k}|=3.

Вычислим число разложений, не удовлетворяющих неравенствам 0£ x_i £9. Оно равно

| U₁ ÈU₂ÈU₃ ÈU₄ ÈU₅ ÈU₆ | = 6|U₁|─15|U₁ÇU₂|,

где | U₁| ─ число решений уравнения (x₁─10)+x₂+x₃ + x₄+x₅+x₆ = 27─10,

а |U₁ÇU₂| ─ число решений уравнения

(x₁─10)+(x₂─10)+x₃ + x₄+x₅+x₆ = 27─10-10.

Получаем | U₁ ÈU₂ÈU₃ ÈU₄ ÈU₅ ÈU₆ | = .

Из числа всех разложений вычитаем разложения с x_i ≥10. Получаем окончательный ответ

.

Функция Эйлера. Пусть n – положительное натуральное число, j(n) – количество натуральных чисел 0<d£n , взаимно простых c n. Например, при n=10, dÎ{1, 3, 7, 9} и j(10) = 4 . Функция j(n) называется функцией Эйлера.