Свойства отношения порядка

Для любых действительных чисел a и b: или a≤b, или a≥b. При этом выполняются следующие свойства:

1) Свойство полноты

∀a,b∈R справедливо одно из трёх: a=b, a>b(b<a), a<b(b>a).

Для любых действительных чисел a и b справедливо одно из трёх утверждений: либо a и b равны, либо a больше b (b меньше a), либо a менше b (b больше a).

2) Рефлексивность

∀a∈Ra≤a.

Для любого действительного числа a: a меньше либо равно a.

3) Свойство тождества

∀a,b∈Ra≤bиa≥b⇒a=b.

Если для двух любых действительных чисел a и b выполняется условие a меньше либо равно b и b меньше либо равно a, то a и b равны.

4) Транзитивность

∀a,b,c∈Ra≤bиb≤c⇒a≤c.

Для любых действительных чисел a, b, c: если a меньше либо равно b и b меньше либо равно c, то a меньше либо равно c.

5) Сохранение неравенства

∀a,b,c∈Ra≤b⇒a+c≤b+c.

Для любых действительных чисел a, b, c, в случае выполнения неравенства aменьше либо равно b, при прибавлении к обоим частям неравенства одного и того же числа c знак неравенства остаётся прежним.

6) Правило знаков

∀a,b∈Ra≥0иb≥0⇒a⋅b≥0.

Произведение двух любых положительных действительных чисел положительно.

5. Аксиома Архимеда.

∀a∈R∃n∈Na≤n

6. Теорема (аксиома) Дедекинда.

Пусть заданы два множества A и B - не пустые, не пересекающиеся и в объединении дающие множество действительных чисел: A≠∅,B≠∅,A∩B=∅,A∪B=R. И пусть ∀a∈A∀b∈Ba<b, тогда существует такое действительное число c, для которого выполняется следующее условие: a≤c≤b.

О множествах A и B говорят, что они образуют Дедекиндово сечение, а число c это сечение производит. Это число c принадлежит либо множеству A, тогда в множестве A есть наибольшее число, а в множестве B нет наименьшего числа, либо c принадлежит множеству B, тогда в множестве B оно наименьшее, а в множестве Aнет наибольшего. Ясно, что число c, осуществляющее Дедекиндово сечение, единственно. Теорема Дедекинда формулирует свойство полноты (или непрерывности) множества действительных чисел.

 

24. Множество действительных чисел

Если множество рациональных чиселдополнить множеством иррациональных чисел, то вместе они составят множество действительных чисел. Множество действительных чисел обычно обозначают буквой R; используют также символическую запись (-оо, +оо) или (-оо, оо).

Множество действительных чисел можно описать так: это множество конечных и бесконечных десятичных дробей; конечные десятичные дроби и бесконечные десятичные периодические дроби — рациональные числа, а бесконечные десятичные непериодические дроби — иррациональные числа.

Каждое действительное число можно изобразить точкой на координатной прямой. Верно и обратное: каждая точка координатной прямой имеет действительную координату. Математики обычно, говорят так: между множеством R действительных чисел и множеством точек координатной прямой установлено взаимно однозначное со ответствие. Координатная прямая есть геометрическая модель множества действительных чисел; по этой причине для координатной прямой часто используют термин числовая прямая.

Вдумайтесь в этот термин: не кажется ли он вам противоестественным? Ведь число — объект алгебры, а прямая — объект геометрии. Нет ли тут «смешения жанров»? Нет, все логично, все продумано. Этот термин в очередной раз подчеркивает единство различных областей математики, дает возможность отождествления понятий «действительное число» и «точка на координатной (числовой) прямой».

Обратите внимание: координатной прямой вы пользовались начиная с 5-го класса. Но, оказывается, в ваших знаниях был вполне оправданный пробел: не для любой точки координатной прямой вы сумели бы найти координату — просто учитель оберегал вас от такой неприятности.

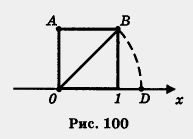
Рассмотрим пример. Дана координатная прямая, на ее единичном отрезке построен квадрат (рис. 100), диагональ квадрата ОВ отложена на координатной прямой от точки О вправо, получилась точка D. Чему равна координата точки D? Она равна длине диагоналиквадрата, т. е. 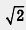. Это число, как мы теперь знаем, не целое и не дробь. Значит, ни в 5-м, ни в 6-м, ни в 7-м классе координату точки D вы бы найти не смогли.

Потому мы до сих пор и говорили «координатная прямая», а не «числовая прямая».

Заметим, что был еще один оправданный пробел в ваших знаниях по алгебре. Рассматривая выражения с переменными, мы всегда подразумевали, что переменные могут принимать любые допустимые значения, но только рациональные, ведь других-то не было. На самом деле переменные могут принимать любые допустимые действительные значения. Например, в тождестве (а + Ь){а-b) = а²-b² в роли а и b могут выступать любые числа, не обязательно рациональные. Этим мы уже пользовались в конце предыдущего параграфа. Этим же мы пользовались и в § 18 — в частности, в примерах 6, 7, 8 из указанного параграфа.

Для действительных чисел а, b, с выполняются привычные законы:

а + b = b + а;

аЬ = bа;

a + (b + c) = (a + b) + c

a(bc) =(ab)c

(а + b) с = ас + bc и т. д.

Выполняются и привычные правила: произведение (частное) двух положительных чисел — положительное число;
произведение (частное) двух отрицательных чисел — положительное число; произведение (частное) положительного и отрицательного числа — отрицательное число.

Действительные числа можно сравнивать друг с другом, используя следующее определение.

Определение. Говорят, что действительное число а больше (меньше) действительного числа b, если их разность а - b — положительное (отрицательное) число. Пишут а > b (а < b).

Из этого определения следует, что всякое положительное число а больше нуля (поскольку разность а - 0 = а — положительное число), а всякое отрицательное число b меньше нуля (поскольку разность b - 0 = b — отрицательное число).

Итак, а > 0 означает, что а — положительное число;

а < 0 означает, что а — отрицательное число;
а>b означает, что а -b — положительное число, т. е. а - b > 0;
a<b означает, что а - b — отрицательное число,
т.е. а - b < 0.

Наряду со знаками строгих неравенств (<, >) используют знаки нестрогих неравенств:

а 0 означает, что а больше нуля или равно нулю, т. е. а — неотрицательное число (положительное или 0), или что а не меньше нуля;

а 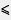0 означает, что а меньше нуля или равно нулю, т. е. а — неположительное число (отрицательное или 0), или что а не больше нуля;

а b означает, что а больше или равно b, т. е. а - b — неотрицательное число, или что а не меньше b; а - b 0;

а 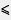b означает, что а меньше или равно b, т. е. а - b — неположительное число, или что а не больше Ь; а - b 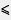0.
Например, для любого числа а верно неравенство а² 0;

для любых чисел а и b верно неравенство (а - b)² 0.
Впрочем, для сравнения действительных чисел необязательно каждый раз составлять их разность и выяснять, положительна она или отрицательна. Можно сделать соответствующий вывод, сравнивая записи чисел в виде десятичных дробей.

Геометрическая модель множества действительных чисел, т. е. числовая прямая, делает операцию сравнения чисел особенно наглядной: из двух чисел а, b больше то, которое располагается на числовой прямой правее.

Таким образом, к сравнению действительных чисел нужно подходить достаточно гибко, что мы и используем в следующем примере.

Пример 1. Сравнить числа:

Пример 2. Расположить в порядке возрастания числа

 

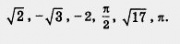
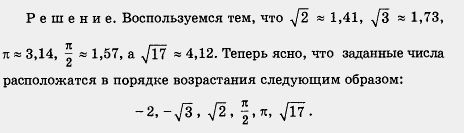
23. Рациональные числа - это целые и дробные числа (обыкновенные дроби, конечные десятичные дроби и бесконечные периодические дроби).

Есть версия, что название рациональных чисел связано с латинским словом «ratio» - разум.

 

Бесконечные непериодические дроби НЕ входят в множество рациональных чисел.

Поэтому число «Пи» (π = 3,14...), основание натурального логарифма
e (e = 2,718..) или √2 НЕ являются рациональными числами.

Примеры рациональных чисел:

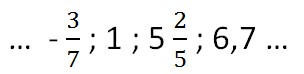
Множество рациональных чиселобозначается заглавной английской буквой Q (кью).

Множество Q включает в себя множество целых чисел (Z) и натуральных чисел (N).

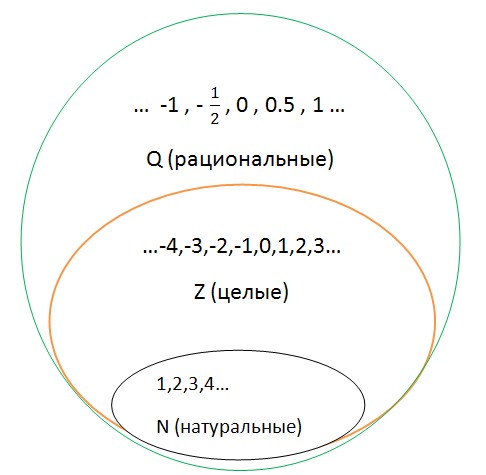
Любое рациональное число можно представить в виде дроби, у которой числитель принадлежит целым числам, а знаменатель - натуральным.
^a/_b, где a ∈ Z ( a принадлежит целым числам ), b∈N ( b принадлежит натуральным числам ).

 

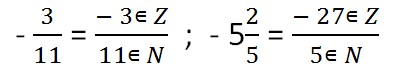
22. Сложение и вычитание десятичных дробей. Эти операции выполняются так же, как и сложение и вычитание целых чисел. Необходимо только записать соответствующие десятичные знаки один под другим.

П р и м е р .

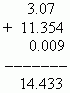
Умножение десятичных дробей. На первом этапе перемножаем десятичные дроби как целые числа, не принимая во внимание десятичную точку. Затем применяется следующее правило: количество десятичных знаков в произведении равно сумме десятичных знаков во всех сомножителях.

Замечание: до простановки десятичной точки в произведении нельзя отбрасывать нули в конце!

П р и м е р .

Сумма чисел десятичных знаков в сомножителях равна: 3 + 4 = 7. Сумма цифр в произведении равна 6. Поэтому необходимо добавить один ноль слева: 0197056 и проставить перед ним десятичную точку: 0.0197056.