Сопряженные комплексные числа.

Определение. Два комплексных числа, имеющие одну и ту же действительную часть и взаимно противоположные коэффициенты мнимых частей, называются взаимно) сопряженными.

Для любого комплексного числа z существует одно и только одно сопряженное с ним комплексное число, которое обозначается . Если , то . Очевидно, 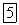тогда и только тогда, когда z — действительное число.

Отметим, что сумма и произведение двух сопряженных комплексных чисел являются действительными числами:

Ранее было выведено правило деления комплексных чисел. Это правило можно проще получить с помощью сопряженных комплексных чисел.

Умножим числитель и знаменатель дроби — на число комплексно сопряженное со знаменателем. Выполнив действия и отделив действительную часть от мнимой, получаем:

Этот результат совпадает с формулой, полученной в п. 6.

Эту формулу можно не запоминать, а только помнить, что при делении надо числитель и знаменатель дроби умножить на число, комплексно сопряженное со знаменателем.

Теорема 1. Число, сопряженное с суммой или произведением комплексных чисел, есть сумма или соответственно произведение чисел, сопряженных данным комплексным числам:

Доказательство. Пусть . Тогда . Имеем:

Точно так же

Эта теорема показывает, что, поставив в соответствие каждому комплексному числу сопряженное с ним число, мы получили взаимно однозначное отображение поля комплексных чисел К на это же поле при котором сохраняются операции сложения и умножения.

Из теоремы 1 непосредственно вытекает следующее

Следствие 1. Число, сопряженное (натуральной) степени комплексного числа, равно той же степени числа, сопряженного данному:

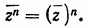
Далее, если нам дан многочлен

коэффициенты которого — комплексные числа, то, заменив каждый коэффициент сопряженным ему комплексным числом мы получим новый многочлен, который обозначим через

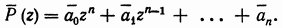
Если теперь в полученном многочлене произвольное значение переменной заменить сопряженным ему значением то в силу доказанной выше теоремы и следствия I полученное значение многочлена будет комплексным числом, сопряженным с исходным значением многочлена

Если, в частности, все коэффициенты многочлена действительные числа, то один и тот же многочлен, и формула (3) дает:

Таким образом, мы получили

Следствие 2. При замене в многочлене с действительными коэффициентами произвольного значения аргумента сопряженным ему числом значение многочлена также заменяется сопряженным ему числом.

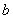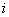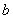30. Комплексным числом называется число вида , где и – действительные числа, – так называемая мнимая единица. Число называется действительной частью ( )комплексного числа , число называется мнимой частью ( ) комплексного числа .

– это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами: или переставить мнимую единицу: – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке:

Чтобы всё было понятнее, сразу приведу геометрическую интерпретацию. Комплексные числа изображаются на комплексной плоскости:

Как упоминалось выше, буквой 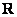принято обозначать множество действительных чисел.Множествожекомплексных чиселпринято обозначать «жирной» или утолщенной буквой . Поэтому на чертеже следует поставить букву , обозначая тот факт, что у нас комплексная плоскость.

Комплексная плоскость состоит из двух осей:
– действительная ось
– мнимая ось

Правила оформления чертежа практически такие же, как и для чертежа в декартовой системе координат (см. Графики и свойства элементарных функций). По осям нужно задать размерность, отмечаем:

ноль;

единицу по действительной оси;

мнимую единицу 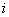по мнимой оси.

Не нужно проставлять все значения: …–3, –2, –1, 0, 1, 2, 3,… и .

Да чего тут мелочиться, рассмотрим чисел десять.

Построим на комплексной плоскости следующие комплексные числа:
, ,
, ,
, , ,

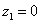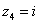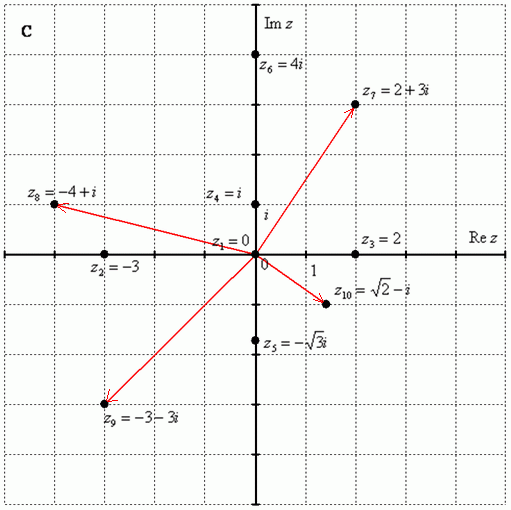
По какому принципу отмечены числа на комплексной плоскости, думаю, очевидно – комплексные числа отмечают точно так же, как мы отмечали точки еще в 5-6 классе на уроках геометрии.

Рассмотрим следующие комплексные числа: 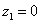, , . Вы скажете, да это же обыкновенные действительные числа! И будете почти правы. Действительные числа – это частный случай комплексных чисел. Действительная ось обозначает в точности множество действительных чисел 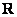, то есть на оси сидят все наши «обычные» числа. Более строго утверждение можно сформулировать так: Множество действительных чисел 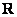является подмножеством множества комплексных чисел .

Числа 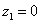, , – это комплексные числа с нулевой мнимой частью.

Числа 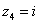, , – это, наоборот, чисто мнимые числа, т.е. числа с нулевой действительной частью. Они располагаются строго на мнимой оси .

В числах , , , и действительная и мнимая части не равны нулю. Такие числа тоже обозначаются точками на комплексной плоскости, при этом, к ним принято проводить радиус-векторы из начала координат (обозначены красным цветом на чертеже). Радиус-векторы к числам, которые располагаются на осях, обычно не чертят, потому что они сливаются с осями.