Графиктер

Әр түрлі екі шаманың арасындағы тәуелділік координатаның жазықтықта сызықпен кескінделеді, оны график деп атайды.

 

Мысалы, Автомашинаның жүрген уақыты мен жолының арасындағы тәуелділік.

 

Уақыт пен сол уақытқа сәйкес ауа температурасы арасындағы тәуелділік.

Функция туралы ұғым. Функцияның формуламен берілуі

Күнделікті өмірде бір шаманың мәні екінші шаманың мәніне тәуелді болады.

Мысалы: заттың құны мен бағасы, жүрілген жол уақытқа немесе жылдамдыққа тәуелді.

 

Тәуелсіз шаманы аргумент деп атайды, ал тәуелді шаманы функция деп атайды.

 

Тәуелсіз айнымалының әрбір мәніне тәуелді айнымалының бір ғана мәні сәйкес келетін тәуелділікті функция деп атайды.

 

Функция формуламен, кестемен немесе графикпен беріледі.

 

Функция жазылуының жалпы түрі у = f(х) оқылуы «у тең икстен эф».

 

Мұндағы х – аргумент, у – функция, ал f – функцияның аргументке тәуелділігін білдіретін таңба.

 

 

Тәуелсіз айнымалының қабылдайтын мәндерінің жиыны функцияның анықталу аймағы деп аталады.

 

Мысалы: анықталу аймағы 2-ден басқа сандар, себебі х = 2 болса, бөлшек бөлімі 0 болып, анықталмайды, яғни .

 

Функцияның мәндер жиынын функцияның мәндер аймағы деп атайды.

Функцияның кестемен берілуі

Тәжірибелер мен сынақ нәтижелері аргумент пен оған сәйкес функция мәндері белгілі бір ретпен кесте арқылы беріледі.

 

Мысалы: Бір тәуліктегі температураның өзгерісі:

 

уақыт

температура

–3

–2

–1

–2

 

Функцияның графикпен берілуі

Функцияның графигі деп координаталық жазықтықта абсциссалары аргумент мәндері, ал ординаталары функция мәндері болатын нүктелер жиынын атайды.

 

Графикті пайдаланып аргументтің берілген мәніндегі функцияның мәнін табу үшін:

1. аргумент мәнін абсцисса осімен тауып, оған перпендикуляр түзу жүргізу керек;

2. оның графикпен қиылысқан нүктесінен ордината осьіне перпендикуляр жүргізу керек;

3. осы перпендикулярдың ордината осімен қиылысуындағы сан функцияның мәнін береді.

Ал функцияның берілген мәні бойынша аргументті табу үшін осы алгоритмді кері орындау керек.

 

Сызықтық функция және оның графигі

у = kx + l (мұндағы x – тәуелсіз айнымалы, k және l – қандай бір сандар) формуласымен берілген функция сызықтық деп аталады.

 

 

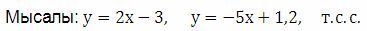
Сызықтық функцияның графигі түзу сызық болады.

Сызықтық функцияның графигі түзу болғандықтан екі нүктенің координатасын тауып, түзу салу керек.

 

Ол нүктенің бірі ретінде абсциссасы 0-ге тең нүктені алған тиімді.

Мысалы: 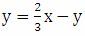функциясының графигін салайық. Ол үшін х = 0, у = – 4, яғни А(0; – 4) х = 3, х = –2, яғни В (3; –2) осы нүктелерді координаталық жазықтықта белгілеп, осы нүктелер арқылы түзу сызу жеткілікті.

 

Берілген нүктенің түзуге тиісті немесе тиісті болмауын анықтау үшін нүктенің координаталары х пен у-тың орнына қойып, дұрыс теңсіздік шығатынын тексеру керек.

 

Мысалы: у = 2х + 3 функциясының графигіне А(–1; 1) және В(2; 5) нүктелерінің тиісті болатынын не болмайтынын анықтайық. Ол үшін:

Сызықтық функцияның дербес жағдайлардағы графигі

у = kx+l функциясында l = 0 болса, онда у = kx түрінде болады.

 

у = kx формуласымен берілген функцияны тура пропорционалдық деп аталады.

Мысалы: у = 2x; у = kx тура пропорционалдығының графигі – координаталар басы арқылы өтетін түзу болса, І, ІІІ ширекте, 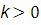болса, ІІ, ІV ширекте жатады.

 

k = 0 болса, онда у = l тұрақты функция болады, оның графигі ОХ осіне параллель түзулер.

 

Егер k мәндері тең болса, у = kx және у = kx+l түзулері өзара параллель болып орналасады.

Сызықтық функциялар графиктерінің орналасуы

Бір координаталық жазықтықта орналасқан екі сызықтық функциялардың графиктері қиылысу үшін бұрыштық коэффициенттері (х-тың алдындағы коэффициент) тең болмауы керек.

Егер сызықтық функциялардың бұрыштық коэффициенттері тең болса, онда олардың графиктері параллель болатын түзулер болады.

 

 

Екі айнымалысы бар сызықтық теңдеу

ax + bc = c түріндегі теңдеулер екі айнымалысы бар сызықтық теңдеулер деп аталады, мұндағы х пен у – айнымалылар, а, в және с – сандар.

Сызықтық теңдеулердегі а, в – коэффициенттер, ал с – бос мүше деп аталады.

 

Екі айнымалысы бар сызықтық теңдеуді тура теңдікке айналдыратын айнымалылардың мәндерінің жұбы осы теңдеудің шешімі деп аталады.

 

Мысалы: х + 5у = 6 теңдеуіне шешім болатын сандар жұбы (1; 1), (0; 1,2), (6; 0) т.с.с.

Екі айнымалысы бар сызықтық теңдеудің графигі

Координаталық жазықтықтағы координаталары теңдеудің шешімдері болатын нүктелер жиыны екі айнымалысы бар теңдеудің графигі деп аталады.

Екі айнымалысы бар сызықтық теңдеулер жүйелері. Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу

Екі айнымалысы бар екі теңдеудің ортақ шешімін табу үшін біріктірілуін теңдеулер жүйесі дейміз. Бір жүйеге біріктірілген теңдеулер фигуралық жақшамен жазу қабылданған.

Екі айнымалысы бар сызықтық теңдеулер жүйесіндегі теңдеулердің әрқайсысын тура теңдікке айналдыратын айнымалылардың мәндерінің жұбын сол теңдеулер жүйесінің шешімі деп атайды.

 

Екі айнымалысы бар сызықтық теңдеулер жүйесін шешудің графиктік, алмастыру, қосу тәсілдері бар.

 

Графиктік тәсілмен шешуде мынандай үш жағдай кездеседі:

1. теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер өзара қиылысады. Мұндай жағдайда теңдеулер жүйесінің шешімін табу үшін:

o жүйедегі теңдеулердің әрқайсысының графигін салу керек;

o олардың қиылысу нүктесінің координаталарын табу керек.

Осы нүктенің координаталары теңдеулер жүйесінің шешімі болады.

 

Түзулердің қиылысу нүктесі біреу ғана болғандықтан бұл жағдайдағы теңдеулер жүйесінің шешімі біреу ғана болады.

1. Теңдеулер жүйесіндегі теңдеулердің графиктері болатын түзулер өзара параллель болғанда қиылысу нүктесі табылмайды, яғни бұл жағдайда теңдеулер жүйесінің шешімі жоқ.

Жүйедегі теңдеулердің графигі болатын түзулер беттеседі. Бұл жағдайда ортақ шексіз көп нүкте табылады, яғни теңдеулер жүйесінің шексіз көп шешімі болады.

Екі айнымалысы бар сызықтық теңдеулер жүйесін алмастыру тәсілімен шешу

Екі айнымалысы бар сызықтық теңдеулер жүйесін алмастыру тәсілімен шешу үшін:

1. Теңдеудің біреуіндегі бір айнымалыны екінші айнымалы арқылы өрнектеу керек;

2. Табылған өрнекті екінші теңдеудегі осы айнымалының орнына қою керек. Сонда бір айнымалысы бар сызықтық теңдеу шығады;

3. Шыққан сызықтық теңдеуді шешіп, айнымалының мәнін табу керек;

4. Табылған айнымалының мәнін екінші айнымалыны табу өрнегіндегі орнына қойып, екінші айнымалыны табу керек.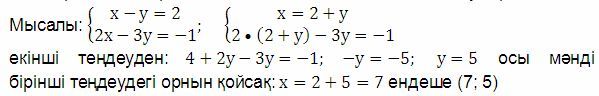

Екі айнымалысы бар сызықтық теңдеулер жүйесін қосу тәсілімен шешу

Екі айнымалысы бар сызықтық теңдеулер жүйесін қосу тәсілімен шешу үшін:

1. Жүйедегі теңдеулердің айнымалылардың біреуінің коэффициенттері қарама-қарсы сандар болатындай әр теңдеуді көбейткіштерге көбейту керек;

2. Жүйедегі теңдеулерді мүшелеп қосып, бір айнымалысы бар теңдеуге айналдыру керек;

3. Шыққан теңдеуді шешіп, айнымалының мәнін табу керек;

4. Осы айнымалының мәнін жүйедегі бір теңдеудегі орнына қойып, екінші айнымалының мәнін табу керек.

 

Жүйедегі теңдеулердің біреуіндегі 2х – у = 15 у-тің орнына мәнін қойсақ, 2х – 7 = 15, 2х = 22, х = 11.

Жауабы: (11; 7)

Бір айнымалысы бар сызықтық теңсіздіктер жүйесін шешу

Бір айнымалысы бар екі немесе бірнеше теңсіздіктердің шешімдері ортақ болған жағдайда, оларды бір жүйеге біріктіріп жазуға болады.

 

Бір айнымалысы бар теңсіздіктер жүйесінің шешімі дегеніміз – жүйедегі теңсіздіктердің әрқайсысын тура теңсіздікке айналдыратын айнымалының мәндері.

 

Бір айнымалысы бар сызықтық теңсіздіктердің шешімдерін табу үшін:

1. Жүйедегі теңсіздіктердің әрқайсысының шешімдерін табу керек;

2. Табылған шешімдердің координатасын түзуде кескіндеу керек;

3. Координаталық түзуден жүйедегі теңсіздіктердің ортақ шешімдерін табу керек.

Жауабы: –4 < х < 0 немесе (–4; 0)

Натурал көрсеткішті дәреже ұғымы

Бірнеше тең көбейткіштердің көбейтіндісін табу амалын дєрежеге шығару деп атайды. Мысалы: 5•5•5•5=5⁴

 

1-ден үлкен а санының натурал көрсеткішті п дәрежесі деп әрбірі а- ға тең п көбейткіштердің көбейтіндісіне тең аⁿ өрнегін айтады. а дәреженің негізі, ал n дәреженің көрсеткіші деп аталады. Мысалы: (-3)¹=-3, (-3)²=(-3)(-3)=9, (-3)³=(-3)(-3)(-3)=-27, т.с.с. яғни: (-3)²ⁿ⁺¹<0, (-3)²ⁿ>0.

 

Көбейтудің қасиеттерінен:

1. Нөлдің кез келген натурал дәрежесі нөлге тең;

2. Оң санның кез келген дәрежесі оң сан.

Теріс санның тақ дәрежесі теріс сан, ал жұп дәрежесі оң сан.

Дәрежелерді көбейту және бөлу

Егер a кез келген сан, m және n натурал сандар болса, онда яғни, бірдей негіздегі дәрежелерді көбейткенде негізін сол қалпында қалдырып, дәреже көрсеткіштерін қосу керек.

Егер кез келген сан, m мен n натурал сандар болса, онда яғни, бірдей негіздегі дәрежелерді бөлгенде негізін сол қалпында қалдырып, бөлінгіштің дәрежесінен бөлгіштің дәрежесін шегеру керек.

Көбейтіндіні, бөлшекті және дәрежені дәрежеге шығару

Көбейтіндіні дәрежеге шығарғанда көбейткіштерді сол дәрежеге шығарып көбейтеді, яғни

 

Бөлшекті дәрежеге шығару үшін:

1. Бөлшектің алымын да, бөлімін де сол дәрежеге шығару керек;

2. Шыққан нәтижелерді бөлу керек.

 

Дәрежені дәрежеге шығарғанда негізінің өзін қалдырып, дәреже көрсеткіштерін көбейту керек.

Бүтін теріс көрсеткішті дәреженің ұғымы

Нөлге тең емес кез келген а санының (-n) дәрежесі деп а санының n-ші дәрежесіне кері санды айтады, яғни

 

Нөлдің теріс дәрежесінің мағынасы болмайды.

 

Мысалы: мұның мәні табылмайды.

Бүтін көрсеткішті дәреженің қасиеттері

Бүтін көрсеткішті дәреженің қасиеттері: кез келген және сандары мен кез келген бүтін n және m сандары үшін мына теңдіктер орындалады:

Санның стандарт түрі

Өте үлкен мәнді немесе өте кіші мәнді сандарды түрінде, (мұндағы ) жазуға болады. Санның осы түрде жазылуы стандарт түрі деп аталады.

 

Мысалы: күн диаметрі: 1 390 000 000м = 1,39 • 10⁹м,

Су молекуласы: 0,00000003см = 3 • 10 ^-8см.

Бірмүше және оның стандарт түрі

Сандардан, айнымалылардан және олардың дәрежелерінен көбейту амалы арқылы құрастырылған өрнекті бірмүше деп атайды.

 

Бірінші орында сан көбейткіш, ал оған жалғастырылған айнымалылар мен олардың дәрежелері жазылған бірмүшенің түрін стандарт түрі деп атайды.

 

Бірмүшенің алдындағы санды бірмүшенің коэффициенті деп атайды.

 

Бірмүше құрамындағы айнымалылардың дәрежелерінің қосындысын бірмүшенің дәрежесі деп атайды.

 

Мысалы: бірмүшесінің дәрежесі 2 + 1 + 3 = 6.

Бірмүшелерді көбейту. Бірмүшелерді дәрежеге шығару

Бірмүшелерді көбейткенде коэффициенттерін көбейтіп коэффициент етіп жазып, бірдей айнымалылардың дәрежелерін көбейтіп, сол айнымалалардың дєрежелерімен берілген бірмүшеге келтіреміз.

 

Бірмүшені дәрежеге шығарғанда әрбір көбейткішті осы дәрежеге шығарып, нәтижелерін көбейтеміз.

Көпмүше және оның стандарт түрі

Бірмүшеліктердің қосындысы көпмүше деп аталады. Ал оның құрамындағы бірмүшелер мүшелері деп аталады.

 

Мысалы: мұндағы мүшелері. Көпмүшедегі бірдей немесе коэффициенттері ғана өзгеше мүшелері ұқсас мүшелер деп аталады.

 

Көпмүшедегі ұқсас мүшелерді біріктіру теңбе-тең түрлендіру болады.

 

Көпмүшенің дәрежесі деп оның құрамындағы бірмүшелер дәрежесінің ең үлкенін айтады.

 

Егер көпмүшенің құрамында ұқсас мүшелер жоқ болса, онда оны стандарт түрдегі көпмүше дейді.

Көпмүшелерді қосу және азайту

Көпмүшелерді қосу үшін жақшаларды ашып ұқсас мүшелерін біріктіреміз.

 

Көпмүшелерді азайту үшін жақшаларды ашып ұқсас мүшелерді біріктіреміз.

 

Көпмүшелерді қосу және азайту кезінде жақша ашу ережесін қатаң сақтау керек:

1. Егер жақшаның алдында «+» таңбасы болса, онда көпмүше мүшелерін өз таңбаларымен жақшасыз жазамыз;

2. Егер жақшаның алдында « » таңбасы болса, онда көпмүше мүшелерін қарама-қарсы таңбаларымен жақшасыз жазамыз;

Бірмүше мен көпмүшенің көбейтіндісі. Бірмүшені көпмүшеге көбейту

Бірмүшені көпмүшеге көбейту үшін бірмүшені көпмүшенің әрбір мүшесіне көбейтіп, шыққан көбейтінділерді қосады.

 

Ортақ көбейткішті жақша сыртына шығару

Көпмүшені екі немесе бірнеше көпмүшенің көбейтіндісі түріне келтіруді көпмүшені көбейткіштерге жіктеу деп атайды.

 

Көпмүшені көбейткіштерге жіктеудің бір тәсілі ортақ көбейткішті жақша сыртына шығару деп атайды.

 

Көпмүшені көпмүшеге көбейту және бөлу

Көпмүшені көпмүшеге көбейту үшін бірінші көпмүшенің әрбір мүшесін екінші көпмүшенің әрбір мүшесіне көбейтіп, шыққан көбейтіндіні қосу керек.

Мысалы:

Көпмүшені топтау тәсілімен көбейткіштерге жіктеу

Көпмүшені топтау тәсілімен көюейткіштерге жіктеу үшін:

1. Көпмүшенің ортақ көбейткіштері бар мүшелерін топтау керек;

2. Әрбір топтағы ортақ көбейткішті жақша сыртына шығару керек;

3. Әр топтағы жақша ішіндегі көпмүшелер бірдей және ортақ көбейткіш болады

4. Осы көпмүшені ортақ көбейткіш ретінде жақша сыртына шығарамыз. Көпмүше екі көпмүшенің көбейтіндісіне келеді.

y = x^2, y = x^3 функциялары және олардың графиктері

y = x² функциясының графигі координаталар басы арқылы өтетін парабола деп аталатын қисық сызық болады және абсцисса осьінен жоғары орналасады, яғни тармағы жоғары қарайды. Тармақтары І, ІІ ширекте болады.

 

y = x³ функциясының графигі координаталар басына қатысты симметриялы болатын кубтық парабола деп аталатын қисық сызық болады. Оның графиктері І, ІІІ ширекте орналасады.

y = ax^2 және y = ax^3 функцияларының графиктері

y = ax² функциясының графигі төбесі координаталар басында жатқан парабола болады.

1. a > 1 болса, онда у = x² функциясының графигін 0у осьіне параллель бағытта а есе «созу» арқылы шығады;

2. 0 < a < 1 болса, онда у = x² функциясының графигін 0х осьіне қарай а есе «сығу» арқылы шығады;

3. a < 0 болса, онда ол y = ax² функциясының графигіне Ох осьіне қарағанда симметриялы болады.

y = ax³ функциясы графигі координаталар басы арқылы өтетін кубтық парабола болады.

1. a > 1 болса, онда у = x³ функциясының графигін Оу осьіне параллель бағытта а есе «созу» арқылы шығды;

2. 0 < a < 1 болса, онда у = x³ функциясының графигін Ох осьіне қарай а есе «сығу» арқылы шығады;

3. a < 0 болса, онда ол у = ax³ функциясының графигіне Оу осьіне қарағанда симметриялы болады.

Екі өрнектің қосындысының квадраты

Екі өрнектің қосындысының квадраты бірінші өрнектің квадратына, плюс екі еселенген бірінші және екінші өрнектердің көбейтіндісіне, плюс екінші өрнектің квадратына тең.

яғни: (a + b)² = a² + 2ab + b².

Мысалы: (2x + 3y)² = (2x)² + 2•(2x) • (3y) + (3y)² = 4x² + 12xy + 9y²

Екі өрнектің айырмасының квадраты

Екі өрнектің айырмасының квадраты бірінші өрнектің квадратына, минус екі еселенген бірінші және екінші өрнектердің көбейтіндісіне, плюс екінші өрнектің квадратына тең.

яғни: (a – b)² = a² – 2ab + b²

Мысалы: (3m – 5x)² = (3m)² – 2 •(3m) • (5x) + (5x)² = 9m² – 30mx + 25x²

 

 

Екі өрнектің айырмасы мен қосындысының көбейтіндісі

Екі өрнектің айырмасының олардың қосындысына көбейтіндісі осы өрнектердің квадраттарының айырмасына тең.

яғни: (a – b) • (a + b) = a² – b²

Мысалы: (8a + 9b) • (9b – 8a) = (9b – 8a) • (9b + 8a) = (9b)² – (8a)² = 81b² – 64a²

Екі өрнектің квадраттарының айырмасын көбейткіштерге жіктеу

Екі өрнектің квадраттарының айырмасы осы өрнектердің айырмасы мен қосындысының көбейтіндісіне тең.

яғни: a² – b² = (a – b) • (a + b)

 

Мысалы: 9a² – 25b² = (3a)² – (5b)² = (3a – 5b) • (3a + 5b)

Екі өрнектің кубтарының қосындысын көбейткіштерге жіктеу

Екі өрнектің кубтарының қосындысы осы өрнектердің қосындысын олардың айырмасының толымсыз квадратына көбейткенге тең.

яғни: a³ + b³ = (a + b) • (a^{2 –} ab + b²)

Мысалы: m³n³ + 8 = (mn)³ + 2³ = (mn + 2) • (m²n^{2 –} 2mn + 4)

Екі өрнектің кубтарының айырмасын көбейткіштерге жіктеу

Екі өрнектің кубтарының айырмасы осы өрнектердің айырмасын олардың қосындысының толымсыз квадратына көбейткенге тең.

яғни: a³ – b³ = (a – b) •(a² + ab + b²)

Мысалы: 27a³ – 64b³ = (3a)³ – (8b)³ = (3a – 8b) •(9a² + 24ab + 64b²)

Екі өрнектің қосындысының кубы

Екі өрнектің қосындысының кубы бірінші өрнектің кубына, плюс бірінші өрнектің квадраты мен екінші өрнектің үш еселенген көбейтіндісіне, плюс бірінші өрнек пен екінші өрнектің квадратының үш еселенген көбейтіндісіне, плюс екінші өрнектің кубына тең.

яғни: (a + b)³ = a³ + 3a²b + 3ab² + b³

 

Мысалы: (a + 2b)³ = a³ + 3a² • 2b + 3 • a •(2b)² + (2b)³ = a³ + 6a²b + 12ab² + 8b³

Екі өрнектің айырмасының кубы

Екі өрнектің айырмасының кубы – бірінші өрнектің кубына, минус бірінші өрнектің квадраты мен екінші өрнектің үш еселенген көбейтіндісіне, плюс бірінші өрнек пен екінші өрнектің үш еселенген квадратының көбейтіндісіне, минус екінші өрнектің кубына тең.

Яғни: (a – b)³ = a³ – 3a²b + 3ab² – b³

 

Мысалы: (x – 3y)² = x³ – 3 • x² • 3y + 3 • x •(3y)² – (3y)³ = x³ – 9x²y + 27xy² – 27y³

Бүтін өрнекті көпмүшеге түрлендіру

Қосу, азайту, көбейту, дәрежеге шығару және нөлге тең емес санға бөлу амалдарының көмегімен, сандар мен айнымалылардан құралған өрнекті бүтін өрнектер дейміз.

Бүтін өрнектерді көпмүшеге түрлендіру үшін сол өрнектердегі амалдарды орындап, шыққан өрнекті ықшамдау керек.

 

Мысалы: x • (1 – 2x)² – (x² – 2) • (2 – x) + 4x³• (3x – 1) = x• (1 – 4x + 4x²) – (2x² – x³ – 4 + 2x) + (12x⁴ – 4x³) = x – 4x² + 4x³ – 2x² + x³ + 4 – 2x + 12x⁴ – 4x³ = 12x⁴ + x³ – 6x² – x + 4.

Көпмүшені көбейткіштерге жіктеудің әр түрлі тәсілдерін қолдану

Көпмүшені көбейткіштерге жіктеу үшін ортақ көбейткішті жақша сыртына шығару тәсілін, топтау тәсілін, қысқаша көбейту формулаларын қолдану керек.

 

Мысалы: m³ – m²n – mn² + n³ көпмүшесін көбейткішке жіктеу керек:

 

1) топтау тәсілін қолдансақ: (m³ – m²n) – (mn² – n³).

2) ортақ көбейткіштерді жақша сыртына шығарсақ: m²(m – n) – n²(m – n) = (m – n)•(m² – n²)

3) екінші жақшаға қысқaша көбейту формулаларын (2.2) қолдансақ (m – n)•(m – n)•(m + n) яғни: m³ – m²n – mn²+ n³=(m – n)•(m – n)•(m + n) жіктеледі.

 

Рационал өрнектерді түрлендіру. Рационал өрнектер

Құрамында айнымалысы бөлімінде кездесетін бөлшектерді бөлшек өрнектер деп атайды. Ал жалпы бүтін өрнектермен бөлшек өрнектерді рационал өрнектер деп атайды.

 

Өрнектің мағынасы бар болатындай оның құрамындағы айнымалылардың барлық мәндері жиынын осы өрнектің мүмкін мәндер жиыны (М.М.Ж) деп атайды.

 

a/b түріндегі өрнекті рационал бөлшек деп атайды.

Рационал бөлшектерді қысқарту

Натурал a,b және с сандары үшін теңдігі орындалатыны белгілі. Бұл теңдік рационал бөлшектер үшін де орындалады, яғни a,b және с рационал өрнектер үшін: теңбе теңдігі орындалады, мұндағы: Бұл теңбе – теңдіктер рационал бөлшектердің негізгі қасиеті деп аталады. Осы қасиет бойынша өрнегімен ауыстыруға болады. Осы орындауды, яғни теңбе – теңдігін бөлшегін с көбейткішке қысқарту дейміз.

 

Егер бөлшектің алымының ( немесе бөлімінің) таңбасын өзгертсек, онда бөлшектің де таңбасы өзгереді, яғни

Бөлімдері бірдей бөлшектердің қосындысы мен айырмасы

Бөлімдері бірдей рационал бөлшектерді қосу үшін, олардың алымдарын қосып, бөлімдерін өзгеріссіз қалдыру керек.

 

Бөлімдері бірдей рационал бөлшектерді азайту үшін азайғыш бөлшектің алымынан азайтқыш бөлшектің алымын азайтып, бөлімін өзгеріссіз қалдыру керек.

Бөлімдері әр түрлі бөлшектерді қосу және азайту

Бөлімдері әр түрлі рационал бөлшектерді қосу үшін:

 

1) ортақ бөлімге келтіру керек,

2) бөлімдері бірдей бөлшектерді қосуды орындау керек.

 

 

Бөлімдері әр түрлі рационал бөлшектерді азайту үшін:

 

1) ортақ бөлімге келтіру керек,

2) бөлімдері бірдей бөлшектерді азайтуды орындау керек.

Рационал өрнектерді көбейту және бөлу. Бөлшектерді көбейту

Рационал бөлшектерді көбейту үшін, алымдарын көбейтіп алым етіп жазып, бөлімдерін көбейтіп бөлім етіп жазу керек.

Рационал өрнектерді көбейту және бөлу. Бөлшектерді бөлу

Рационал бөлшектерді бөлу үшін, бөлінгіш бөлшекті бөлгіш бөлшектің кері бөлшегіне көбейту керек.

Рационал өрнектерді теңбе-тең түрлендіру

Рационал өрнектерді теңбе тең түрлендіру бөлшектерді қосу, азайту, көбейту және бөлу амалдары арқылы орындалады.

y= k/x функциясы және оның графигі

y = k/x функциясын кері пропоционалдық деп атайды. Мұндағы х – тәуелсіз айнымалы, у – тәуелді айнымалы, ал к – кері пропоционалдықтың коэфициенті деп аталады. x≠0 үшін k/x өрнегінің мағнасы бар. Сондықтан анықталу облысы 0 – ден басқа сандар. k > 0 болғанда, y = k/x функциясының графигі I, III ширекте ораналасқан гипербола деп аталатын қисық сызық болады. k < 0 болғанда, y = k/x функциясының графигі II, IV ширекте ораналасқан гипербола деп аталатын қисық сызық болады.

 

k > 0 болса, функция анықталу облысында кемімелі, ал k < 0 болса, функция анықталу облысында өспелі болады.

Кездейсоқ оқиға ұғымы

Тиынды лақтырғанда ол елтаңба жағымен, не тиын жағымен түсуі мүмкін. Асықты лақтырғанда ол алшы,тәйке, шік, бүк болып түсуі мүмкін. Ойын сүйегін (әр жағында сандар жазылған кубик ) лақтырғанда түрлі ұпайдың бірі түсуі мүмкін т.с.с.

 

Міне осындай сынақтар (тәжірибелер) нәтижерелін оқиға деп атаймыз.

 

Ал осы сынақ нәтижесінде оқиғаның орындалуы да, орындалмауы да мүмкін болса, онда бұл оқиғаны кездейсоқ оқиға деп атаймыз.

 

Мысалы: тиынды лақтырғанда «елтаңба» түсуі, асықта лақтырғанда «алшы» түсуі, ойын сүйегін тастағанда «бес» ұпайдың түсуі – кездейсоқ оқиғалар.

Кездейсоқ оқиға жиілігі

Тиынды көп рет тастағанда оның «елтаңба» жағымен түсуін шамамен 50% – деп болжаймыз немесе 0,5 – ке тең. Бұл «елтаңба» оқиғаның түсу жиілігі деп аталады, яғни сынақты n рет жүргізу нәтижесінде бізге қажетті А оқиғасы m рет орындалды делік. Онда m/n саны A оқиғасының сынақты n рет өткізгендегі орындалу жиілігі деп аталады. Мысалы: ойын сүйегін 10 рет лақтырсақ 3 рет «бес» ұпай түсті. Ендеше осы сынақтағы «бес» ұпайдың түсу жиілігі 3/10 = 0,3 – ке тең.

Оқиғаның орындалу ықтималдығын оның жиілігі арқылы бағалау

Қандай бір сынақ нәтижесінде мүмкіндігі бірдей санаулы элементар оқиғалар орындалатын болса, онда А оқиғасының ықтималдылығы P(A) = m/n формуласымен анықталады. Мұндағы m – A оқиғасының қолайлы оқиғалар саны, n – A оқиғаның барлық мүмкін оқиғалар саны. Мысалы: Ойын сүйегін бір рет тастағанда «3» ұпайының түсу ықтималдығын есептейік. Ойын сүйегінің барлық мүмкін түсетін жағдайы алты, олар – 1, 2, 3, 4, 5, 6, яғни n = 6. Ал бізге қолайлы болып тұрған «3», яғни m = 1, ендеше «3» ұпайдың түсу ықтималдығы P(A) = 1/6 – ге тең.

Абсолюттік қателік

Жуық мән мен дәл мәннің айырмасының модулін жуық мәннің абсолют қателігі дейді.

Мысалы: 1/3 санын жүздік үлеске дейін дөңгелектесек мұндағы1/3 - дәл мәні, 0,33 - жуық мәні, абсолют қателігін тапсақ:

Салыстырмалы қателік

Абсолюттік қателіктің жуық мәннің модуліне қатынасы салыстырмалы қателік деп атайды.

 

Мысалы: 15,8 санын бірлікке дейін дөңгелектеп оның салыстырмалы қатесін есептесек, яғни

 

Салыстырмалы қателіктер процентпен де өрнектеледі. Ол үшін салыстырмалы қателіктің мәнін 100% көбейту керек.

Нақты сандар туралы түсінік

N- натурал сандар (1,2,3,4,...); Z - бүтін сандар (...-3,-2,-1,0,1,2,3,..); Q –рационал сандар (бүтін және бөлшек сандар); R – нақты сандар (рационал және иррационал сандар).

 

Рационал сандардың ішінде квадраты 2-ге тең сан жоқ. Кез-келген шексіз периодсыз ондық бөлшек иррационал сан деп аталады.Барлық рационал сан мен ирационал сандар нақты сандар жиынын құрайды.Нақты сандар жиынын сан түзуі деуге болады,яғни координаталық түзудегі әрбір нүктеге бір ғана нақты сан сәйкес келеді.Сан түзуінің геометриялық моделі – координаталық түзу.

Квадрат түбірдің анықтамасы,квадрат түбірдің жуық мәндері

3² = 9, 3-дәреженің негізі, 2 – дәреженің көрсеткіші,9 – дәреженің мәні.Берілген дәреженің мәні мен көрсеткіші бойынша дәреженің негізін табуды түбір шығару деп атайды.

 

- Теріс емес а санының квадрат түбірі деп квадраты а-ға тең в санын атайды. 64 санының квадрат түбірі 8 және -8,мұндағы 8 – арифметикалық квадрат түбір. Түбірдің оң мәнін арифметикалық квадрат түбір деп атайды. деп белгіленеді.

 

Саннан квадраттық түбір табудың қарапайым жолы:

мұндағы в саны а санына қарағанда неғұрлым кіші болса,түбірдің мәні де соғұрлым дәлірек болады. Мысалы:

Арифметикалық түбірдің қасиеттері

Арифметикалық түбірдің қасиеттері арифметикалық квадрат түбірі бар өрнектерді түрлендіру кезінде қолданылады.

1. дәреженің квадрат түбірі:

2. көбейтіндінің және бөлшектің квадрат түбірі:

Квадрат түбірі бар өрнектерді түрлендіру

Квадрат түбірі бар өрнектерді түрлендіргенде квадраттық түбірдің қасиеттерін қолданамыз.

 

1) көбейткішті түбір белгісінің алдына шығару.

өрнегін бірі толық квадрат болатын екі санның көбейтіндісіне жіктейміз:

2) көбейткішті түбір белгісінің астына алу. Түбір алдындағы көбейткіш түбір астына квадрат дәрежеде енеді.

 

3) Бөлшектің бөліміндегі иррационалдықтан арылу.

өрнегіндегі иррационалдықтан құтылу үшін формуласын еске түсіріп бөлімін де, алымын да өрнегіне көбейту керек.

 

Квадрат түбірі бар өрнектерді түрлендіргенде түріндегі құрама түбір өрнектері кездеседі. Түбір астындағы өрнекті екімүшенің квадратына келтіру үшін түрлендіру керек. Мысалы:

y = түбір асты х функциясы және оның қасиеттері мен графигі

Бұл функциясының анықталу аймағы х ≥ 0 аралығы, мәндерінің жиыны у ≥ 0 аралығы, сонда функциясының графигі координаталар басынан басталып I координаталық ширекте орналасқан сызық болады. Функция өспелі,яғни аргументтің үлкен мәніне функцияның үлкен мәні сәйкес келеді.

Квадрат теңдеу, квадрат теңдеудің түрлері

 

ax + ax² + c = 0, a ≠ 0 түріндегі теңдеулерді квадраттық теңдеу деп атайды. Мұндағы х-айнымалы шама, а,в,с нақты сандар, әрі а-екінші дәрежелі мүшенің коэффициенті, в-бірінші дәрежелі мүшенің коэффициенті, с-бос мүше. ax² + bx + c = 0 квадраттық теңдеуінде коэффициенттерінің бірі – в не с немесе в мен с- ның екеуі де нөлге тең болса,ондай теңдеулерді толымсыз квадраттық теңдеу деп атайды.

 

1) в = c = 0 болса, онда ax² = 0; шешуі: х = 0

2) c = 0, b ≠ 0 болса, онда ax² + bx = 0; шешуі : x (ax + b) = 0; х = 0; x= – b/a

3) с ≠ 0, b = 0 болса, онда ax² + c = 0; шешуі : x² =; егер –c/a ≥ 0 болғанда

 

 

Квадрат теңдеу түбірлерінің формулалары

Квадраттық теңдеу түбірінің формуласы: алдымен теңдеудің дискриминантын анықтап аламыз, яғни: D = b²– 4 ac.

1. Егер D > 0 болса, онда ax² + bx + c = 0, a ≠ 0 теңдеуінің ең болмағанда екі нақты түбірі:

болады.

1. Егер D = 0 болса, онда ax² + bx + c = 0, a ≠ 0 теңдеуінің өзара тең екі нақты сан түбірі

болады.

1. Егер D < 0 болса, онда ax² + bx + c = 0, a ≠ 0 теңдеуінің түбірі болмайды.