И удовлетворяли системе равенств

. (3.16)

Основную задачу линейного программирования можно представить в матричном виде

F = C X ® max , (3.17)

A X = B , (3.18)

X ³ 0, (3.19)

где C = [c₁ , …, c_j , …, c_n] – матрица-строка коэффициентов целевой функции;

– матрица коэффициентов системы ограничений;

– матрица-столбец коэффициентов правых частей ограничений, записанная в транспонированном виде;

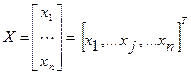– матрица-столбец переменных.

В частных задачах может потребоваться не максимизация, а минимизация целевой функции. В этом случае для сохранения алгоритма максимизации решается задача при целевой функции с обратным знаком, т. е. если F _min ® min, то в задаче берется F _max = – F_min .

Если в частной задаче в системе ограничений есть неравенства, то от них можно перейти к ограничениям-равенствам и, наоборот, от равенств можно перейти к неравенствам в случае исследования результатов решения.

Например, a₁₁ x₁ + … + a_1n x_n ³ b₁ (a₁₁ x₁ + … + a_1nx_n £ b₁ ) , или

a₁₁ x₁ + … + a_1n x_n – b₁ ³ 0.

Вводится новая переменная x_n+1, равная левой части неравенства

x_n+1 = a₁₁ x₁ + … + a_1n x_n – b₁ .

На эту новую переменную также накладывается условие неотрицательности x_n+1 ³ 0 . Перенеся новую переменную в левую часть неравенства, получим

a₁₁ x₁ + … + a_1n x_n – x_n+1 = b₁ или (a₁₁ x₁ + … + a_1n x_n + x_n+1 = b₁ ).

В целевую функцию дополнительные переменные входят с нулевыми коэффициентами:

F = c₁ x₁ + … + c_n x_n – 0 x_n+1 ® max.

В частой задаче требование неотрицательности может накладываться не на все переменные. Например, x_j не ограничено в знаке. В этом случае вводят замену

x_j = x_j^¢ – x_j^² , x_j^¢ ³ 0, x_j^² ³ 0.

Это увеличивает число переменных, но позволяет избежать трудностей при анализе решения двойственных задач.

Чтобы решить задачи линейного программирования надо ответить на три вопроса:

1) Имеет ли задача допустимые решения, т. е. совместна ли система ограничений?

2) Имеет ли целевая функция экстремум?

3) Каков этот экстремум, при каких значениях переменных достигается?

Набор чисел X = [x₁, …, x_j , …, x_n], удовлетворяющий условиям (3.14) и (3.16), называется допустимым решением.

Решение, при котором линейный функционал (3.15) достигает экстремума, называетсяоптимальным решением.

При анализе системы может оказаться:

1) условия (3.16) противоречивы, т. е. не существует набора чисел, удовлетворяющих этим условиям, в этом случае задача не имеет решения;

2) условия (3.16) непротиворечивы, но F не имеет экстремума, тогда задача тоже неразрешима.

Если 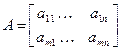– матрица системы, то 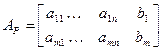– расширенная матрица системы, у которой добавлен столбец свободных членов.

Если в матрице произвольным образом выбрать k строк и k столбцов, то элементы, лежащие на их пересечении, образуют квадратную матрицу k – го порядка.

Определитель ее называется минором k – го порядкаматрицы А.

Рангом матрицы называется наивысший порядок миноров матрицы, отличных от нуля.

Теорема Кронекера-Капелли утверждает, что для того, чтобы система AX=B имела хотя бы одно решение, т. е. была совместна, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы.

Таким образом, тот общий ранг, который имеют матрица системы и расширенная матрица, составляет ранг системы и представляет собой число независимых уравнений в системе.

Если r–ранг системы, то r£ n(число неизвестных),r£ m (число уравнений).

Возьмем r = m и далее везде будем предполагать, что m – число независимых уравнений.

Рассматриваются обычно два случая, когда число уравнений равно или меньше числа переменных.

В первом случае, когда число уравнений равно числу переменных (m=n), система имеет единственное решение x₁ ,…, x_j ,…, x_n . В линейном программировании это редкий случай и практического значения не имеет.

Во втором случае число уравнений меньше числа переменных, т. е. m < n. Это наиболее распространенный вариант задач линейного программирования. В этом случае, если система ограничений совместна, она имеет бесконечное множество решений. При этом части переменных, число которых определяется разностью между m и n, можно придавать произвольные значения. Они называются свободными переменными. Остальные переменные можно выразить через свободные, и они называются базисными переменными.

Если хотя бы одна переменная отрицательная, то решение задачи недопустимо.