Задача потребительского выбора.
Считаясь с ограниченностью бюджета, потребитель выбирает набор товаров, приносящий ему наибольшее удовлетворение.
 ,
,  ,
, 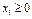 , где
, где  -вектор цен на набор продуктов
-вектор цен на набор продуктов 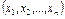 .
.
I – доход индивида, предназначенный для покупки набора 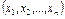 .
.
 - стоимость набора продуктов.
- стоимость набора продуктов.
Множество наборов, стоимость которых меньше I , образуют бюджетное множество.
Оптимальное решение задачи – точка локального рыночного равновесия - лежит на границе бюджетного множества.
В точке локального рыночного равновесия предельная норма замены i-го товара j-ым равна отношению рыночных цен на эти продукты.
тема 5. Метод искусственного базиса и основы теории двойственности.
Метод искусственного базиса. Каноническую ЗЛП заменяем на расширенную М задачу , вводя в каждое уравнение ограничение по одной «искусственной» переменной с коэффициентами 1 или (-1), в зависимости от знака свободного члена в этом уравнении.
«Искусственные» переменные объявляют базисными и включают в целевую функцию с коэффициентами М, если решается задача на минимум и (-М), если задача на максимум. М – число гораздо большее единицы.
В оценки векторов условий входят слагаемые, содержащие число М. Выписываем коэффициенты при М в отдельную строку оценок и при анализе результатов симплекс метода рассматриваем эту строку оценок.
Поэтапно выводим все «искусственные» переменные из базиса и из ЗЛП, затем поиск решения осущетвляем обычным симплекс – методом.
Свойства двойственных задач.
1.) Если целевая функция одной задачи в паре стремится к минимуму, то целевая функция другой задачи стремится к максимуму.
2) Коэффициенты при переменных в целевой функции одной задачи являются свободными членами системы ограничений в другой.
3)Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу.
Первая теорема двойственности:
Если одна из пары двойственных задач имеет оптимальное решение, то и двойственная к ней имеет оптимальное решение. Причём значения целевых функций этих задач на своих оптимальных решениях совпадают.
Оптимальное решение одной из задач можно найти из решения симплекс методом другой задачи, прибавив к оценкам разложений по базису оптимального решения векторов, входящих в начальный базис начального решения соответствующие коэффициенты целевой функции.
Если одна из пары двойственных задач не имеет решения ввиду неограниченности целевой функции, то другая не имеет решения ввиду несовместности системы ограничений.
Вторая теорема двойственности:
Допустимые решения  и
и  являются оптимальными решениями пары двойственных задач тогда и только тогда, когда
являются оптимальными решениями пары двойственных задач тогда и только тогда, когда 
 и
и 
