Тема 3. Геометрическое решение задач математического программирования.

Рассмотрим ЗМП с двумя неизвестными:

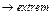- целевая функция - система ограничений

1) Строим ОДР задачи.

Областью решения каждого из неравенств 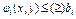будет часть плоскости, ограниченная линией . Очевидно, что решением системы неравенств будет пересечение всех их областей решений. 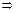ОДР задачи МП – общая часть областей решений всех неравенств системы ограничений.

Если ОДР – пустое множество, задача не имеет решения в силу несовместности системы ограничений.

Если ОДР – непустое множество, задача имеет одно или бесконечное множество решений.

2)Строимлинии уровняцелевой функции (линии, в которых значение функции постоянно).

=С –уравнения линий уровня.

Если Z – линейная функция, то её линии уровня – семейство прямых, перпендикулярных вектору градиенту этой функции.

Вектором градиентом функции называется вектор , координаты которого равны частным производным этой функции.

3) Двигаясь от одной линии уровня к другой в направлении вектора градиента (в задачах на максимум) или в противоположном направлении (в задачах на минимум), находим опорную кривую.

Опорная кривая _ такая линия уровня, которая имеет хотя бы одну общую точку с ОДР, и, при этом, не разделяет её на части.

4) Находим оптимальное решение задачи – общие точки ОДР и опорной кривой.

тема X. Модель поведения потребителя.

Пусть = 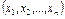- набор из n товаров потребления ( 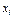- количество i-го товара, ).

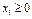Каждый потребитель определяет для себя ценность любого набора товаров, задавая тем самым функцию потребительского предпочтения, или функцию полезности товара. .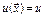

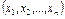Тогда предельная полезность i-го товара - .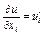

Свойства функции полезности:

1)Все её первые частные производные положительны. 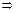возрастание потребления одного продукта при неизменном потреблении других приводит к росту потребительской оценки всего набора.

2) Закон Госсена. <0. 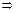предельная полезность любого товара уменьшается с ростом его потребления.

3) Смешанные частные производные второго порядка положительны. 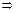предельная полезность любого товара увеличивается с ростом потребления другого.

Линии безразличия функции полезности - линии, соединяющие потребительские наборы, имеющие один и тот же уровень полезности для потребителя. Они не имеют общих точек, не пересекаются и выпуклы вниз.