Основные теоретические сведения

Оценка степени риска поражения людей и нанесения ущерба при авариях связана с задачей прогнозирования показателей надежности и остаточного ресурса функционирующей системы. Наиболее важным вопросом является установление допустимых сроков дальнейшей эксплуатации индивидуального объекта при конкретном значении риска аварии.

Одним из основных показателей надежности объекта является вероятность P(t) безотказной работы на некотором временном интервале (функция надежности). Функция Q(t)=1–P(t),дополняющая P(t) до единицы и характеризующая вероятность отказа, является функцией риска аварии – поражения людей и нанесения материального ущерба.

Прогнозирование аварийных ситуаций возможно на основе элементарной статистики и дискретного распределения Пуассона, часто применяемого к редким событиям и природным явлениям.

Функцией риска аварии из-за отказа нормального функционирования объекта называют вероятность отказа:

 

H(t) = 1 – P'(t), P'(t) = exp (–∫ λ (ξ) d ξ), λ(t) = – P'(t) / P(t), (5.1)

 

где Р(t) – вероятность безотказной работы (функция надежности); λ(t) – интенсивность отказов, равная вероятности того, что после безотказной работы до момента времени t авария произойдет в последующем малом отрезке времени.

Опыт показывает, что после небольшого начального периода эксплуатации (приработки) функция λ(t) длительный период достаточно стабильна, т. е. λ(t) = const. Влияние интенсивного старения за счет коррозионного износа, усталости и других факторов должно исключаться регламентированием допустимого срока службы.

Принимая для периода нормального (спокойного) функцио­нирования λ(t) = const, из (5.1) получают экспоненциальное распределение

 

P(t) = exp(–λτ), (5.2)

 

причем θ = 1/λ – математическое ожидание срока службы (ресурса) или средняя наработка на отказ. Функцию риска теперь можно записать в виде

 

H(t) = 1 – exp(– t/θ). (5.3)

 

При функции надежности в виде (5.2) частота отказов в системе однотипных объектов (поток случайных событий) со­ответствует дискретному распределению Пуассона

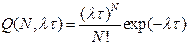, N = 0,1,2,… λτ > 0 . (5.4)

Согласно данной формуле, аварии на временном интервале τ (t, t + τ) произойдут N раз с вероятностью Q(N, λτ), а отсутствие аварийных ситуаций (отсутствие отказов) – с вероятностью

Q(0,λτ) = exp(– λτ).(5.5)

Вероятность того, что аварии произойдут n разпри n < N (т. е. менее N раз), определяется функцией распределения

Q₀(n<N)= 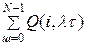=1 – φ(N,λτ) (5.6)

φ(N, λτ)= Q₀(n≥N)= .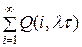

Вероятность 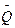возникновения хотя бы одной аварии пред­ставляет оценку риска аварий на объекте в период τ

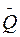= 1– Q(0, λτ) = 1 – exp(–λτ) . (5.7)

 

Для математического ожидания Ν, дисперсии D и стандарта σ (среднеквадратического отклонения) имеет место равенство N = D = σ²= λτ, т. е. имеется возможность экспериментальной проверки правдоподобия гипотезы о применимости закона Пуассона к конкретному виду аварии по факту хотя бы приблизительного соблюдения равенства N = D.

Таким образом, прогнозирование аварийных ситуаций воз­можно на основе статистики. Такого рода данные представляют интерес при принятии решений о мерах по снижению степени риска аварий на объектах.

 

Литература: [3], [6], [7], [9].