Функция распределения Максвелла-Больцмана. Барометрическая формула.

Билет

1) Кинематика материальной точки. Система отсчета, радиус – вектор, перемещение, путь, скорость, ускорение

Кинематика материальной точки - раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение.
Система отсчета– Совокупность неподвижных друг относительно друга тел, по отношению к которым рассматривается движение и отсчитывающих время часов.
Радиус-вектор - Вектор, задающий положения точки в пространстве (например, гильбертовом или векторном) относительно некоторой заранее фиксированной точки
Перемещение - изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта.
Путь - это длина траектории движения тела.
Перемещение- это отрезок, соединяющий начальное и конечное положение тела.
Скорость – Быстрота перемещения тела и направление в котором движется частица в каждый момент времени.
Ускорение – векторная величина, характеризующая быстроту изменения скорости движущегося тела по величине и направлению.

2) Волны. Общая характеристика волновых процессов. Уравнение плоской волны. Фазовая и групповая скорости волн

Волны– Бывают два вида волн: Продольные и поперечные. Если колебательный процесс перпендикулярен направлению распространению волны – поперечные. Если колебание вдоль – продольные.

Продольные волны - колебания среды происходят вдоль направления распространения волн, при этом возникают области сжатия и разрежения среды.
Поперечные волны - колебания среды происходят перпендикулярно направлению их распространения, при этом происходит сдвиг слоев среды.

Уравнение плоской волны -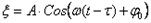
Фазовая скорость волны - скорость перемещения точки, обладающей постоянной фазой колебательного движения, в пространстве
вдоль заданного направления.
Групповая скорость - определяет скорость и направление переноса энергии волнами

Билет

1) Прямолинейное и криволинейное движение. Тангенциальное и нормальное ускорения

Прямолинейное движение — механическое движение, при котором вектор перемещения ∆r не меняется по направлению, его модуль равен длине пути, пройденного телом
Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движении изменяется по величине и по направлению.
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Нормальное ускорение - векторная величина, характеризующая быстроту изменения скорости движущегося тела по величине и направлению.

2) Принципы относительности Галилея, преобразования Галилея.

Принцип относительности Галилея - гласит, что все физические процессы в инерциальных системах отсчёта протекают одинаково, независимо от того, неподвижна ли система или она находится в состоянии равномерного и прямолинейного движения.
Преобразования Галилея - Преобразования Галилея опираются на принцип относительности Галилея, который подразумевает одинаковость времени во всех системах отсчета («абсолютное время»)

Билет

1) Кинематика вращательного движения

Если в процессе движения абсолютно твердого тела его точки А и В остаются неподвижными, то и любая точка С тела, находящаяся на прямой АВ, также должна оставаться неподвижной. В противном случае расстояния АС и ВС должны были бы изменяться, что противоречило бы предположению об абсолютной твердости тела. Поэтому движение твердого тела, при котором две его точки Аи В остаются неподвижными, называют вращением тела вокруг неподвижной оси, а неподвижную прямую АВ называют осью вращения.

Рассмотрим произвольную точку М тела, не лежащую на оси вращения АВ. При вращении твердого тела расстояния М А и МВ и расстояние ρ точки М до оси вращения должны оставаться неизменными. Таким образом, все точки тела, вращающегося вокруг неподвижной оси, описывают окружности, центры которых лежат на оси вращения, а плоскости перпендикулярны этой оси. Движение абсолютно твердого тела, закрепленного в одной неподвижной точке, называют вращением тела вокруг неподвижной точки - центра вращения. Такое движение абсолютно твердого тела в каждый момент времени можно рассматривать как вращение вокруг некоторой оси, проходящей через центр вращения и называемой мгновенной осью вращения тела. Положение мгновенной оси относительно неподвижной системы отсчета и самого тела с течением времени может изменяться.

2) Опыт Майкельсона. Постулаты СТО. Преобразования Лоренца, следствия из преобразований Лоренца

Опыт Майкельсона — физический опыт, поставленный Альбертом Майкельсоном на своём интерферометре в 1881 году, с целью измерения зависимости скорости света от движения Земли относительно эфира. Под эфиром тогда понималась среда, аналогичная объёмно распределённой материи, в которой распространяется свет подобно звуковым колебаниям. Результат эксперимента по мнению Майкельсона был отрицательный — смещение полос не совпадают по фазе с теоретическими, но колебания этих смещений только немного меньше теоретических. Существование эфира опровергнуто.
1) все явления природы протекают абсолютно одинаково во всех инерциальных системах отсчета.
2) С – величина постоянная и не зависит от скорости движения инсточника и приемника света
3) с позиции 2 постулата легко доказать что события одновременны в одной системме отсчета являются неодновременными в другой системе отсчета

Билет

1) Понятие массы, силы, импульса.

Импульс – Произведение массы тела на его скорость.
Масса – это свойство тела, характеризующее его инертность. При одинаковом воздействии со стороны окружающих тел одно тело может быстро изменять свою скорость, а другое в тех же условиях – значительно медленнее
Сила – это количественная мера взаимодействия тел. Сила является причиной изменения скорости тела. В механике Ньютона силы могут иметь различную физическую причину: сила трения, сила тяжести, упругая сила и т. д. Сила является векторной величиной.

2) Сложение скоростей. Пространственно-временной интервал

При рассмотрении сложного движения (то есть когда точка или тело движется в одной системе отсчёта, а она движется относительно другой) возникает вопрос о связи скоростей в 2 системах отсчёта.
В классической механике абсолютная скорость точки равна векторной сумме её относительной и переносной скоростей:
Данное равенство представляет собой содержание утверждения теоремы о сложении скоростей.
Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости (относительно неподвижной системы) той точки подвижной системы отсчёта, в которой в данный момент времени находится тело.

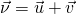
Билет

1) Законы Ньютона. Инерциальные и неинерциальные системы отсчета. Силы инерции.

Законы Ньютона - три закона, лежащие в основе классической механики и позволяющие записать уравнения движения для любой механической системы, если известны силовые взаимодействия для составляющих её тел.

1) Если на тело не действует внешняя сила, то тело находится в состоянии покоя или равномерного прямолинейного движения.
2) F=ma Ускорение тела прямо пропорционально равнодействующей силе и обратно пропорционально его массе
3) Сила действия равна силе противодействия F1 = - F2

Инерциальная система отсчета (ИСО) - система отсчета, в которой справедлив закон инерции: все свободные тела (то есть такие, на которые не действуют внешние силы или действие этих сил компенсируется) движутся в них прямолинейно и равномерно или покоятся в них. Только в этих системах выполняются законы Ньютона.

Неинерциальная система отсчета - произвольная система отсчета, не являющаяся инерциальной. Всякая система отсчета, движущаяся с ускорением относительно инерциальной, является неинерциальной.

Сила инерции, векторная величина, численно равная произведению массы т материальной точки на ее ускорение w и направленная противоположно ускорению. При криволинейном движении С. и. можно разложить на касательную, или тангенциальную составляющую J_t направленную противоположно касательному ускорению w_t, и на нормальную, или центробежную составляющуюJ_n, направленную вдоль главной нормали к траектории от центра кривизны; численно J_t = nw_t, J_n =mv²/r, где v — скорость точки, r — радиус кривизны траектории. При изучении движения по отношению к инерциальной системе отсчёта С. и. вводят для того, чтобы иметь формальную возможность составлять уравнения динамики в форме более простых уравнений

2) Импульс. Закон движения в релятивистской динамике. Энергия, взаимосвязи массы и энергии. Законы сохранения в СТО.

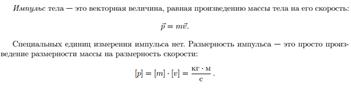
Релятивистский закон сложения скоростей тела и скорости движущейся системы в одном

где u ' – скорость движения тела в движущейся системе отсчета; v – скорость движущейся системы K ' относительно неподвижной системы K;
u – скорость тела относительно неподвижной системы отсчета K (рис. 1).

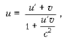
Релятивистское замедление времени Время t₀, отсчитываемое по часам, покоящимся относительно данного тела, называется собственным временем. Оно всегда меньше времени, измеренного по движущимся часам: t₀ < t.

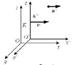
Релятивистское сокращение длины Поперечные размеры движущегося стержня не изменяются. Линейный размер стержня l₀ в той системе отсчета, где он покоится, называется собственной длиной. Эта длина максимальна: l₀ > l.

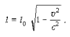
Импульс движущегося тела (релятивистский импульс):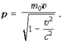

Полная энергия тела или системы тел: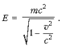

6 Билет
1) Закон сохранения импульса. Центр масс. Движение центра масс.

Закон сохранения импульса - В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называется законом сохранения
импульса. Он является следствием из второго и третьего законов Ньютона.

P – Импульс системы; F - равнодействующая всех сил, действующих на частицы системы

Центр масс - геометрическая точка, характеризующая движение тела или системы частиц как целого.
Теорема о движении центре масс (центра инерции) системы - общая проблема динамики. что ускорение центра масс механической системы не зависит от внутренних сил, действующих на тела системы, и связывает это ускорение с внешними силами, действующими на систему. Центр масс движется так, как двигалась бы материальная точка, масса которой равна массе системы, под действием силы, равной сумме всех внешних сил, действующих на систему. ma=(сумма F)

2) Термодинамические параметры. Идеальный и реальный газы. Уравнение состояния идеального и реального газов.

Термодинамическими величинами называют физические величины, применяемые при описании состояний и процессов в термодинамических системах.

1) Температура - физическая величина, примерно характеризующая приходящуюся на одну степень свободы среднюю кинетическую энергию частиц макроскопической системы, находящейся в состоянии термодинамического равновесия.
2) Давление - это нормальная к поверхности (перпендикулярная) сила, действующая на единицу площади: р = F/A.
3) Объём - количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.
4) Энтропия– степень разупорядоченности системы. Самопроизвольно в природе все процессы идут в одну сторону: в сторону роста энтропии. Св-ва (или растет или не меняется; это функция состояния; энтропия системы тел складывается из энтропии тел, входящих в систему; внутренняя энтропия = свободная энергия + связанная энергия)

Идеальный газ – газ в котором можно пренебречь взаимной потенциальной энергией молекул и собственным объемом молекул.
В реальных газах плотность настолько велика, что нельзя пренебречь взаимной потенциальной энергией. Собственный объем молекул тоже играет роль. В качестве эксперимента можно сделать следующее: берем баллон помещаем туда идеальный газ, очень медленно сжимаем. При этом температура должна быть постоянной за счет теплообмена с окружающей средой.
Соотношение между давлением и объемом подчиняется закону Бойля-Мариота. Давление обратно пропорционально объему.
Если увеличить концентрацию, то взаимное притяжение увеличится. Потенциальной энергией нельзя пренебречь
(газ реальный 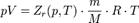). Между давлением и объемом нет обратно пропорциональной зависимости.

Билет

1)Момент инерции, момент силы и момент импульса. Теорема Штейнера

Моментом инерции системы относительно оси вращения называется физическая величина, равная сумме произведения масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси.
Если известен момент инерции тела относительно оси, проходящей через его центр масс, момент инерции относительно любой другой оси параллельной данной, определяется с помощью теоремы Штейнера: момент инерции тела І относительно параллельной оси вращения равен моменту инерции І_с относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями

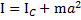
Моментом силы 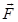относительно неподвижной точки O называется псевдовекторная величина равная векторному произведению радиус-вектора 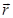, проведенному из точки O в точку приложения силы, на силу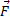

Модуль момента силы:

Моментом импульса твердого тела относительно неподвижной оси Z называется скалярная величина равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки O данной оси. Значение момента импульса не зависит от положения точки O на оси Z.

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц.

Момент ипульса - характеризует количество вращательного движения. Момент импульса материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:

L=r×p,
где r радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, p - импульс частицы.

2) Внутренняя энергия идеального и реального газов.

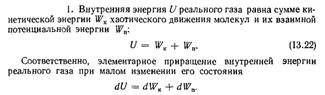
Исходя из определения идеального газа, в нем отсутствует потенциальная составляющая внутренней энергии (отсутствуют силы взаимодействия молекул, кроме ударного). Таким образом, внутренняя энергия идеального газа представляет собой только кинетическую энергию движения его молекул.

Билет

1) Основное уравнение динамики вращательного движения. Закон сохранения момента импульса.

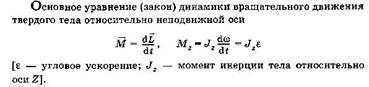
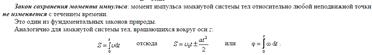
2) Степени свободы молекул. Теорема равнораспределения энергии по степеням свободы.

степеней свободы молекул - число независимых координат, которые необходимо задать, чтобы однозначно определить положение этого объекта относительно рассматриваемой системы отсчета.

а- одноатомной (3), б- двухатомной(5), в- трехатомной(6).

Среднюю кинетическую энергию движения молекулы идеального газа можно определить по формуле: 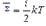iчисло независимых величин, определенных положением тела в пространстве.

У любого тела при поступательном движении три степени свободы. На каждую степень свободы статистической системы приходится одна и та же энергия, равная 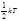. ΣƩ

В этом состоит суть теоремы о равнораспределении тепловой энергии по степеням свободы.

Для одноатомных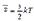

Для двухатомных – 2 степени свободы. Колебания степеней свободы совершаются при значительном росте температуры, т.к. ослабевают межатомные связи и усиливаются колебания внутри молекул.

Для самой большого увеличения температуры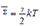

Билет

1) Работа постоянной и переменной силы. Кинетическая энергия тела, участвующего в поступательном и вращательном движениях.

Работа постоянной силы. Для характеристики эффективности силового воздействия на тело используется величина, называемая механической работой. Пусть под действием постоянной силы F частица произвольным образом переместилась из положения 1 в положение 2. Работой силы F на перемещении ∆r называется скалярная величина, определяемая следующим соотношением: Работа постоянной силы равняется скалярному произведению силы на перемещение.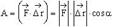

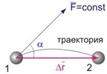
Единица измерения работы - Джоуль. 1 Дж = 1 Н·м.
Работа переменной силы

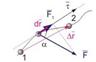
Работа переменной силы. В случае движения под действием переменной силы величина работы рассчитывается следующим образом. Всю траекторию мысленно разбивают на отдельные участки такой малой длины |dr|, что действующую на них силу можно считать постоянной (см. рис. 7.2). Проекция силы на направление вектора элементарного перемещения drпредставляет собой ее тангенциальную составляющую. Следовательно, элементарную работу на перемещении dr можно рассчитать с помощью соотношения.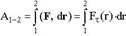

2) Первое начало термодинамики и его применения к изопроцессам. Адиабатический процесс

Изопроцессы - процессы, протекающие при неизменном значении одного из параметров.

Изотермический процесс (T = const, следовательно ΔU = 0).
По первому закону термодинамики: Q = A'.
Газ совершает работу A' за счет подводимого тепла Q (A'>0, Q>0).
Совершение работы внешними силами A (сжатие газа) требует отвода тепла Q от газа для сохранения его температуры (A>0, Q<0).

Изохорный процесс (V = const, следовательно A = 0).
По первому закону термодинамики: ΔU = Q.
Нагревание газа в закрытом сосуде приводит к увеличению его внутренней энергии U (температуры) (Q>0, ΔU>0).
Охлаждение газа в закрытом сосуде приводит к уменьшению его внутренней энергии U (температуры) (Q<0, ΔU<0).

Изобарный процесс (p = const).
По первому закону термодинамики: Q = ΔU + A'.
Подводимое к газу тепло Q частично идет на увеличение внутренней энергии U, а частично на совершение работы газом A' (Q>0, ΔU>0, A'>0).
Работа внешних сил A при изобарном сжатии газа требует отвода тепла Q от газа, одновременно уменьшается его внутренняя энергия U (Q<0, ΔU<0, A>0).

Адиабатный процесс - процесс, протекающий без теплообмена с окружающей средой (Q = 0).
По первому закону термодинамики: ΔU = A.
Вся работа внешних сил А идет только на увеличение внутренней энергии газа (A>0, ΔU>0).
Работа газа А' совершается только за счет потери внутренней энергии газа (A'>0, ΔU<0).

Билет

1) Потенциальная энергия. Потенциальная энергия сжатой пружины, тела в поле тяготения.

Потенциальная энергия — скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в поле консервативных сил. Зависит от положения материальных точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы^]. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином.

Единицей измерения энергии в Международной системе единиц (СИ) является джоуль.

Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения.

Потенциальная энергия тела 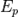в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

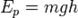
где 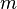— масса тела, 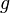— ускорение свободного падения, 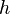— высота положения центра масс тела над произвольно выбранным нулевым уровнем.

2) Работа сил тяготения, связь силы и потенциальной энергии. Работа газа в изопроцессах.

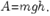Пространство, в котором действуют консервативные силы, называется потенциальным полем. Каждой точке потенциального поля соответствует некоторое значение силы F, действующей на тело, и некоторое значение потенциальной энергии U. Значит, между силой F и U должна быть связь , с другой стороны, dA = –dU, следовательно Fdr=-dU, отсюда: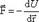

Проекции вектора силы на оси координат:

Вектор силы можно записать через проекции: 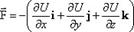, F = –grad U, где .

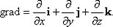В изохорном процессе (V = const) газ работы не совершает, A = 0.

В изобарном процессе (p = const) работа, совершаемая газом, выражается соотношением:

A = p (V₂ – V₁) = pΔV.

В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, ΔU = 0.

Работа газа в адиабатическом процессе выражается через температуры T₁ и T₂ начального и конечного состояний:

A = C_V (T₂ – T₁).

Билет

1) Закон сохранения энергии – фундаментальный закон природы.

Закон сохранения энергии — фундаментальный закон природы, заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии.

Формулировка закона сохранения и превращения энергии:

Во всех явлениях, происходящих в природе, энергия не возникает и не исчезает. Она только превращается из одного вида в другой, при этом ее значение сохраняется. E=mc²

2) Теплоемкость идеального газа

Теплоемкость– величина равная количеству тепла, которое нужно сообщить чтобы изменить температуру на 1 градус.

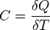
дж/кг*К

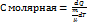дж/моль*К одного моля

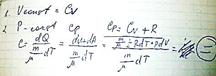
Из этого соотношения следует, что 1 моль идеального газа при увеличении температуры на 1 К расширяется и совершает работу равную R (A=R=8,31 Дж)

Ср= R(i/2 + 1) = R (i+2)/2

Билет

1) Свободные незатухающие гармонические колебания. Одномерный гармонический осциллятор.

Свободные незатухающие гармонические колебания -колебания, при которых полная механическая энергия системы не меняется. Гармонический процесс в том случае, когда величина, хар-ющая колебательный процесс изменяется по закону sin или cos. Одномерный гармонический осциллятор - атермальная точка массы m, совершающая прямолинейные гармонические колебания под действием упругой силы(F=-kx).

2) Приведенная теплота. Равенство и неравенство Клаузиуса. Энтропия. Статистический смысл энтропии.

Энтропия – степень разупорядоченности системы. Самопроизвольно в природе все процессы идут в одну сторону: в сторону роста энтропии.

Приведенное количество теплоты – отношение тепла полученного системой к температуре этой системы. Q* = (Q/T) – изотермический процесс

В замкнутом круговом цикле тождественно равно 0. Если процесс не изотермический, разбиваем процесс на очень малые временные участки и собираем количество тепла.

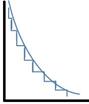
A =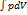

Энтропия – функция. Полный дифференциал которой равен приведенному значению тепла в изотермическом процессе. Степень разупорядоченности системы (энтропия) – любой замкнутой системы самопроизвольно растет. Процесс необратим. (∆S>0) если процесс обратимый внутри системы и окр.телах, то роста энтропии нет. (степень разупорядоченности не меняется) ∆S=0 S – const

∆S≥0 – второй вариант энтропии. Передача тепла от более нагретого тела к менее нагретому. Q≠∆V+A Q≠A – Кельвин-Планк Клаузиус. Если процесс обратимый – не меняется. Есл ине обратимый – всегда растет

1 энтропия или растет или не меняется

2 энтропия– функция состояния

3 энтропия системы тел складывается из этропии тел входящих в систему.

4 внутренняя энергия = свободная энергия + связанная энергия U = F + TS

Невозможен в природе процесс единственным результатом которого было бы совершение работы подведенному количеству тепла.

Невозможен в природе процесс единственным результатом которого было бы передача тепла от менее нагретого к более нагретому телу.

Билет

1) Энергия гармонических колебаний.

При гармонических колебаниях любых физических систем непрерывно и периодически происходит превращение кинетической энергии в потенциальную и обратно.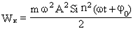

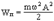
2) Формулировки второго начала термодинамики.

В природе все процессы самопроизвольно идут в сторону роста разупорядоченности. Все процессы необратимые.. энергия упорядочения движения переходит в энергию хаотического теплового движения. Назад процесс не пойдет.

Степень разупорядоченности системы (энтропия) – любой замкнутой системы самопроизвольно растет. Процесс необратим. (∆S>0) если процесс обратимый внутри системы и окр.телах, то роста энтропии нет. (степень разупорядоченности не меняется) ∆S=0 S – const

∆S≥0 – второй вариант энтропии. Передача тепла от более нагретого тела к менее нагретому. Q≠∆V+A Q≠A – Кельвин-Планк Клаузиус.

1) невозможен процесс, единственным результатом которого является передача энергии в форме теплоты от менее нагретого тела к более нагретому телу;
2) невозможен периодический процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу.

15 билет

1) Математический и физический маятники.

Маятник – тело. Колеблющееся по действием сил тяготения.

Математический маятник – система, состоящая из длинной нерастяжимой нитии материальной точки, подвешенной на ней.

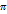
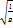
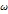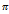T = 2 ₀=2 /Т

Если угол отклонения не больше 5-7 градусов. В противном случае g ≠ 9.8

Физический маятник – тело, которое может совершать колебания, относительно оси, не проходящей через центр тяжести этого тела. T = 2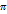

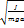
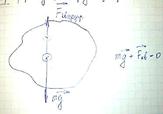
Положение безразличного равновесия – ось проходит через центр тяжести.

m-масса A – расстояние между осью и центром тяжести g – постоянная

l = I/ma - приведенная длина физического маятника. Длина математического маятника с равным периодом физических колебаний.

2) Вероятностное описание случайных событий. Функция распределения. Распределение молекул по кинетическим энергиям Максвелла. Расчет средних значений.

Непрерывная случайная величина Х называется распределенной по нормальному закону, если ее плотность распределения равна

где 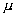совпадает с математическим ожиданием величины Х: 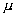=М(Х), параметр s совпадает со средним квадратическим отклонением величины Х: s =s(Х).

Функция распределения- функция распределения по уровням энергии тождеств. частиц с нулевым или целочисл. спином при условии, что взаимодействие частиц слабое и им можно пренебречь, т. е. ф-ция распределения идеального квантового газа, подчиняющегося Бозе - Эйнштейна статистике.

В случае статистич. равновесия ср. число 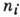таких частиц в состоянии с энергией e_i при темп-ре T выше вырождения температуры определяется Б--Э. р.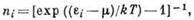

Закон Максвелла описывается некоторой функцией f(ν), которая называется функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, которые равны dν, то на каждый интервал скорости приходится число молекул dN(ν), имеющих скорость, которая заключена в этом интервале. Функция f(ν) задает относительное число молекул dN(ν)/N, скорости которых находятся в интервале от ν до ν+dν, т. е. 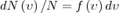откуда Применяя методы теории вероятностей, Максвелл получил функцию f(ν) — закон о распределения молекул идеального газа по скоростям:
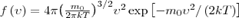(1)По определению среднее значение физической величины А равно: где Ai- значение физической величины в состоянии i, а () w Ei - вероятность реализации

состояния i.

Билет

1) Свободные затухающие колебания.

Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида в природе невозможен.

Свободными колебаниями называются колебания тел под действием внутренних сил, после того как система была выведена из положения равновесия.

Все реальные колебательные системы являются диссипативными. Энергия механических колебаний такой системы постепенно расходуется на работу против сил трения, поэтому свободные колебания всегда затухают - их амплитуда постепенно уменьшается. Во многих случаях, когда отсутствует сухое трение, в первом приближении можно считать, что при небольших скоростях движения силы, вызывающие затухание механических колебаниях, пропорциональны скорости. Эти силы, независимо от их происхождения, называют силами сопротивления.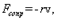

где r - коэффициент сопротивления, v - скорость движения. Запишем второй закон Ньютона для затухающих колебаний тела вдоль оси ОХ .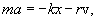

Затухающие колебания представляют собой непериодические колебания, так как в них не повторяется, например, максимальное значение амплитуды. Поэтому называть ω – циклической (повторяющейся, круговой) частотой можно лишь условно. По этой же причине и

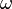T=2π/ =2π/( 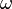^2-β^2)^1/2;здесь ^-это степень,а ^1/2-это корень(квадратный).

называется условным периодом затухающих колебаний.

2) Распределение молекул по потенциальным энергиям Больцмана.

PV = 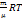- уравнение Менделеева-Клайперрона

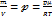
Исходя из уравнения Менделеева-Клайпейрона получаем зависимость плотности от параметрического состояния.

Чем больше h, тем меньше давление при постоянной температуре.

При постоянном давлении одновременно действует с одной стороны сила трения, а с другой стороны тепловое воздействие. Чем больше масса молекул, тем меньше этих молекул.

Билет

1) Вынужденные колебания. Явление резонанса.

Вынужденные колебания в отличие от свободных колебаний совершаются не самостоятельно, а под действием периодической внешней силы. Например, электрические колебания в антенне приемника не являются свободными, так как они происходят под воздействием приходящих радиоволн.

Резонанс – когда частота внешней вынужденной силы совпадает с частотой собственного колебания системы, тогда амплитуда резко возрастает.

Функция распределения Максвелла-Больцмана. Барометрическая формула.

Распределение вероятностей различных энергетических состояний идеальной термодинамической системы (идеальный газ атомов или молекул) в условиях термодинамического равновесия

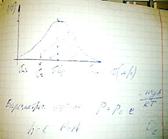
В показатели степени экспоненты находится отношение потенциальной энергии к энергии тплового движения. Надем связь между концентрацией молекул, мссой молекулы, высотой. На которой находятся молекулы над поверхностью земли и температурой.

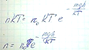
Чем больше температура, тем молекулы больше. Чем выше высота, тем меньше концентрация. Чем больше масса, тем меньше количество.

Билет