Б) Найдите площадь полученного сечения.
А) Постройте сечение куба этой плоскостью.
Решение.
Пусть 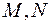 - середины ребер
- середины ребер 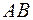 и
и 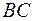 .
.
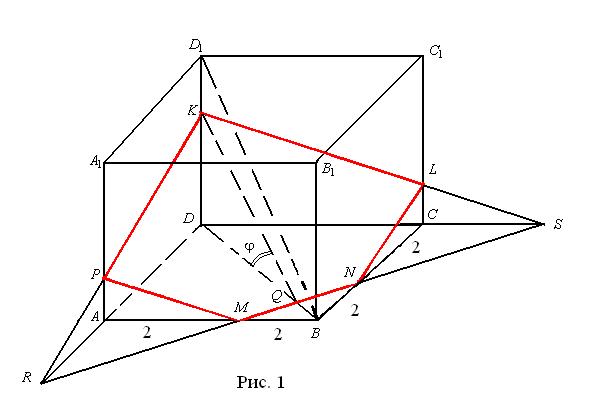
В плоскости  из точки Q пересечения прямой
из точки Q пересечения прямой 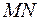 и диагонали
и диагонали 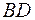 проведем прямую, параллельную диагонали
проведем прямую, параллельную диагонали 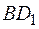 до пересечения с ребром
до пересечения с ребром 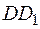 . Получим точку
. Получим точку 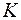 . Продолжим
. Продолжим 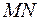 до пересечения с продолжением сторон
до пересечения с продолжением сторон  и
и  . Получим точки
. Получим точки 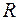 и
и 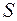 . Соединим полученные точки с точкой
. Соединим полученные точки с точкой 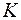 . Точки пересечения прямых
. Точки пересечения прямых 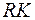 и
и 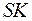 с ребрами
с ребрами 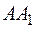 и
и 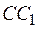 обозначим через
обозначим через 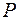 и
и 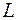 соответственно. Сечение
соответственно. Сечение 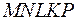 - искомое (Рис. 1).
- искомое (Рис. 1).
б) Воспользуемся формулой
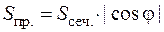 ,
, 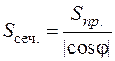
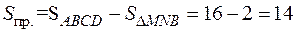 (Рис. 2).
(Рис. 2).
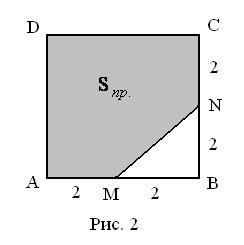
Прямая 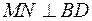 . Следовательно,
. Следовательно, 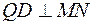 , причем
, причем 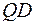 является проекцией наклонной
является проекцией наклонной 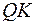 на плоскость основания куба
на плоскость основания куба 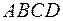 . По теореме, обратной теореме о трех перпендикулярах, наклонная
. По теореме, обратной теореме о трех перпендикулярах, наклонная  . Значит, угол
. Значит, угол 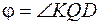 - искомый угол между плоскостью сечения и основанием (Рис. 1).
- искомый угол между плоскостью сечения и основанием (Рис. 1).
Вынесем диагональное сечение 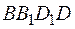 куба на отдельный чертеж (Рис. 3).
куба на отдельный чертеж (Рис. 3).
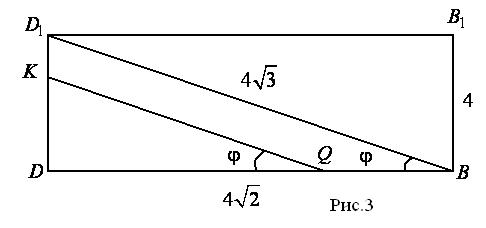
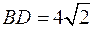 - диагональ квадрата основания куба.
- диагональ квадрата основания куба.
 - диагональ куба.
- диагональ куба.
Из 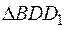 имеем:
имеем:
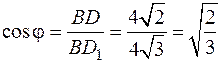 .
.
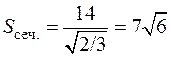 . Ответ:
. Ответ: 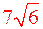 .
.
Пример 2.
В правильной четырех угольной пирамиде 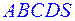 с вершиной
с вершиной 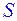 все ребра равны 6. Точки
все ребра равны 6. Точки 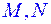 - середины ребер
- середины ребер 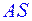 и
и  соответственно. Через точки
соответственно. Через точки 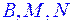 проведена плоскость.
проведена плоскость.