Метод контурных токов (МКТ)

Рассмотрим направленный граф схемы электрической цепи (рис.5.6), токи в ветвях которой требуется определить.

Дерево графа выделено на рисунке утолщенными линиями. Предположим, что известны токи в ветвях цепи, соответствующих связям в графе (ветви 1,2,3). Тогда токи в ветвях цепи, соответствующих ветвям дерева (ветви 4,5,6) могут быть найдены через токи связей из уравнений, составленных по первому закону Кирхгофа для узлов цепи: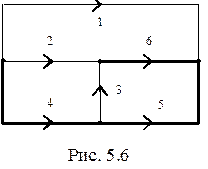

 

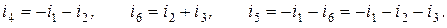
Нетрудно убедиться, что возможность выразить токи в ветвях дерева графа через токи в связях имеет место при любом выборе дерева графа. Таким образом, по известным токам в ветвях цепи, соответствующих связям графа, токи в остальных ветвях цепи могут быть определены, исходя из первого закона Кирхгофа без решения системы уравнений.

Токи связей будем называть в дальнейшем контурными токами. Такая терминология представляется естественной, поскольку именно связи определяют систему независимых контуров графа.

Метод контурных токов состоит в формировании уравнений электрической цепи только относительно токов связей (контурных токов). Система уравнений, составленная по методу контурных токов для схемы с 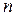независимыми контурами, имеет вид:

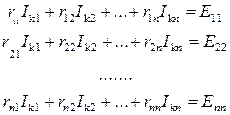
Здесь: - собственное сопротивление -го контура, - общее сопротивление -го и -го контуров, 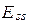- контурная э.д.с. -го контура, 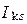- контурный ток -го контура (ток -ой связи).

Для уяснения правил формирования коэффициентов системы уравнений и ее правых частей рассмотрим следующий пример.

Определим токи в ветвях схемы, изображенной на рис.5.7а.

 

 

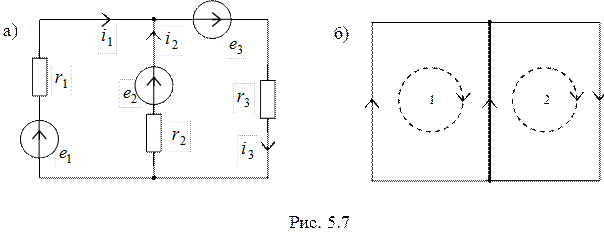
Изобразим направленный граф этой схемы (рис. 5.7б), включающий в себя два независимых контура. Схема содержит три ветви ( 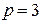) и два узла ( 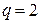) и уравнения, записанные для нее по законам Кирхгофа, имеют вид

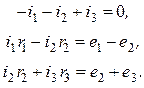
Исключим из рассмотрения одну из неизвестных - ток ветви дерева 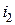, и, группируя подобные члены, получим

(*)

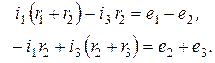В соответствии с изложенным выше, токи связе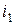й и 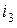являются кон-турными токами, то есть 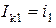и 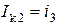. Система уравнений (*) принимает характерный для метода контурных токов вид

(**)

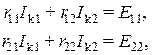если записать:

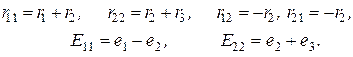
Заметим, что при другом выборе направления обхода одного из контуров (например второго), уравнения (*) примут вид

(***)

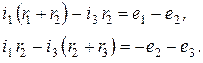Вводя в этом случае обозначения

придем снова к системе уравнений (**).

Таким образом, при любом выборе направления обхода независимых контуров (соотношения * и ***) стандартная форма записи уравнений метода контурных токов (**) достигается при выполнении следующих правил:

· собственное сопротивление контура определяется как сумма сопротивлений ветвей, входящих в этот контур;

· общее сопротивление контуров представляет собой сопротивление общей ветви контуров и , причем оно положительно, если контурные токи протекают по общей ветви в одну сторону и отрицательно - в противном случае;

· контурная э.д.с представляет собой алгебраическую сумму э.д.с., входящих в контур, при этом знак каждого слагаемого определяется совпадением (+) или не совпадением (-) направления источника и направления обхода контура.

Решив сформированную относительно контурных токов систему, нетрудно записать выражения для токов ветвей. В рассматриваемом примере (обход контуров по часовой стрелке) имеем

Основное достоинство метода контурных токов состоит в том, что он позволяет расчленить задачу определения токов в ветвях на два этапа. На первом из них решается система уравнений ( 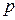- число ветвей схемы, - число ее узлов), записанная относительно токов в связях, на втором - токи ветвей дерева определяются по найденным на предыдущем этапе токам связей.

Решение системы алгебраических уравнений МКТ можно проводить с использованием теории определителей.

В качестве примера определим МКТ токи в ветвях схемы, которая вместе с ее графом изображена на рис.5.8

В данной схеме , , . Система уравнений имеет вид

Здесь:

Решение системы определяют соотношения:

где - главный определитель системы

а , , ... - алгебраические дополнения, получаемые из путем вычеркивания в последнем -ой строки и -го столбца и умножения вновь полученного определителя на . Отмечая справедливость равенства (поскольку ), в данном случае получим:

и так далее.

Главный определитело с тем, что граф схемы, на основе которого формируются независимые контуры, не содержит ветвей с источниками тока. Учесть наличие в цепи источников тока можно таким образом: неидеальные источники тока заменяются эквивалентными источниками э.д.с., идеальные - устраняются переносом вдоль контура. Указанные рекомендации иллюстрируют схемы, изображенные на рис.5.9, для последней из которых формируются уравнения МКТ.

 

 

При формировании уравнений метода контурных токов в схеме, содержащей зависимые источники, их учитывают вначале как независимые. Затем управляющие токи и напряжения выражаются через контурные токи, используя уравнения Кирхгофа и компонентные уравнения. После этого слагаемые из правой части системы, содержащие контурные токи, переносятся влево от знака равенства.

В качестве примера сформируем систему уравнений по методу контурных токов для схемы, изображенной вместе с ее графом на рисунке

В данной задаче количество ветвей , узлов , независимых контуров . Тогда можем записать

где

Выразим управляющие переменные и через контурные токи

после чего подставим сформированные коэффициенты и правые части в систему контурных уравнений

Перенесем слагаемые, содержащие контурные токи, из правой части системы в левую:

Таким образом, получена система уравнений МКТ, коэффициенты которой учитывают наличие в схеме зависимых источников.