Волновое сопротивление

Рассмотрим обтекание профиля при числах Маха 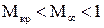. В этом диапазоне чисел возникают зоны местных сверхзвуковых скоростей, замыкающиеся скачками уплотнения, необратимые потери механической энергии в которых вызывают дополнительное волновое сопротивление.

Физическая природа волнового сопротивления. Рассмотрим схему обтекания профиля закритическим потоком (рис. 8.8). На верхней поверхности симметричного профиля при нулевом угле атаки приведена схема течения, а на нижней – соответствующая ей эпюра давления.

В передней критической точке скорость течения , а давление . При удалении от передней критической точки давление уменьшается, а скорость течения увеличивается. В точке А профиля и . Далее вниз по потоку скорость течения становится сверхзвуковой и продолжает расти, а давление уменьшается. Непосредственно перед скачком и . За скачком уплотнения скорость течения становится дозвуковой, давление , и при приближении к задней кромке скорость течения продолжает изоэнтропически уменьшаться до нуля, а давление возрастает до давления заторможенного за скачком уплотнения потока.

Если бы в рассмотренном диапазоне скоростей было возможно только изоэнтропическое обтекание (без скачков), то давление в кормовой части профиля было бы выше и равно . Скачок уплотнения приводит к понижению давления в кормовой части, что и обусловливает появление дополнительного, так называемого волнового, сопротивления.

Волновое сопротивление тем больше, чем больше потери полного давления в скачке. Величина коэффициента волнового сопротивления зависит от числа Маха перед скачком уплотнения. Чем больше , тем меньше коэффициент восстановления полного давления , т. е. больше потери и больше коэффициент волнового сопротивления.

Приближенный метод определения волнового сопротивления. Рассмотрим профиль со скачком на верхней поверхности (рис. 8.9). Выделим элементарную струйку, проходящую через скачок уплотнения. Проведем на расстоянии, достаточно удаленном от профиля, две контрольные поверхности I–I и II–II.

Параметры течения на поверхности I–I – , а на II–II – .

Из условия постоянства расхода следует: = , где dy – элемент длины вдоль контрольной поверхности. Применяя теорему о количестве движения к массе газа, заключенной между контрольными поверхностями, получаем следующее:

где – волновое сопротивление. С учетом уравнения неразрывности и принимая во внимание, что , выражение для запишем как

Во всех струйках, не пересекающих скачок уплотнения, и . Тогда для определения величины силы сопротивления интегрирование можно производить только по длине скачка. Считая , получаем: . Но так как , а также учитывая, что и , получаем . Поскольку , то , и при уменьшении величины коэффициента восстановления полного давления (с увеличением числа Маха и интенсивности скачка) сила волнового сопротивления возрастает.

После некоторых преобразований можно получить выражение для коэффициента волнового сопротивления профиля:

(8.2)

где А – постоянный коэффициент, который в общем случае зависит от формы профиля (для большинства современных профилей А ).

Формулой (8.2) можно пользоваться до . Из нее следует, что при заданном уменьшение возможно путем увеличения .

Особенности обтекания крыла конечного размаха

дозвуковым потоком

Аэродинамические характеристики крыла конечного размаха зависят как от формы сечения (профиля), так и от формы крыла в плане.

Рассмотрим крыло конечного размаха. Заметим, что характеристики сечений крыла различны из-за влияния перетекания воздуха через боковые кромки крыла. Профиль, а значит и крыло, создает подъемную силу только тогда, когда циркуляция вектора скорости вокруг профиля . То есть, по своему действию можно заменить систему профилей, составляющих крыло, присоединенным вихрем. Заменим крыло простейшей вихревой системой – одним П-об-разным присоединенным вихрем (рис. 8.10).

Циркуляцию скорости Г присоединенного вихря в данной задаче определим исходя из условия равенства подъемной силы крыла силе, создаваемой П-образным вихрем: , т. е.

, (8.3)

где – расстояние между свободными полубесконечными вихрями, сбегающими с концов крыла. Это расстояние больше размаха крыла на некоторую величину: . Можно принять, что .

Каждый свободный концевой вихрь индуцирует вокруг себя поле скоростей. Профили скорости для левого и правого концевых вихрей, а также эпюра суммарной скорости приведены на рис. 8.10. При начале координат в центре крыла величина скорости, индуцируемой обоими вихрями и направленной вниз, может быть определена по формуле Био–Савара для полубесконечного вихря как

. (8.4)

Средняя по размаху крыла скорость или с учетом выражения (8.4) после интегрирования получим

. (8.5)

Подставив значение циркуляции из уравнения (8.3), учтем, что , и проведем замену (удлинение крыла). Тогда при получим , и из формулы (8.5) следует, что

. (8.6)

Анализ формулы (8.6) показывает, что за появление индуцированной скорости ответственны подъемная сила и конечность крыла (для реального крыла ). Индуктивная скорость изменяет действительный угол атаки крыла (рис. 8.11), поскольку вблизи поверхности крыла скорость течения .

Скорость перпендикулярна вектору 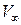, и ее называют скоростью скоса потока. Действительный вектор скорости отклоняется от вектора скорости набегающего потока на угол скоса .

Ввиду малости угла скоса, . С учетом формулы (8.6)

. (8.7)

Допустим, что крыло установлено под углом к вектору скорости набегающего потока (установочный угол атаки). Вследствие скоса потока истинный угол атаки крыла равен . Чем больше удлинение крыла , тем меньше скос потока и меньше различие между истинным и установочным углами атаки.

Создаваемая крылом подъемная сила , перпендикулярная вектору местной скорости , дает составляющую на направление скорости набегающего потока. Поскольку появление этой составляющей спровоцировано скосом потока за счет индуцированных концевыми вихрями скоростей, то ее принято называть силой индуктивного сопротивления. В соответствии с рис. 8.11 можно записать выражения для коэффициентов подъемной силы и индуктивного сопротивления: .

Ввиду малости и . С учетом выражения (8.7) для угла скоса потока, получим

. (8.8)

Формула (8.8) показывает, что индуктивное сопротивление обязано своим появлением подъемной силе – главной цели создания крыльев – и конечности размаха крыла. Индуктивное сопротивление и коэффициент индуктивного сопротивления равны нулю при нулевой подъемной силе ( ) или при .

Линеаризованная теория обтекания плоской пластинки

сверхзвуковым потоком

Рассмотренная ранее схема линеаризации течений разрежения и уплотнения (см. гл. 5) позволяет просто решить задачу обтекания плоской пластинки при малых углах атаки a.

Рассмотрим обтекание плоской пластинки, расположенной под малым углом атаки к вектору скорости набегающего потока (жидкость идеальная). В сверхзвуковом потоке малые возмущения против вектора скорости не распространяются, поэтому на плоскую пластинку набегает невозмущенный поток и обтекание ее верхней и нижней поверхностей можно рассматривать независимо друг от друга (рис. 8.12).

Линия тока, направленная вдоль верхней поверхности, испытывает в носовой части возмущение в виде разрежения , а в кормовой части – в виде сжатия . Для нижней поверхности порядок следования возмущений противоположный .

Так как между передней и задней кромками обеих поверхностей нет источников возмущения, то скорости потока и давления на этих поверхностях постоянны и равны и . Для нахождения давлений и коэффициентов давлений воспользуемся полученными ранее формулами (5.10) и (5.10а) для линеаризованного течения, подставляя в них и учитывая, что для верхней поверхности , а для нижней . Тогда

, , (8.9)

, . (8.9а)

В дозвуковом потоке 75 % подъемной силы создается за счет разрежения на верхней поверхности, и только 25 % – за счет повышенного давления на нижней. В сверхзвуковом потоке (рис. 8.13), в отличие от дозвукового, как следует из формул (8.9), (8.9а) давление вдоль верхней и нижней поверхностей пластинки распределяется равномерно (рис. 8.13, а), а центр давления располагается посредине пластины: . В дозвуковом потоке . Так как коэффициенты давления (рис. 8.13, б), то по линейной теории в сверхзвуковом потоке подъемная сила создается в одинаковой мере верхней и нижней поверхностями.

а б

Рис. 8.13. Распределение давления и коэффициента давления

по верхней и нижней сторонам пластинки:

а – давления; б – коэффициента давления

Найдем нормальную силу, которая действует на пластину:

Тогда подъемная сила равна (рис. 8.14), а волновое сопротивление (другие виды сопротивления отсутствуют, так как жидкость идеальная, а пластинка имеет бесконечный размах).

При малых углах атаки и . Отсюда коэффициенты сил и . С учетом выражений (8.9а) для коэффициентов давлений получаем

, . (8.10)

Следует помнить, что в этих формулах угол измеряется в радианах.

При малых углах атаки (см. рис. 8.2, зависимости от на линейном участке) , т. е. для плоской пластинки

. (8.10а)

Как следует из формул (8.10), (8.10а) с ростом числа коэффициенты , и уменьшаются.

Момент аэродинамической силы относительно передней кромки равен (положительным считается момент на кабрирование, т. е. на увеличение ). Коэффициент момента

ведет себя таким же образом, как и другие аэродинамические коэффициенты: при увеличении числа коэффициент момента уменьшается.