Арифметические операции, выполняемые в позиционных СС

Все операции в компьютере выполняются в арифметико-логическом устройстве (АЛУ). Числа, которые участвуют в операциях, называются операндами. Основная операция, которую выполняет АЛУ, операция сложения. Операции сложения в АЛУ выполняет функциональный узел –сумматор.

Операция вычитания заменяется сложением операндов в обратном или дополнительном кодах.

Операции умножения и деления сводятся к многократному сложению и переносам.

В вычислительной технике наибольшее применение имеет операция сложения. Вычисления выполняются по следующим правилам:

· операция сложения выполняется поразрядно, начиная с младших раз­рядов в слагаемых;

· в каждом одноименном разряде слагаемых суммируются соответ­ствующие цифры и перенос из предыдущего разряда суммы;

· если сумма цифр одноименных разрядов слагаемых и переноса мень­ше основания системы, то перенос в следующий разряд равен нулю, если равна или больше — то перенос равен единице.

Цифры суммы могут быть определены толь­ко последовательно, начиная с младших разря­дов. Это имеет принципиальное значение, так как в соответствующих суммирующих схемах вычис­лительной машины операции суммирования также должны выполняться последовательно, а это су­щественно увеличивает время вычисления суммы.

Ø Поразрядные операции.

Поразрядные операции — операции, кото­рые осуществляются над одноименными разрядами чисел незави­симо от соседних разрядов. Рассмотрим некоторые из них.

Поразрядное дополнение (или операция получения инверсного кода) — операция, по которой набор х₀ х₁ х₂ … х_n превращается в набор … , где = 1 – x_n, применяется для получения об­ратного кода отрицательного числа.

Поразрядное сложение двух чисел заключается в сложении од­ноименных разрядов чисел по модулю 2 в соответствии с правилом

0 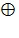0 = 0, 0 1 = 1, 1 0=1, 1 1=0;

применяется для сравнения двух чисел на равенство.

Поразрядное логическое сложение заключается в сложении од­ноименных разрядов двух чисел в соответствии с правилом

0 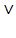0 = 0, 0 1 = 1, 1 0= 1, 1 1 = 1,где символ означает логическое сложение.

Поразрядное логическое умножение заключается в умножении одноименных разрядов двух чисел в соответствии с правилом

0 ^ 0 = 0, 0 ^ 1= 0, 1 ^ 0 = 0, 1 ^ 1 = 1.где символ ^ означает логическое умножение.

Поразрядные операции логического сложения и умножения при­меняют для модификации команд и чисел.

Ø Операции сдвига.

Операции сдвига заключаются в одновремен­ном смещении цифр числа (набора) на фиксированное число раз­рядов влево и вправо. В ЭВМ используется сдвиг логический, циклический и арифметический.

Логический сдвиг — смещение всей числовой последовательно­сти (слова), включая разряд знака, при котором в освободившиеся при сдвиге k разрядов устанавливаются нули.

Например, исходный набор х₀ х₁ х₂ … х_n при сдвиге на k разрядов вправо преобразуется в набор:

00….0 х₀ х₁ х₂ … х_n , где k — константа сдвига.

k

Циклический сдвиг — смещение всей числовой последовательно­сти (слова), при котором цифры, выходящие за пределы разрядной сетки, снова вводятся в освобождающиеся позиции слова.

Арифметический сдвиг — сдвиг всей числовой последовательно­сти (слова) без изменения позиции знака числа. Различают две разновидности арифметического сдвига: простой и модифицирован­ный. Простой арифметический сдвиг эквивалентен умножению числа, представленного в определенной системе счисления, на ос­нование этой системы счисления, возведенное в степень (положи­тельную или отрицательную), равную величине сдвига (константе сдвига).

Простой арифметический сдвиг влево для чисел в разных кодах характеризуется следующими особенностями.

Для прямого кода влево сдвигается только цифровая часть чис­ла, освобождающиеся младшие разряды заполняются нулями. До­пустимая величина константы сдвига k_д определяется числом под­ряд стоящих нулей после фиксированной запятой (точки).

Для дополнительного и обратного кодов влево сдвигается вся числовая последовательность, освобождающиеся младшие разряды для дополнительного кода заполняются нулями, для обратного — единицами. Для дополнительного кода выдвигающаяся единица из знакового разряда теряется, а для обратного кода должна быть направлена в младший разряд цифровой части (как для цикличе­ского сдвига влево). Допустимая величина константы сдвига k_д определяется числом подряд стоящих единиц после запятой (точ­ки).

Пример:

Выполнить простой арифметический сдвиг влево на один разряд чисел, заданных в разных кодах: х₁ = 1.0011; х₂ = 1.10001; xз = 1.1101.

Константа сдвига: k_д = 2 k_д=1 k_д = 2

После сдвига влево получим: х₁ = 1.0110; х₂ = 1.0001; х₃ = (1) 1.1011,

Простой арифметический сдвиг вправо для чисел в разных ко­дах характеризуется следующими особенностями.

Для прямого кода вправо сдвигается только цифровая часть числа.

Для дополнительного и обратного кодов вправо сдвигается вся числовая последовательность, цифра знакового разряда перемеща­ется в старший цифровой разряд и в то же время восстанавливает­ся в знаковом разряде.

При сдвиге вправо разряды чисел, выходящие за правую гра­ницу разрядной сетки, теряются. Так как число разрядов в разряд­ной сетке конечно, то в результате сдвигов может образоваться «машинный» нуль (исключением является результат неограничен­ного сдвига вправо отрицательного числа в дополнительном коде).

Пример:

Выполнить простой арифметический сдвиг вправо на один разряд чисел, заданных в разных кодах: х₁ = 1.00110; х₂ = 1.10110; х₃ = 1.11010.

После сдвига вправо получим: х₁'= 1.00011; х₂^∙ = 1.11011; х₃' = 1.11101.

Модифицированный арифметический сдвиг используется для чи­сел с плавающей запятой (точкой). Для такого сдвига величина исходного числа после сдвига не изменяется, т. е. в этом случае на­ряду со смещением мантиссы числа одновременно изменяется и его порядок так, чтобы величина числа осталась без изменений.

Ø Арифметические операции над числами в двоичной СС

Рассмотрим правила выполнения арифметических операций над однораз­рядными числами.

Правило сложения 0 + 0 = 00 0 + 1 = 01 1 + 0 = 01 1 + 1 = 10 Перенос 1 в ст. разряд

Правило вычитания 0 – 0 = 0 1 – 0 = 1 1 – 1 = 0 10 – 1 = 1 Заем 1 из ст. разряда

Правило умножения 0 х 0 = 0 0 х 1 = 0 1 х 0 = 0 1 х 1 = 1

Правило сложения по модулю 2 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 0

 

Рассмотрим несколько примеров выполнения арифметических дей­ствий над многоразрядными числами в двоичной СС.

Примеры.

1. Сложить два двоичных числа А=10100110 и В=00101111 (166₁₀ + 47₁₀):

Сложение двух многоразрядных двоичных чисел проводится поразрядно с учетом единиц переполнения от предшествующих разрядов.

Перенос в ст.разр. 1 1 1 1 11

1-е слагаемое 1 0 1 0 0 1 1 0 166

2-е слагаемое + 0 0 1 0 1 1 1 1+ 47