Числа с плавающей запятой

Вычислительные системы широко используют представление чисел с плавающей точкой. Идея этого представления состоит в том, чтобы нормализовать позиционную двоичную дробь, избавившись от незначащих старших нулевых битов освободив место для (возможно) значащих младших разрядов. Сдвиг, который нужен для нормализации, записывается в битовом поле, называемое порядком. Само же число называется мантиссой.

Пример.Число 0072.3500₍₁₀₎ -до нормализации и 0,7235х10² -после.

В двоичной СС запись будет следующей: до нормализации -001001000,100011 и после -1001000100011 х 2⁷

Целая часть Дробная часть

До нормализации

15 6 5 0

После нормализации

Порядок =7 мантисса

В форме представления с плавающей запятой (точкой) число изображается в виде двух групп цифр:

• мантисса;

• порядок.

При этом абсолютная величина мантиссы должна быть меньше 1, а порядок должен быть целым числом.

Например, приведенные ранее числа в нормальной форме запишутся следующим образом:

+0,721355 х 10³;

+0,328 х 10^-3;

-0,103012026 х 10⁵.

Нормальная форма представления обеспечивает большой диапазон отображения чисел и является основной в современных компьютерах.

В форме с плавающей запятой числа представляются в виде произведений:

C = q^П ∙M = X∙ M (1.7)

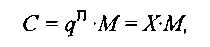
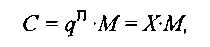где q — основание системы счисления (обычно целая степень числа 2);

П — порядок числа длиной k+1 (целое число со знаком, где к –число знач.цифр);

М— мантисса числа длиной г +1 (правильная дробь со знаком);

X - характеристика числа.

Знак всего числа определяется знаком мантиссы.

Для мини-компьютеров основания порядка и мантиссы совпадают (далее предполагается этот случай), а для больших машин — они различны. Представление числа формулой (1.7) называют также полулогарифмическим, потому что только часть числа — характеристика — представляется в логарифмической форме.

Следует заметить, что все числа с плавающей запятой хранятся в машине в так называемом нормализованном виде.

Нормализованным называют такое число, старший разряд мантиссы которого больше нуля. У нормализованных двоичных чисел, следовательно, 0,5 < │М│< I.

Нормализованные, т. е. приведенные к правильной дроби, числа:

10,35₁₀ = 0,1035₁₀x 10⁺²;

0,00007245₈= 0,7245₈х 8 ^-4;

F5C,9B₁₆= 0,F5C9B₁₆x 16⁺³;

В памяти ЭВМ числа с ПТ хранятся в двух форматах:

• слово — 32 бита, или 4 байта;

• двойное слово — 64 бита, или 8 байт.

Разрядная сетка для чисел с ПТ имеет следующую структуру:

• нулевой разряд — это знак числа (0 — «минус», 1 — «плюс»);

• с 1 по 7 разряд записывается порядок в прямом двоичном коде, пустые разряды заполняются нулями. В первом разряде указывается знак порядка (1 — «плюс» или 0 — «минус»);

• с 8 по 31 (63) указывается мантисса, слева направо без нуля целых в прямом двоичном коде и для отрицательных чисел и пустые разряды заполняются нулями.

Мантисса называется нормализованной, если ее значение определяется неравенством вида

≤ |M| < 1 т.е. для основания q = 2 имеем: 0,5 < М< 1.

Пример 1.3 Иллюстрация записи числа с плавающей запятой: А₂ = 2¹∙110,111 = 2²∙11,0111 = 2⁴∙0,110111

то есть в старшем разряде модуля мантиссы должна быть записана единица.

Значение порядка (П = 1, 2 и 4) указывает на количество позиций, на которые "плавает" запятая.

Формат числа с плавающей запятой в 16-разрядной сетке показан на рис. 1.8. Тут для модулей порядка и мантиссы отведено соответственно пять (с 10 по 14) и девять (с 0 по 8) разрядов. Запятая в порядке размещена (условно) после младшего разряда, а в мантиссе — перед старшим. Знаки порядка и мантиссы размещены перед их старшими разрядами.

15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 Нумерация разрядов числа

+/-

Порядок

+/-

Мантисса

Рисунок 1.8 –Формат чисел в форме плавающей запятой

Абсолютное значение числа С в форме с плавающей запятой с учетом формул (1.7), (1.9) и (1.13) изменяется в пределах

X_min M_min = C_min ≤ |C| ≤ C_max = X_max M_max (1.8)

где X_min =2^-П^max ( П_max = 2^r -1, где r –разрядность модуля порядка )

M_min =2^-1

X_max =2^+П^max

M_max =1-2^-^k (k –разрядность модуля мантиссы)

Диапазон представления чисел в форме с плавающей запятой

Пример 1.4 Рассчитать значение диапазона Д_C для числа С при г = 5, к = 9. С учетом выражения (1.15) получаем: если П_max = 2^r -1= 2⁵ – 1 = 31 то D_C =2^+П^max⁺¹ =2³¹⁺¹= 2³² что приблизительно соответствует десятичному числу 10^32∙0,3 ≈ 10⁹. Диапазон представления чисел с плавающей запятой приблизительно больше в П_max раз диапазона представления чисел в форме с фиксированной запятой.

D_C = 2C_max = 2∙ 2^+П^max(1-2^-^k) ≈2^+П^max⁺¹ (1.9)

Абсолютная погрешность представления чисел в форме с плавающей запятой зависит от погрешности мантиссы и порядка числа:

∆С = ∆М∙2^±^П; ∆М =2⁽^k⁺¹⁾ (1.10)

где ∆M— погрешность представления мантиссы.

Минимальная и максимальная относительные погрешности представления чисел в форме с плавающей запятой не зависят от характеристики (она записывается в числителе и знаменателе выражения и потому сокращается).

С учетом формул (1.14) и (1.16) относительные погрешности рассчитывают из соотношений:

δC_min = = = 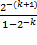2^-(k+1) ; δC_max = 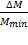= = 2^-k (1.11)

Из выражений (1.17) следует, что относительные погрешности представления чисел в форме с плавающей запятой практически постоянны во всем диапазоне чисел.

1.4 Представление информации в микропроцессорах класса Pentium

Рассмотрим представления операндов в 32-разрядных микропроцессорах класса Pentium. В них используются такие типы данных: целые числа, вещественные числа, двоично-десятичные числа и строки битов, байтов и слов. Целые числа представляются со знаком и без знака в форматах байта, полуслова, слова, двойного и учетверенного слова длиной соответственно 8, 16, 32, 64 и 128 бит (рис. 1.9).

31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0

+/- байт

+/- Полуслово

+/- Слово

Рисунок 1.9 – Форматы целых чисел со знаком

Над числами в этих форматах выполняются операции сложения, вычитания, умножения, деления. Диапазоны представления знаковых и беззнаковых значений в данных форматах представлены в табл. 1.4.

Формат числа Диапазон представления чисел

без знака со знаком

Байт 0...255 -128. .. + 127

Полуслово 0...65535 -32768...+32767

Слово 0...4∙10⁹ -2∙10⁹...+2∙10⁹

Двойное слово 0...5∙10'⁹ -2,5∙10^,9...+2,5∙10¹⁹

Вещественные числа представлены в формате с плавающей запятой в коротком (32 бит), длинном (64 бит) и расширенном (80 бит) форматах (рис. 1.10). Числа с плавающей запятой длиной 32 и 64 бит, которые используются во многих компьютерах, обычно называют числами с одинарной (32разряда) и двойной точностью (64 разряда).

Расширенный формат (80 разрядов) характерен только для процессоров класса Pentium.

31 30 24 23 0

+/- Порядок = 8 Мантисса (24 бит)

63 62 53 52 0

+/- Порядок (11 бит) Мантисса (53 бит)

79 78 64 63 0

+/- Порядок (15 бит) Мантисса (64 бит)

Рисунок 1.10 – Форматы чисел с плавающей запятой: короткий, длинный и расширенный

В данных форматах чисел с плавающей запятой используются смещенные порядки П_СМ:

П + 127 для r = 8

П_СМ = П + ∆П = П + 2^r^-1 – 1 =П + 1023 для r = 11

П + 16383 для r = 15

Где: П — значение истинного порядка;

∆П = 2^Г-' - 1 — смещение;

г — длина порядка, которая равна 8, 11 или 15 бит соответственно для короткого, длинного и расширенного формата.

Значение П_СМ всегда положительное, поэтому знаковый разряд не нужен. Представление порядка со смещением упрощает операции сравнения чисел с плавающей запятой, что особенно важно для алгоритмов сортировки.

Значение числа с плавающей запятой и смещенным порядком определяется по формуле

С = (-1)^S (F₀ , F₁ , . . . F_i , . . . F_n)

где S — знак числа; п — число, которое для разных форматов равно 23, 52 или 63.

В машине мантисса представлена в нормализованной форме, которая состоит из целой части F₀ = 1 и дроби в таком виде:

M = 1, F₁ , F₂ , . . . F_i , . . . F_n

В коротком и длинном форматах бит F₀ при передаче чисел и хранении их в памяти не фигурирует. Это — скрытый (неявный) бит, который в нормализованном числе всегда равен единице.

Пример 1.5 Представить десятичное число -247,375 в коротком формате. Двоичный код этого числа равен -11110111,011; истинный порядок будет +7 (запятая сдвигается влево на семь разрядов), а смещение достигнет значения П_см = 127 + 7 = 134. С учетом скрытого бита F₀ - 1 имеем: Знак Порядок Мантисса 1 10000110 ,1110 1110 1100 0000 0000 0000.

Параметры форматов вещественных чисел представлены в табл. 1.5.

Параметры Формат

короткий длинный расширенный

Длина формата, бит

Длина мантиссы, бит

Длина порядка, бит

Смещение порядка + 127 + 1023 +16383

Диапазон 10^±38 10^±308 10^±4932

Числа в коротком и длинном форматах существуют только в памяти. При загрузке чисел в одном из этих форматов в микропроцессор они автоматически преобразуются в 80-битный формат, который используется только для внутренних oneраций. Аналогично данные из процессора преобразуются в короткий или длинный формат для хранения в памяти.

Точность вычислений чисел с плавающей запятой возрастает с увеличением длины мантиссы. Диапазон представления чисел с плавающей запятой зависит от длины порядка и основания счисления q. В машинах ЕС ЭВМ значение q = 16. В процессорах Pentium диапазон представления чисел в коротком формате для q = 2 находится в пределах 10^±³⁸. Если же для этого формата взять основание q = 16, то получим значение диапазона в пределах 10^±¹⁵².

В микропроцессорах Pentium используются двоично-десятичные цифры в таких форматах:

• восьмиразрядные упакованные, которые содержат в одном байте две десятичные цифры в коде 8421, например, 39₁₀ = 0011 1001_2-10;

• восьмиразрядные неупакованные, которые содержат одну десятичную цифру в байте (младшая тетрада) вместе с признаком (зоной) 0011₂ в международном коде ASCII,

например, 49₁₀ = 0011 0100 0011 1001_2-10

Представление десятичного числа 136492 в неупакованном и упакованном форматах показано на рис. 1.11;

7 0 7 0 7 0 7 0 7 0 7 0

0011 0001 0011 0011 0011 0110 0011 0100 0011 1001 0011 0010 Неупакованный формат

0001 0011 0110 0100 1001 0010 Упакованный формат

Рисунок 1.11 – Представление десятичных цифр в различных форматах

• 80-разрядные упакованные, в которые записываются 19 десятичных цифр (19 тетрад), и в старшую тетраду (20 тетрада) записывается знак числа.

1.5 Информационные меры

В теории передачи и преобразования информации установлены информационные меры количества и качества информации — семантические, структурные, статистические.

Ø Семантический подход позволят выделить полезность или ценность информационного сообщения. В структурном аспекте рассматривают строение массивов информации и их измерение простым подсчетом информационных элементов или комбинаторным методом.

Ø Структурный подход используют для оценки возможностей информационных систем вне зависимости от условий их применения. При использовании структурных мер информации учитывают только дискретное строение сообщения, количество содержащихся в нем информационных элементов, связей между ними. При структурном подходе различают геометрическую, комбинаторную и аддитивную меры информации.

§ Геометрическая мера определяет параметры геометрической модели информационного сообщения (длина, площадь, объем) в дискретных единицах. Эту меру применяют как для оценки информационной емкости всей модели, так и для оценки количества информации в одном сообщении.

§ В комбинаторной мере количество информации I определяют количеством комбинаций элементов (символов), которые совпадают с числом:

• сочетаний из q элементов по п:

например, для множества цифр 1, 2, 3, 4 можно составить шесть сочетаний по две цифры: 12, 13, 14, 23, 24, 34;

• перестановок I = q!,

например, для множества букв а, в, с можно получить шесть перестановок: авс, асе, вас, вса, сав, сва;

• размещений с повторениями из q элементов по п:

Например, для q = 0, 1 и n = 3 имеем: 000, 001, 010, 011, 100, 101, 110, 111.

§ Широкое распространение получила аддитивная мера.

Пусть N—число равновероятных сообщений, п — их длина, q — число букв алфавита, используемого для передачи информации. Количество возможных сообщений длины п равняется числу размещений с повторениями

N = qⁿ. (1.11)

Эту меру наделяют свойством аддитивности, чтобы она была пропорциональна длине сообщения и позволяла складывать количество информации ряда источников. Для этого Хартли предложил логарифмическую функцию как меру количества информации (I):

I = log N = n log q. (1.12)

Количество информации, которое приходится на один элемент сообщения, называется энтропией (H).

H = I/n = log q. (1.13)

Основание логарифма зависит от выбора единицы количества информации. Если для алфавита используют двоичные цифры 0 и 1, то за основание логарифма принимают q = 2, в результате чего

I = n log₂ 2 = п.

При длине п = 1 получают I = 1 и это количество информации называют битом.

Передача сообщения длиной п = 1 эквивалентна выбору одного из двух возможных равновероятных сообщений — одно из них равно единице, другое — нулю. Двоичное сообщение длины п содержит п битов информации. Если основание логарифма равно 10, то количество информации измеряется в десятичных единицах — дитах, причем 1 дит = 3,32 бита.

Например, текст составлен из 32 букв алфавита и передается последовательно по телетайпу в двоичном коде. При этом количество информации I = log₂N = log₂32 = 5 битов.

Далее используются логарифмы с основанием два.

Ø В общем случае сообщения появляются с разной вероятностью. Статистическая мера использует вероятностный подход к оценке количества информации. Согласно Шеннону каждое сообщение характеризуется вероятностью появления, и чем она меньше, тем больше в сообщении информации. Вероятность конкретных типов сообщений устанавливают на основе статистического анализа.

Пусть сообщения образуются последовательной передачей букв некоторого алфавита:

х₁, ..., х_i ..., х_q

с вероятностью появления каждой буквы: р(х₁) = р₁, ..., p(x_i) =р_i ..., р(х_q) = р_q,

при этом выполняется условие: р₁ + ... + р_i + ... + р_q = 1.

Множество с известным распределением элементов называют ансамблем. Согласно Шеннону количество информации, которое содержится в сообщении х_i, рассчитывают по формуле:

Для абсолютно достоверных сообщений р_i = 1, тогда количество информации I(x_i) = 0; при уменьшении значения p_i количество информации увеличивается.

Пусть в ансамбле все буквы алфавита х₁, ..., х_i ... , х_q — равновероятны, то есть p₁ = р₂ = ... = р_q = 1/q, и статистически независимы. Тогда количество информации в сообщении длиной n букв с учетом выражения (1.4)

(1.14)

что совпадает с мерой Хартли в соответствии с выражениями (1.11) и (1.12).

Согласно Шеннону информация — это снятие неопределенности, что понимают следующим образом. До опыта событие (например, появление буквы х_i) характеризуют малой начальной вероятностью р_н, которой соответствует большая неопределенность. После опыта неопределенность уменьшается, поскольку конечная вероятность р_к > р_н. Уменьшение неопределенности рассчитывают как разность между начальным I_Hи конечным I_К значениями количества информации.

Например, для р_H = 0,1 и р_K = 1 получим:

∆I = I_H – I_K = log - log 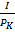= log 10 – log 1 = 3.32

Пусть сложное сообщение характеризуется алфавитом из букв х₁, х₂, ..., х_q, их вероятностями р₁, р₂, .... р_q и частотой появления каждой буквы m₁, m₂, ..., m_q. Все сообщения статистически независимы, при этом m₁, + m₂ + ... + m_q = m.

Общее количество информации для всех q типов сообщений с учетом выражения (1.14)

Среднее значение количества информации на одно сообщение (энтропия) согласно формуле Шеннона

где при большом значении m отношение m_i/m характеризует вероятность р_i каждой буквы. Выражение log1/p_i, рассматривают как частную энтропию, которая характеризует информативность буквы x_i, а энтропию Н— как среднее значение частных энтропии. При малых значениях p_i частная энтропия велика, а с приближением p_i, к единице она приближается к нулю (рис. 1.5, а).

Функция η = (Pi) = p_i log1/p, отражает вклад буквы х_i в энтропию Н. Как видим, при p_i = 1 эта функция равна нулю, затем возрастает до своего максимума и при уменьшении р_i приближается к нулю. Функция η(p_i) при значении p_i = 0,37 имеет максимум 0,531.

Интерес представляют сообщения с использованием двухбуквенного алфавита х₁ и х₂ (например, цифры 0 и 1).

Поскольку при q = 2 вероятность букв алфавита p₁ +p₂ = 1, то можно положить, что p₁ = р и р₂ = 1 -р. Тогда энтропию определяют соотношением:

(1.15)

график которой показан на рис.1.5, б. Он образуется суммированием двух графиков, определяющих энтропию каждой из двух букв. Из графиков видно, что при p = 0 или р = 1 энтропия равна нулю и неопределенность полностью снимается. Это означает, что с вероятностью, равной единице, можно знать, каким будет следующее сообщение.

Энтропия двухбуквенных сообщений достигает максимального значения, равного 1 биту, при р = 0,5, и ее график симметричен относительно этого значения. Это тот случай, когда наиболее трудно предугадать, какое сообщение будет следующим, — то есть ситуация наиболее неопределенная.

В общем случае энтропия обладает следующими свойствами.

1. Энтропия — величина вещественная, непрерывная, ограниченная и неотрицательная.

2. Энтропия равна нулю, если сообщение заранее известно. В этом случае некоторое сообщение задано с вероятностью р_i = 1, а вероятность остальных равна нулю.

3. Энтропия максимальна, если все сообщения равновероятны: р₁ =р₂ = ... = р_q = 1/q...

В этом случае на основании выражения (1.15) получим:

что совпадает с выражением (1.3). В этом случае оценки количества информации по Хартли и Шеннону совпадают.

4. При неравных вероятностях количество информации по Шеннону меньше меры Хартли.

5. При объединении энтропии двух независимых источников сообщений их энтропии складываются.

В компьютере наименьшей возможной единицей объемной (геометрической) меры информации является бит. Объем (или емкость) информации вычисляется по количеству двоичных символов 0 и 1, записанных в памяти компьютера. При этом возможно только целое число битов в отличие от вероятностного подхода, где может быть и нецелое число.

Для удобства использования введены также единицы количества информации, превышающие бит. Так, двоичное слово из восьми символов содержит 1 байт информации, 1024 байт составляют килобайт (Кбайт), 1024 Кбайт — мегабайт (Мбайт) и 1024 Мбайт — гигабайт (Гбайт); при этом 1024 = 2¹⁰

Между объемным и вероятностным количествами информации соотношение неоднозначное. Если сообщение допускает измерение количества информации и объемно и вероятностно, то они не обязательно совпадают. При этом вероятностное количество не может быть больше объемного. В дальнейшем тексте количество информации понимается в объемном значении.

Замечание

Международная система единиц измерения величин СИ (SI) устанавливает специальные приставки для получения кратных и дольных единиц измерения во всех областях науки и техники. Эти приставки имеют полные наименования и сокращенные обозначения и позволяют умножать значение основной единицы на определенную степень числа 10. Для удобства мы будем называть эти приставки десятичными. Приведем наиболее важные десятичные приставки.