Фиксированная запятая (точка).

Замечание.В русском языке принято называть разделитель целой и дробной части дроби запятой, а в английском – точкой. Поскольку современная вычислительная терминология формировалась на английском языке, то словосочетания «фиксированная точка» и «плавающая точка» вошли в русскую компьютерную лексику.

В форме представления с фикси­рованной запятой (точкой) числа изображаются в виде последова­тельности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной.

Например, для числа 1355,1875₍₁₀₎, что соответствует 010101001011,0011₍₂₎, запись следующая:

Целая часть Дробная часть

=1355 + 3/16

15 4 3 0

Представление числа с фиксированной точкой концептуально самое простое, берется двоичное число и объявляется, что определенная часть его младших разрядов представляет собой дробную часть в позиционной системе счисления.

Например, пусть числа представлены в десятичной системе счисления и имеют пять разрядов в целой части числа (до запятой) и пять в дробной части (после запятой).

Числа, записанные в такую разрядную сетку, имеют вид:

+00721.35500.

+00000.00328.

-10301.20260.

Диапазон значащих чисел N в системе счисления с основанием Р при наличии тразрядов в целой части и sразрядов в дробной части числа (без учета знака числа) будет таким:

P^-s ≤ N≤ P^m – Р^-s

Например, при Р=2, m=10 и s = 6 числа изменяются в диапазо­не 0,015 < N< 1024. Если в результате операции получится число, выходящее за допустимые пределы, произойдет переполнение раз­рядной сетки, и дальнейшие вычисления теряют смысл.

Положение запятой строго фиксировано и при этом предполагается:

- положение запятой закрепляется в определенном месте и сохраняется неизменным для всех чисел, изображаемых в принятой разрядной сетке машины;

- хотя запятая и фиксируется, но никак не выделяется в коде числа, а только подразумевается.

Обычно в ЭВМ используется два способа расположения запятой:

-перед старшим разрядом (Р=0);

-после младшего разряда (Р=n), где n –число разрядов, отводимых под цифровую часть числа. Во втором случае представляются только целые числа со знаком.

Выход исходных чисел, а также чисел, полученных в процессе вычислений, за пределы допустимого диапазона приведет к грубым ошибкам. Чтобы этого избежать, необходимо при разработке программ исходные числа масштабировать.

Недостатки. Имеет небольшой диапазон представления чисел и поэтому чаще всего неприемлема при вычислениях. В современных компьютерах естественная форма представления использу­ется как вспомогательная и только для целых чисел.

Достоинство. Эта форма наиболее проста, естественна и для представления чисел с фиксированной точкой можно построить сравнительно несложное арифметическое устройство с высоким быстродействием.

В памяти ЭВМ числа с фиксированной точкой хранятся в трех форматах:

а) полуслово — 16 бит, или 2 байта;

б) слово — 32 бита, или 4 байта;

в) двойное слово — 64 бита, или 8 байтов.

Отрицательные числа с ФТ записываются в разрядную сетку в дополнительных кодах, которые образуются прибавлением единицы к младшему разряду обратного кода. Обратный код получается за­меной единиц на нули, а нулей на единицы в прямом двоичном коде.

В числах со знаком выделяют дополнительный знаковый разряд (обычно, край­ний слева). В нем для знака плюс записывают цифру 0, а для знака минус — циф­ру 1. В числах без знака все разряды числа определяют модуль. Форматы двоичных дробных и целых чисел со знаком, с нумерацией разрядов справа налево и значением их веса показаны на рис. 1.7.

7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0 Нумерация разрядов

+/-

26

25

24

23

22

21

20

+/-

,

2-1

2-2

2-3

2-3

2-4

2-6

2-7

Форма байта для целого числа Форма байта для правильной дроби

Рисунок 1.7 – Формат байта

Числа в разрядную сетку записывают в соответствии с весом позиций. Не заня­тые разряды заполняют нулями, как это показано на рис. 1.8 для чисел +0,725₁₀ = +0,10111₂ и -47₁₀ = -101111₂.

7 6 5 4 3 2 1 0 7 6 5 4 3 2 1 0

,

Запись целого числа -101111₂ Запись правильной дроби +0,10111₂

Рисунок 1.8 – Запись чисел

Интервал числовой оси, заключенный симметрично между максимальным и минимальным значением числа, называется диапазоном представления.

Абсо­лютное значение целого числа А изменяется в пределах:

А_min ≤ | А | ≤ А_max А_min = 1; А_max = 2^k - 1, (1.1 )

где к— количество разрядов цифровой части числа.

Из выражения (1.1) следует, что числа, по абсолютному значению меньше еди­ницы, воспринимаются как "машинный нуль"; числа, больше А_max, вызывают пере­полнение разрядной сетки. Диапазон представления целых чисел с учетом симмет­рии относительно нуля числовой оси

Пример 1.1 Рассчитать максимальное значение и диапазон представления целого числа со знаком в 16-разрядной сетке. На основе выражений (1.1) и (1.2) для k = 15 по­лучаем: Аmax = 215 - 1 = 32767; D = 2Аmax = 65534.

D_A = 2A_max = 2(2^k-1) ≈ 2^k-1 (1.2)

Абсолютное значение правильной дроби В изменяется в пределах:

В_min ≤ | В | ≤ В_max В_min = 2^-k В_max = 1 - 2^k, (1.3)

Правильная дробь, по модулю меньше 2^-k, воспринимается как "машинный нуль"; числа, больше единицы, вызывают переполнение разрядной сетки.

Диапазон представления правильной дроби:

Пример 1.2 Рассчитать максимальное значение и диапазон представления правильной дроби в 16-разрядной сетке. На основе выражений (1.3) и (1.4) для k = 15 по­лучаем: Вmax = 1 - 215 = -32767 D = 2Вmax = -65534. .

D_B = 2B_пах = 2(1-2^-k) ≈ 2 (так как 1 >> 2^-k. ) (1.4)

Точность представления чисел в компьютере определяется абсолютной и от­носительной погрешностью.

Абсолютная погрешность ∆ представления чисел в ком­пьютере составляет:

для целых чисел: ∆А = 1/2 = 2^-1 где А –целое число (1.5)

для правильной дроби: ∆В = 2^k/2 = 2^-(k+1) где В –правильная дробь (1.6)

Из выражения (1.5) следует, что абсолютная погрешность представления це­лых чисел в форме с фиксированной запятой равна половине младшего разряда и не зависит от длины разрядной сетки. Из выражения (1.6) видно, что абсолютная погрешность представления правильной дроби в форме с фиксированной запятой уменьшается при увеличении длины разрядной сетки.

Относительная погрешность δ представления числа задается отношением аб­солютной погрешности к текущему значению числа и находится в пределах

δ_min ≤ δ ≤ δ_max

Для целых чисел в форме с фиксированной запятой минимальное и макси­мальное значения относительной погрешности

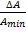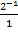δ_Amin = = ≈ 2^-(k+1) δ_Amax= = = 0,5

Такими же формулами определяются минимальное и максимальное значения относительной погрешности для правильной дроби с фиксированной запятой.

Отно­сительная погрешность представления чисел в форме с фиксированной запятой существенно зависит от значения числа и значительно возрастает для малых чисел.