Принятие решений в условиях неопределенности.

В данном разделе мы познакомимся с некоторыми методами принятия решений в условиях неполной информации, основанных на комбинации теоретико-вероятностных и игровых подходов.

Рассмотрим следующую задачу. Предположим, что Лицо, Принимающее Решение (ЛПР), имеет на выбор возможных стратегий. Прибыль, которую принесет ему каждое из возможных решений, зависит от того, какая ситуация сложится в будующем вокруг его проекта. Всего имеется таких возможных ситуаций, и соответствующая прибыль определяется матрицей последствий . Здесь есть велична прибыли, при условии, что принято –е решение и сложится 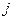–я ситуация. Если, дополнительно, известны вероятности 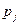реализации каждой из ситуаций , , то для каждой фиксированной стратегии , , прибыль становится случайной величиной со значениями , , 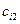¼, 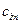и вероятностями 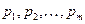соответственно. В этом случае ЛПР предлагается выбрать такую стратегию, которой соответствует максимальное среднее значение (математическое ожидание) случайной величины прибыли. Это критерий в теории принятия решений называется критерий наибольшего среднего ожидаемого значения. Если вероятности ситуаций равны между собой, , то этот частный случай критерия среднего значения называется критерием Лапласа.

Задача 9.1. Фирма может принять решение о строительстве небольшого или крупного предприятия. Небольшое предприятие можно через два года расширить. Доход фирмы при каждом принятом решении зависит от высокого или низкого спроса на продукцию. Известно следующее. Крупное предприятие при высоком спросе дает 15 млн.руб. в год, а при низком 3 млн.руб. в год. Небольшое предприятие при высоком спросе дает 8, а при низком спросе — 5 млн.руб. в год соответственно. Расширенное предприятие дает при высоком спросе 11 млн.руб. в год, а при низком 8 млн.руб. в год. Строительство крупного предприятия обойдется фирме в 75 млн.руб. Строительство небольшого предприятия обойдется в 15 млн.руб., а его расширение через два года — в 44 млн.руб. Анализ рыночной ситуации показывает, что вероятность высокого и низкого спроса равна соответственно 0.6 и 0.4 для первых двух лет эксплуатации предприятия, и равна 0.7 и 0.3 для последующих восьми лет. Таким образом, у фирмы имеется два этапа принятия решений: в начальный момент времени и через два года. Исходя из имеющихся данных, построить дерево решений для фирмы из расчета 10 лет эксплуатации и рассчитать вероятности каждого из состояний. Используя критерий среднего ожидаемого значения, определить оптимальное решение о строительстве для фирмы.

Решение.Построим дерево решений.

III

Таким образом, у лица, принимающего решения, всего имеется три стратегии.

I) Построить крупное предприятие

II) Построить мелкое предприятие

III) Построить мелкое предприятие и затем расширить его через 2 года.

Кроме того, имеется 4 различных рыночнаых комбинаций спроса:

1) высокий спрос на протяжении всех 10 лет;

2) высокий спрос в первые два года и низкий спрос в течение последующих 8 лет;

3) низкий спрос в первые два года и высокий спрос в послежующие 8 лет;

4) низкий спрос на протяжении всех 10 лет.

По условиям задачи, вероятности этих ситуаций вычисляются следующим

0.6×0.7=0.42 для ситуации №1:

0.6×0.3=0.18 для ситуации №2;

0.4×0.7=0.28 для ситуации №3;

0.4×0.3=0.12 для ситуации №4.

Найдем закон распределения случайной величины прибыли для каждого из трех возможных стратегий. Пусть сначала (строим крупное предприятие). Если 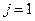, то мы получаем 15 млн.руб. в год в течение 10 лет при затратах 75 млн.руб. Чистая прибыль составит 150-75=75 млн.руб. Если , то мы получаем 15 млн.руб. в год в течение 2 лет и 3 млн.руб. в год в течение 8 лет. Чистая прибыль составит 30+24-75=-21 млн.руб (то есть предприятие приносит убытки). Если 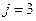, то мы получаем 3 млн.руб. в год в течение 2 лет и 15 млн.руб. в год в течение 8 лет. Чистая прибыль составит 6+120-75=51 млн.руб. Если , то мы получаем 3 млн.руб. в год в течение 10 лет. Чистая прибыль составит 30-75=-45 млн.руб (предприятие убыточно). Закон распределения случайной величины дохода определяется таблицей

		-21		-45
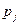
	0.42	0.18	0.28	0.12

Средний доход равен

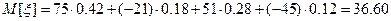Рассмотрим случай (строим малое предприятие без расширения). Если 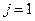, то мы получаем 8 млн.руб. в год в течение 10 лет при затратах 15 млн.руб. Чистая прибыль составит 80-15=65 млн.руб. Если , то мы получаем 8 млн.руб. в год в течение 2 лет и 5 млн.руб. в год в течение 8 лет. Чистая прибыль составит 16+40-15=41 млн.руб. Если 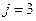, то мы получаем 5 млн.руб. в год в течение 2 лет и 8 млн.руб. в год в течение 8 лет. Чистая прибыль составит 10+64-15=59 млн.руб. Если , то мы получаем 5 млн.руб. в год в течение 10 лет. Чистая прибыль составит 40-15=25 млн.руб. Закон распределения случайной величины дохода определяется таблицей


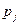
	0.42	0.18	0.28	0.12

Средний доход равен

Рассмотрим случай (строим малое предприятие с последующим расширением). Если 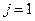, то мы получаем 8 млн.руб. в год в течение первых 2 лет и 11 млн.руб. в год в течение последующих 8 лет при затратах 15+44=59 млн.руб. Чистая прибыль составит 16+88-59=45 млн.руб. Если , то мы получаем 8 млн.руб. в год в течение 2 лет и также 8 млн.руб. в год в течение 8 лет. Чистая прибыль составит 16+64-59=21 млн.руб. Если 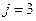, то мы получаем 5 млн.руб. в год в течение 2 лет и 11 млн.руб. в год в течение 8 лет. Чистая прибыль составит 16+66-59=23 млн.руб. Если , то мы получаем 5 млн.руб. в год в течение 2 лет и 8 млн.руб. в год в течение 8 лет. Чистая прибыль составит 10+64-59=15 млн.руб. Закон распределения случайной величины дохода определяется таблицей


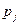
	0.42	0.18	0.28	0.12

Средний доход равен

Вывод: среднее значение прибыли выше для решения №2, то есть разумно строить малое предприятие без расширения.

Следующая задача относится к ситуации, когда ЛПР знает матрицу последствий, но распределение вероятностей на множестве возможных ситуаций не известно. Есть несколько возможных разумных способов выбирать решение в данном случае. Опишем три таких способа.

Правило Вальда максимального пессимизма. Мы ожидаем, что “природа играет против нас”, и, какое бы решение мы не приняли, будет реализована ситуация, приносящая нам наименьшую выгоду. Тогда ЛПР должно для каждой стратегии выбрать минимальное значение из чисел

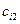, , ¼, ,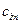

а затем выбрать ту стратегию , для которой этот минимум наибольший. Следовательно, руководствуясь правилом Вальда, ЛПР выберет максиминную стратегию, которая гарантирует ему максимально возможный выигрыш

в самой неблагоприятной для него ситуации. Этот выбор гарантирует, что ЛПР получит прибыль не меньше , независимо от того, какя ситуация сложится.

Правило Сэвиджа минимального риска. Это правило основано на понятии риска, понимаемого в данном случае как недополученная выгода. Именно, предположим, что в будущем сложится ситуация номер 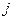. Если ЛПР заранее знает об этом, он выберет ту стратегию , для которой значение максимально среди всех элементов матрицы последствий в 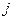–м столбце

Назовем риском –й стратегии при условии реализации 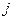–й ситуации величину

Рассмотрим матрицу рисков

Естественно, ЛПР должен вбырать ту стратегию, риск которой (потеря прибыли по сравнению с максимально возможным значением этой прибыли в той ситуации, которая сложится в будущем) минимален. Будем считать, что природа, по-прежнему, играет против нас, и она значет, какую стратегию выбрал ЛПР. Тогда для любой выбранной стратегии природа позабодится о том, чтобы выпала ситуация, дающая максимальный риск, то есть выберет , для которого

В таком случае, ЛПР должно заранее выбрать стратегию , для которой реализуется минимум среди этих максимумов. Следовательно, оптимальным поведением ЛПР является минимаксная стратегия в игре с платежной матрицей . Его риск при этом окажется не больше

независимо от того, какая ситуация реализуется в будущем.

Правило Гурвица. В этом случае ЛПР при выборе своей стратегии руководствуется смешанным критерием

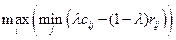в котором число выбирается произвольно и отражает, насколько важны для ЛПР возможность получить наибольшую гарантированную прибыль, с одной стороны, и обеспечить наименьшие возможные потери по сравнению с максимально возможной прибылью, с другой стороны. Например, если оба критерия равноценны для ЛПР, то он должен положить , сформировать матрицу , и найти свою максиминную стратегию в игре с такой платежной матрицей. 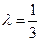Если риск операции в два раза важнее гарантированной прибыли, то , и следут положить , сформировать платежную матрицу , и найти максиминную стратегию в этом случае. В общем случае, если ЛПР решает, что для него соотношение “риск : гарантироанный выигрыш” равно , то он решает уравнение , формирует платежную матрицу 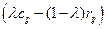, а заетм находит свою максиминную стратегию в предположении, что его противник заранее знает об этом выборе.

Задача 9.2. У лица, принимающего решение, имеется 4 возможных способа действий. Следствием каждого такого решения является доход, который получит фирма в зависимости от будущей рыночной ситуации. Всего возможно пять различных ситуаций: 1 – чрезвычайно благоприятная, 2 - благоприятная, 3 – нейтральная, 4 – неблагоприятная, 5 – крайне неблагоприятная. Известна матрица последствий для каждого из принятых решений в каждой из возможных ситуаций.

Номер решения	Ситуация
I	II	III	IV	V
					-11
					-9
					-4
					-4

Определить выбор решения, исходя из правила Вальда максимального пессимизма. Определить матрицу рисков. Найти оптимальное поведение ЛПР, исходя из правила Сэвиджа минимального риска. Определить поведение ЛПР, исходя из критерия Гурвица (рассмотреть комбинированный функционал с равными весами). Считая все возможные рыночные ситуации равновероятными, определить решение ЛПР, исходя из правила Лапласа максимизации среднего ожидаемого дохода.

Решение. Матрица последствий имеет вид

Руководствуясь правилом Вальда, подчеркнем в каждой строке наименьшее число.

Найибольшее среди них равно и достигается либо при , либо при . Таким образом, правило Вальда предписывает выбрать либо третью, либо четвертую стратегию.

Сформируем матрицу рисков. Для этого сначала в каждом столбце найдем наибольшее число.

Теперь вместо каждого из элементов матрицы последствий напишем разность подчеркнутого числа в 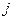–м столбце и самого элемента :

Матрица рисков найдена. Чтобы воспользовться правилом Сэвиджа, подчеркнем в каждой строке наибольший элемент.

Наименьшим среди подчеркнутых чисел является число 4 и стоит оно в четвертой строке. Следовательно, правило Сэвиджа предписывает ЛПР выбрать стратегию №4.

Воспользуемся правилом Гурвица с весовыми коэффициентами 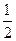, 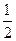. Для этого сформируем матрицу

Теперь найдем максиминную стратегию в игре с найденной матрицей. Для этого в каждой строке найдем наименьший элемент.

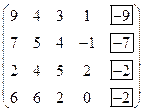
Максимум из этих числе равен 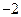и достигается при или . Следовательно, критерий Гурвица советует выбрать либо третью, либо четвертую стратегию.

Используем теперь критерий Лапласа. Будем считать, что каждая из 5 возможных рыночных ситуаций равновероятна, и появляется, следовательно, с вероятностью . Тогда для любой выбранной стратегии прибыль становится случайной величиной. Найдем распределения этой случайной величины при и ее среднее значение в каждом случае. При имеем

					-11

Аналогично, при

при

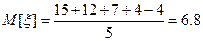
Следовательно, наибольшее среднее значение прибыли достигает при выборе стратегии №3.

В заключение, рассмотрим подход к выработке оптимального решения, основанный на понятии марковской цепи. Предположим, что система в моменты времени может находиться в одном из состояний. Состояние системы в момент времени определяется ее состоянием в момент времени следующим образом: вероятность перехода из состяния 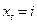в состояние 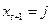не зависит от и равна . Таким образом, имеется матрица вероятностей перехода из состояния в состояние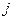

Отметим, что сумма элементов каждой строки матрицы равна 1:

, .

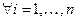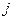Теперь представим себе, что у ЛПР имеется некоторый набор стратегий , выбор которых влияет на вероятность перехода системы из одного состояния в другое и, следовательно, каждой из которых отвечает некторая матрица вероятностей перехода . Известно, что в том случае, когда осуществляется переход системы из –го состояния в –е под воздествием –й стратегии, ЛПР получает прибыль в размере . 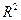Таким образом имеется матриц прибыли , , ¼, . Задача состоит в том, чтобы в каждый момент времени определить стратегию ЛПР , которая зависит от состояния системы на –м шаге, и которая гаранитровала бы максимальную среднюю суммарнюю прибыль ЛПР по итогам всех этапов. Пусть 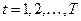, 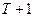. Если обозначить через максимальную среднюю суммарную прибыль ЛПР от этапов 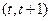, , ¼, , при условии, что в момент времени система находится в состоянии , то справедливо уравнение Беллмана

, ,

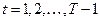То значение индекса , для которого реализуется этот максимум, и есть, очевидно, номер оптимальной стратегии . Покажем, как можно решить уравнение Беллмана, на примере следующей задачи.

Задача 9.3. Фирма может рекламировать свою продукцию с помощью одного из трех средств массовой информации: радио, телевидения или газеты. Недельные затраты на рекламу с помощью этих средств оцениваются в 800, 1600 и 1200 тысяч рублей соответственно. Объем сбыта фирмы оценивается как удовлетворительный (1), хороший (2) и отличный (3). Ниже указаны переходные вероятности из одного состояния в другое при использовании каждого из трех средств массовой информации.

Радио Телевидение Газеты

Соответствующие недельные доходы (в тыс.руб.) равны:

радио- , телевидение- , газеты- . Найти оптимальную стратегию для рекламы для каждой из последующих трех недель.

Решение. У нас имеется три возможные стратегии, для которых матрицы вероятностей перехода равны

Матрицы прибыли равны соответственно

, , .

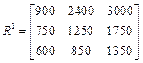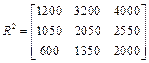Процесс выбора решения – трехшаговый. Начнем с последнего этапа (выбор стратегии для последней, третьей, недели) и определим функцию , , - максимальную среднюю прибыль, получаемую на третьей недели при условии, что объем сбыта в начале этой неделеи равен . Определим также функцию - номер стратегии, при которой достигается максимум .

Пусть сначала . Тогда для первой стратегии прибыль есть случайная величина со средним значением

900×0.4+2400×0.5+3000×0.1-800=1060;

для второй стратегии среднее значение прибыли равно

1200×0.4+3200×0.5+4000×0.1-1600=880;

для третьей стратегии среднее значение прибыли равно

1500×0.4+4000×0.5+5000×0.1-1200=1900.

Максимум достигается при выборе третьей стратегии, поэтому , .

Рассмотрим случай . Тогда для первой стратегии имеем среднюю прибыль

750×0.1+1250×0.7+1750×0.2-800=500;

для второй

1050×0.1+2050×0.7+2550×0.2-1600=450;

для третьей

130×0.1+2850×0.7+3100×0.2-1200=1550.

Следовательно, , .

Рассмотрим состояние . Тогда средняя прибыль для первой стратегии равна

600×0.1+850×0.2+1350×0.7-800=375;

для второй

600×0.1+1350×0.2+2000×0.7-1600=130

для третьей

450×0.1+1350×0.2+1600×0.7-1200=235.

Следовательно, , .

Определим теперь функцию 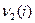максимальнюю суммарную среднюю прибыль за вторую и третью неделю при условии, что к началу второй неделеи спрос находился в состянии , , а также номер стратегии , при которой этот максимум достигается.

Пусть . Для первой стратегии имеем

(900+ )×0.4+(2400+ )×0.5+(3000+ )×0.1-800=

(900+1900)0.4+(2400+1550)0.5+(3000+375)0.1-800=2632.5;

для второй стратегии

(1200+ )×0.4+(3200+ )×0.5+(4000+ )×0.1-1600=

(1200+1900)0.4+(3200+1550)0.5+(4000+375)0.1-1600=2452.5;

для третьей стратегии

(1500+ )×0.4+(4000+ )×0.5+(5000+ )×0.1-1200=

(1500+1900)0.4+(4000+1550)0.5+(5000+375)0.1-1200=3472.5.

Таким образом, , .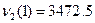

Предположим, что к началу второй недели спрос находится в состоянии . Тогда для первой стратегии среднее значение прибыли за вторую и третью неделю будет равно

(750+ )×0.1+(1250+ )×0.7+(1750+ )×0.2-800=

(750+1900)×0.1+(1250+1550)×0.7+(1750+375)×0.2-800=1850;

для второй стратегии

(1050+ )×0.1+(2050+ )×0.7+(2550+ )×0.2-1600=

(1050+1900)×0.1+(2050+1550)×0.7+(2550+375)×0.2-1600=1800;

для третьей стратегии

(130+ )×0.1+(2850+ )×0.7+(3100+ )×0.2-1200=

(130+1900)×0.1+(2850+1550)×0.7+(3100+375)×0.2-1200=2778.

Таким образом, , .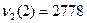

Рассмотрим случай . Для первой стратегии получаем

(600+ )×0.1+(850+ )×0.2+(1350+ )×0.7-800=

(600+1900)×0.1+(850+1550)×0.2+(1350+375)×0.7-800=1137.5;

для второй

(600+ )×0.1+(1350+ )×0.2+(2000+ )×0.7-1600=

(600+1900)0.1+(1350+1550)0.2+(2000+375)0.7-1600=892.5;

для третьей

(450+ )×0.1+(1350+ )×0.2+(1600+ )×0.7-1200=

(450+1900)0.1+(1350+1550)0.2+(1600+375)0.7-1200=997.5.

Следовательно, , .

Остается определить оптимальную стратегию для первой недели. Пусть сначала .Для первой стратегии имеем

(900+ )×0.4+(2400+ )×0.5+(3000+ )×0.1-800=

(900+3472.5)0.4+(2400+2778)0.5+(3000+1137.5)0.1-800=

=3951.75;

для второй стратегии

(1200+ )×0.4+(3200+ )×0.5+(4000+ )×0.1-1600=

(1200+3472.5)0.4+(3200+2778)0.5+(4000+1137.5)0.1-1600=

=3771.75;

для третьей стратегии

(1500+ )×0.4+(4000+ )×0.5+(5000+ )×0.1-1200=

(1500+3472.5)0.4+(4000+2778)0.5+(5000+1137.5)0.1-1200=

=4791.75.

Таким образом, , .

Предположим, что к началу первой недели спрос находится в состоянии . Тогда для первой стратегии среднее значение прибыли за вторую и третью неделю будет равно

(750+ )×0.1+(1250+ )×0.7+(1750+ )×0.2-800=

(750+3472.5)×0.1+(1250+2778)×0.7+(1750+1137.5)×0.2-800=

=3019.35;

для второй стратегии

(1050+ )×0.1+(2050+ )×0.7+(2550+ )×0.2-1600=

(1050+3472.5)×0.1+(2050+2778)×0.7+(2550+1137.5)×0.2-1600=

=2969.35;

для третьей стратегии

(130+ )×0.1+(2850+ )×0.7+(3100+ )×0.2-1200=

(130+3472.5)×0.1+(2850+2778)×0.7+(3100+1137.5)×0.2-1200=

=3947.35.

Таким образом, , .

Рассмотрим случай . Для первой стратегии получаем

(600+ )×0.1+(850+ )×0.2+(1350+ )×0.7-800=

(600+3472.5)×0.1+(850+2778)×0.2+(1350+1137.5)×0.7-800=

=2074.1;

для второй

(600+ )×0.1+(1350+ )×0.2+(2000+ )×0.7-1600=

(600+3472.5)0.1+(1350+2778)0.2+(2000+1137.5)0.7-1600=

=1829.1;

для третьей

(450+ )×0.1+(1350+ )×0.2+(1600+ )×0.7-1200=

(450+3472.5)0.1+(1350+2778)0.2+(1600+1137.5)0.7-1200=

=1934.1.

Следовательно, , .

Вывод: оптимальная стратегия не зависит от номера недели; если спрос удовлетворительный или хороший, то следует размещать рекламу в газетах; если спрос отличный, то надо воспользоваться рекламой на радио. При такой стратегии средний доход от рекламной компании составит 2074.1 тыс.руб.