Железнодорожные закругления
10.3.1. Виды и назначение железнодорожных кривых
Прямолинейные отрезки пути сопрягаются кривыми постоянного и переменного радиуса. Кривые постоянного радиуса называются круговыми, переменного – переходными. На железных дорогах используют круговые кривые с радиусами 200...4000 м и переходные кривые длиной 20...200 м.
При переходе состава с прямой на круговую кривую скачком появляется центробежная сила, вызывающая удар колес о наружный рельс. Для смягчения перехода круговую кривую сопрягают с прямой переходной кривой, радиус кривизны которой меняется от бесконечности до радиуса кривизны круговой кривой, чем обеспечивается постепенное нарастание центробежной силы и плавность движения состава. В качестве переходных кривых используют отрезки радиоидальной спирали – клотоиды.
На железных дорогах России практически все кривые составные, т.е. состоят из круговой и двух переходных кривых.
Для выравнивания давления колёс на рельсы в пределах переходной кривой устраивают возвышение наружного рельса по отношению к внутреннему (выполняют «отвод возвышения») на величину h, зависящую от скорости движения. На железных дорогах России применяют возвышение в пределах 150 мм, а уклон отвода возвышения 1‰, т.е. возвышение изменяется на 1 см на каждые 10 м длины переходной кривой.
На рис. 10.1 показан план пути в кривой, а на рис. 10.2 – профиль рельсов в железнодорожной кривой.
| НПК НКК НКК – начало круговой кривой, l НПК – начало r = ¥ переходной кривой, КПК КПК – конец K переходной кривой, r = Rl – переходная кривая, К – круговая кривая Рис. 10.1 |
| наружный рельс КПК K КПК l1 l2 ih h i НПК НПК внутренний рельс h – возвышение, i – уклон отвода возвышения Рис. 10.2 |
10.3.2. Расчет и разбивка круговых кривых
При подходе к вершине угла поворота работы по разбивке пикетажа прекращаются, производится расчет кривой и закрепление на местности ее главных точек – начала кривой НК, середины кривой СК, конца кривой КК. Для этого определяют элементы кривой: тангенс, кривую, домер и биссектрису (рис. 10.3).
Тангенс Т – это длина касательной от вершины угла до начала кривой или конца кривой. Кривая К – длина кривой от начала кривой до конца кривой. Домер Д– разность между длиной двух тангенсов и кривой. Биссектриса Б – расстояние от вершины угла до середины кривой.
Элементы кривой вычисляются как функции двух параметров: радиуса кривой R и угла поворота q:
Т = R×tg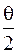 
, 
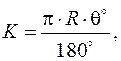Д = 2Т – К , 
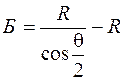. (10.1)
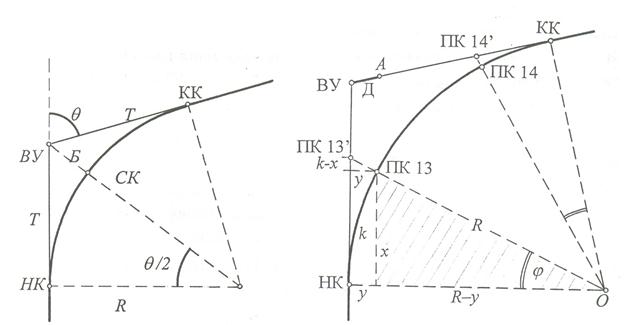
Рис. 10.3 Рис. 10.4
Все элементы кривой являются линейными функциями радиуса, их вычисляют с помощью калькулятора или выбирают из специальных таблиц (Д.И. Власов, В.Н. Логинов «Таблицы для разбивки кривых на железных дорогах») с точностью 1 см.
Вычислив элементы кривой, вставляют кривую в пикетаж, т.е. вычисляют пикетажное положение главных точек кривой по формулам:
ПК НК = ПК ВУ – Т; ПК КК = ПК НК + К; ПК СК = ПК НК + 0,5К; (10.2)
контроль: ПК КК = ПК ВУ + Т - Д ; ПК СК = ПК ВУ - 0,5Д . (10.3)
Точность пикетажных расчетов 1 см.
Пример: R = 300 ; ВУ ПК 13 + 52,05 ; Т = 81,00 ; К = 158,23 ; Д = 3,77 ;
По формулам (10.2) находим:
НК = 1352,05 – 81,00 = 1271,05 Þ ПК 12 + 71,05 ;
КК = 1271,05 + 158,23 = 1429,28 Þ ПК 14 + 29,28 ;
СК = 1271,05 + 79,12 = 1350,17 Þ ПК 13 + 50,17 ;
Контроль по формулам (10.3):
КК = 1352,05 + 81,00 – 3,77 = 1429,28 Þ ПК 14 + 29,28 ;
СК = 1352,05 – 1,88 = 1350,17 Þ ПК 13 + 50,17 .
Для закрепления на местности главных точек кривой:
· от вершины угла в обе стороны по трассе откладывают значение Т и закрепляют кольями точки НК и КК;
· разделив теодолитом пополам внутренний угол, по направлению биссектрисы откладывают значение Б и закрепляют точку СК.
Главные точки кривой закрепляют как пикеты, на сторожках подписывают их пикетажное положение.
10.3.3. Перенос пикетов с тангенса на кривую, учет домера
при разбивке пикетажа
Если между НК и ВУ попадают пикеты, то при разбивке кривой их переносят с тангенса на кривую. Расчет элементов переноса выполняют в прямоугольной системе координат, начало которой помещают в точку НК, а ось Х совмещают с направлением тангенса Т (рис. 10.4). Прямоугольные координаты пикета определяют по формулам
x = Rsinj ,
y = R – Rcosj , (10.4)
j = k/R , радиан,
где k – длина кривой от НК до пикета.
В приведенном выше примере между точками НК и ВУ попадает ПК 13, расстояние до которого от начала кривой k = ПК 13 – ПК НК = 28,95 м.
Установив на калькуляторе переключатель в положение RAD, по формулам (10.4) получим:
j = 28,95/300 = 0,0965 ; х = 28,91 ; у = 1,40 .
Одновременно вычисляют «кривую без абсциссы» – отрезок (k – х)= 0,04 м.
Вместо калькулятора можно использовать указанные ранее таблицы.
Вычислив элементы переноса, от предварительно закрепленной на тангенсе точки ПК 13¢ в сторону точки НК откладывают отрезок (k – х), в полученной точке с помощью экера восстанавливают перпендикуляр к тангенсу, по направлению которого откладывают ординату у и закрепляют ПК 13 на кривой. Предварительно закрепленную на тангенсе точку ПК 13¢ убирают.
При продолжении разбивки пикетажа от вершины угла нужно учесть домер. Измерение линий ведут по касательным, т.е. по тангенсам, а счет расстояний ведут по кривой, которая короче двух тангенсов на величину домера. Вычислив элементы кривой, величину домера откладывают от вершины угла впереди продолжают измерения от полученной точки (точка А на рис. 10.4), считая ее пикетажное положение таким же, как у вершины угла.
Если между точками ВУ и КК попадают пикеты, то их переносят на кривую тем же способом, рассчитывая элементы переноса по формулам (10.4). Начало прямоугольной системы координат помещают в точку КК.
В приведенном примере между ВУ и КК попадает ПК 14, для которого
k = ПК КК – ПК 14 = 29,28 ; j = 29,28/300 = 0,0976 ; х = 29,23 ; у = 1,43 .
После этого продолжают разбивку пикетажа до следующей вершины угла поворота трассы.
10.3.4.Расчет и разбивка круговой кривой с двумя переходными
кривыми
В каждой точке переодной кривой выполняется условие rs = C,
где r– радиус переходной кривой в данной точке, s – длина переходной кривой от начала до данной точки, С – постоянная величина, называемая параметром переходной кривой.
В конце переходной кривой (рис.10.1) параметрС = Rl, где l – полная длина переходной кривой.
Вставка переходных кривых приводит к удлинению кривой, изменению положения точек начала, середины и конца кривой. Последовательность вставки переходных кривых показана на рис. 10.5:
· назначают длину переходной кривой l ;
· круговую кривую с обеих сторон уменьшают на половину переходной кривой l/2 ;
· оставшуюся часть круговой кривой (K – l) сдвигают к центру кривизны на величину приращения биссектрисы Бр , называемую центральной сдвижкой;
· для сохранения величины радиуса круговой кривой центр ее сдвигают из точки О в точку О¢ на величину Бр; за счет этого тангенс увеличивается на величину Тр – приращение тангенса;
· с двух сторон вписывают по полной переходной кривой, за счет чего тангенс кривой еще удлиняется на величину m » l/2 ;
· вычисляют суммированные элементы кривой:
Тс = Т + Тр + m ; Kс = K + l ; Бс = Б + Бр ;
Дс = 2Тс – Кс =2T+2Tр+2m–K–l = (2Т – К) +2Тр – 2(l/2 – m) = Д + Др ,
где Др = 2Тр – 2(l/2 – m) » 2Tp – 0,02 ;
· вычисляют пикетажное положение главных точек кривой :
ПК НК = ПК ВУ –Тс ; ПК КК = ПК НК+Кс ; ПК СК = ПК НК+0,5Кс ;
контроль: ПК КК = ПК ВУ + Тс – Дс ; ПК СК = ПК ВУ – 0,5Дс .
Величина р называется сдвижкой круговой кривой относительно линии тангенса. Элементы переходной кривой: Тр , m , Бр – выбирают из тех же таблиц для разбивки кривых по длине переходной кривой l.
Рис.10.5
Разбивку составных кривых на местности производят аналогично разбивке круговой кривой, используя суммированные элементы.