Основы теории представлений в квантовой механике. Линейные вектора и операторы квантовой механики.
Математический аппарат и аксиоматика
Квантовой механики.
Основы теории представлений в квантовой механике. Линейные вектора и операторы квантовой механики.
Дифференциальные уравнения, полученные нами в предыдущих разделах, представляют собой частный случай линейных операторов, а функции 
– частный случай векторов, на которые действуют эти операторы. Алгебра многомерных векторов – тот математический аппарат, на языке которого даётся общая формулировка квантово-механических законов. Для простоты изложения начнём с хорошо известных векторов трёхмерного пространства.
3.2.1.1.а. Пространство состояний квантово-механической системы. Векторы состояния в линейном гильбертовом пространстве состояний.
Трёхмерный вектор 
однозначно задаётся тройкой компонент (проекций) вектора на три неэквивалентных направления в пространстве: 
, 
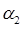и 
. Сумма двух векторов в пространстве и 
– есть новый вектор, составленный из сумм одноимённых компонент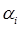 
и 
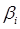, тогда соответственно:
таким образом:
Умножение вектора на скаляр (число) 
, есть «растяжение» вектора в раз и отвечает новому вектору вида:
Для пары действительных векторов и вводится числовая характеристика – скалярное произведение. При скалярном перемножении двух векторов получают скаляр (число):
равное сумме произведений их проекци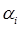й и 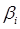. Модулем (длиной) вектора называют выражение вида:
здесь:
Во многих задачах неизбежен переход от вещественных (действительных) чисел к комплексным. Так некоторое число вида:
где 
– любые действительные (вещественные) числа и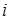 
– мнимая единица:
называется комплексным числом, где 
действительная часть комплексного числа 
, а 
- мнимая часть комплексного числа . Если изобразить комплексное число в виде: 
, что отразится точкой на плоскости oxy, то абсциссой данной точки будет служить действительная, а ординатой – мнимая части комплексного числа . Поэтому ось абсцисс ox называется действительной осью, а ось ординат oy – мнимой осью; плоскость же называется комплексной плоскостью. Положение точки на комплексной плоскости задаётся радиус-вектором 
, идущим из начала координат в указанную точку местонахождения рассматриваемого комплексного числа. Проекциями вектора на оси абсцисс и ординат являются соответственно действительная и мнимая части комплексного числа , тогда очевидно: при y=0, комплексное число есть действительная величина, изображаемая точкой на действительной оси, т.е.
Если же x=0, то комплексное число в таком случае будет представлять собой мнимую величину, которой соответствует точка на мнимой оси, т.е.
В теории комплексных чисел вводят понятие комплексного сопряжения, т.е. каждому комплексному числу , ставится в соответствие комплексно сопряжённая ему величина 
, тогда, следовательно:
здесь:
поскольку:
тогда будем иметь соответственно:
учитывая, что:
следовательно:
таким образом:
поскольку:
поэтому:
и аналогично:
таким образом, в ходе проделанных выкладок приходим к выражениям вида:
откуда следует, что:
На основании приведенных выше выкладок, не отрицательность скалярного квадрата:
будет выполняться, очевидно, если приведенное выше выражение будет вычисляться по более общей формуле:
тогда:
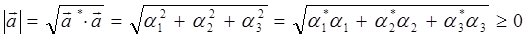
Подобным же образом уточняется скалярное произведение двух других
векторов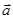 
и 
:
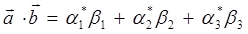
При работе с векторами в квантовой механике широко используются скобочные обозначения Дирака – так называемые «бра» и «кет» вектора. Математически они компактны, удобны в обращении и легко запоминаются.
Векторы-столбцы (кет-векторы):
тогда:
Векторы-строки (бра-векторы):
тогда:
Смысл подобной символики становится понятным после записи скалярного произведения векторов 
. Пользуясь известным из теории матриц правилом умножения строки на столбец, согласно которому: «Операция умножения двух матриц имеет место только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы». Поскольку в нашем случае число столбцов бра-вектора 
равно числу столбцов кет-вектора 
, легко получить выражение для скалярного произведения соответствующих векторов, записанные в терминах скобочных обозначений Дирака. В результате такого рода записи получим новый вектор «бракет» будем иметь соответственно:
Для упрощения и большей наглядности, изменим обозначения матричных элементов (проекций векторов) соответствующих матриц, тогда будем иметь соответственно:
произведение, представленное полной скобкой Дирака «бра-кет», составленное из матричных элементов (проекций разложения соответствующих векторов) будет имеющее вид:
будет определяться, таким образом, как скалярное произведение бра-вектора на кет-вектор . В ряде случаев удобно разложить вектор характеризующий поле действительных (вещественных) чисел по базисному набору простейших (элементарных) векторов 
, геометрическим образом которых являются декартовые единичные векторы – орты. Разложим кет-вектор по-базисному
набору простейших (элементарных) векторов:
обозначив простейшие (базисные) вектора через , будем иметь соответственно:
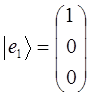
тогда, следовательно:
Полученное выше последнее выражение представляет собой разложение кет вектора по-базисному набору векторов: 
, 
, 
. Каждый такой простейший (базисный) вектор нормирован и ортогонален или говоря об одновременной его нормированности и ортогональности, говорят, что он обладает свойством ортонормированности по-отношению ко всем другим векторам из рассматриваемого базисного набора, т.е.
или, что то же самое:
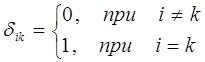
где 
символ Кронекера. Ортогональность векторов означает их линейную независимость, т.е. что векторы располагаются по-отношению друг ко другу под углом 900 и ни один из векторов данного набора нельзя выразить через линейную комбинацию остальных 
векторов. Ортогональность волновых функций как линейных векторов – фундаментальное их свойство, следующее из более общего принципа суперпозиций. Линейная независимость векторов означает, что ни один из векторов рассматриваемого векторного пространства не сводится один к другому, и, следовательно, не является линейной комбинацией других векторов из данного базисного набора, не содержит в себе примеси любого другого из векторов. Учитывая, что норма вектора есть характеристика его длины, т.е.
а также, что:
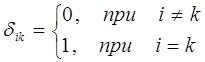
и кет-вектор соответствует волновой функции 
или 
, тогда свойство нормированности волновой функции можно интерпретировать как плотность вероятности микрочастицы, положение плотности, вероятности которой задаётся вектором , тогда соответственно будем иметь:
В различных задачах используют не трёхмерные, а многомерные (N-мерные) вектора. N-мерным кет-вектором называется упорядоченная совокупность N-комплексных чисел 
, компонент вектора , т.е.
здесь m = 1, 2, 3, 4, … k. Множество таких многомерных векторов образую N-мерное векторное пространство 
.
Для N-мерных векторов справедливы те же линейные операции, что и для уже рассмотренных выше трёхмерных векторов:
Пространство, образуемое многомерными векторами, называется также конечномерным. Наряду с пространством кет-векторов , вводится комплексно сопряжённое ему пространство 
образуемое полем N-мерных бра-векторов :
или меняя номера матричных элементов (из соображений удобства и наглядности), имеем соответственно:
Как и в случае трёхмерных векторов, для многомерных бра-векторов имеем те же линейные операции:
или после смены нумерации:
Тогда скалярное произведение многомерных векторов и будет определяться соответственно выражением вида:
здесь: 
. Таким образом, имеем соответственно:
Используя приведенные выше рассуждения, можно сформулировать достаточно простые правила для скалярного произведения векторов и :
Многомерные векторы, как и трёхмерные, можно разложить по-базисному набору элементарных (простейших) векторов, т.е.
здесь:
Полученное таким образом выражение:
представляет собой разложение кет-вектора по-базисному набору простейших (элементарных) векторов . Базис представляет собой набор элементарных векторов, он обладает важным качеством – ортонормированностью. Это в свою очередь говорит о том, что он должен удовлетворять условиям вида:
таким образом, имеем:
Данное утверждение удобней записывать, используя символ Кронекера 
:
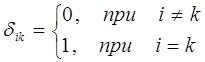
тогда соответственно:
Всякий базис удовлетворяющий данным условиям, называется ортонормированным. В ортонормированном базисе, коэффициенты разложения вычисляются как скалярное произведение:
Таким образом, для случая многомерных векторов образующих конечномерное векторное пространство , будем иметь:
Умножая правую и левую части полученного выражения на базисный вектор вида и учитывая условия вида:
имеем соответственно:
здесь:
Таким образом, для коэффициентов разложения (называемых также коэффициентами Фурье) приходим к выражению вида:
Выражая разложение по-базисному набору векторов через соответствующие коэффициенты Фурье , имеем соответственно:
т.к. 
, тогда, следовательно:
Отсюда следует, что если система векторов ортонормирована, то она служит базисом Ω векторного пространства состояний. Покажем теперь, что множество функций можно воспринимать как векторное пространство бесконечного числа измерений. Такое пространство называется в квантовой механике функциональным. В общем случае функциональное пространство – это тип векторного пространства, образованное множеством функций. Так, пусть имеется множество функций одной переменной 
на заданном интервале 
. Разобьем интервал на 
частей длиной 
, учтём также, что 
. Тогда всю совокупность действительных (вещественных) значений функции можно представить кет-вектором 
, который при 
даёт точное представление о функции и таким образом значение в точке 
оказывается одной из компонент функционального вектора . На основании представлений о функциональном пространстве и выражении функции как некоторого функционального кет-вектора :
можно уточнить представления о скалярном произведении двух векторов. Пусть у нас имеется две функции вида и 
. Рассматривая их как некоторые многомерные функциональные вектора и 
, определим их скалярное произведение. Очевидно, что при , соответствующая сумма:
Может разойтись, т.е. при безграничном возрастании , ряд 
перестаёт стремиться к какому-либо пределу. Для того чтобы данный ряд сходился, домножим правую часть данного выражения на величину - длину участка интервала разбиения 
, будем иметь соответственно:
Тогда в пределе при полученная сумма перейдёт в интеграл, который и будет представлять собой скалярное произведение функций и , тогда:
Очевидно при 
, функции и будут ортогональны и соответственно при 
- нормированы. Следуя далее такого рода соображениям, имеем:
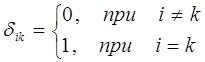
Бесконечномерность пространства функций позволяет записать аналог разложения вектора по-базису в виде некоторого бесконечного ряда:
где всей бесконечной совокупности базисных векторов 
отвечает бесконечный набор базисных функций вида: 
, 
, 
, 
, …, 
. Это в свою очередь означает, что для самой функции можно записать:
домножая правую и левую части выражения вида:
на соответствующий базисный вектор , а также с учётом того что набор базисных векторов ортонормирован, т.е. для него справедливы условия вида:
поскольку:
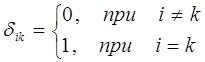
тогда соответственно:
откуда:
или в окончательном виде:
Итак, как было выяснено нами выше, состояние системы в квантовой механике полностью определяется вектором бесконечномерного пространства функций. Такой вектор называют вектором состояния, или волновой функцией, и обычно обозначают через 
. Вектор может быть задан в дискретном представлении:
где 
– бесконечный набор ортонормированных (независимых) векторов состояния. Тот же вектор, как было показано уже выше, может быть представлен в так называемом координатном представлении в виде функции 
. Тогда значение функции в точке x есть непрерывная компонента вектора , т.е.
В зависимости от выбранного представления, скалярное произведение волновой функции и некоторой другой функции 
:
может быть вычислено по одной из формул вида:
откуда:
То, что волновые функции принадлежат линейному векторному пространству Ω, есть прямое следствие общего принципа – принципа суперпозиции, справедливого для многих волновых процессов. Согласно данному принципу, если и – два допустимых вектора состояния, то и любая их линейная комбинация также будет описывать допустимое состояние той же системы.
3.2.1.1.б. Линейные операторы квантовой механики.
Необходимость преобразования векторов друг в друга приводит к общему понятию оператора, действующего в некотором векторном пространстве . Оператором 
называется линейное отображение (операция) вида:
в ходе которого каждому многомерному вектору 
из некоторого конечномерного векторного пространства , ставится в соответствие новый вектор из того же - пространства. Это в свою очередь означает, что оператором является некоторое математическое действие (операция), позволяющее исходную функцию одного вида - оригинал, «перевести» в функцию другого вида 
- отображение. Оператор считается заданным, если указано не только правило, с помощью которого он «преобразует» одну функцию (многомерный вектор) в другую, но и, то множество функций, на которые действует данный оператор. Множество функций, на которые может действовать оператор, называется областью определения этого оператора.
Среди всех возможных операторов, известны следующие тривиальные операторы:
1. Нулевой оператор 
переводит все вектора в нуль, т.е. 
.
2. Единичный оператор 
(оператор идентичности) – умножает все вектора на единицу, не изменяя, таким образом, вектора 
.
3. Скалярный оператор 
- умножает все вектора на скаляр (число), растягивая все вектора в 
раз, т.е. 
.
4. Обратный оператор 
- определён так, что из выражения 
можно найти , т.е. что 
.
Таким образом, если по-определению оператор переводит функцию (вектор) в функцию (вектор) , то обратный оператор осуществляет обратное действие – переводит вектор в ; т.е. операторы и есть взаимообратные операции, таковыми являются, например операции: дифференцирования и интегрирования, возведение в степень и извлечение корня, умножение на число и деление на то же самое число, логарифмирование и потенцирование и т.д. Не для каждого оператора существует обратный ему оператор. Так, оператор умножения на нуль - не имеет обратного оператора, поскольку из равенства вида: , при 
следует что: 
, т.е. нельзя найти переменную . Достаточно очевидно, что обратный оператор удовлетворяет тождеству: 
. В квантовой механике используют операторы только лишь определённого класса: так называемые линейные самосопряжённые (эрмитовые) операторы. Оператор называется линейным, если выполняется условие вида:
Рассматривая функции 
и как некоторые многомерные векторы некоторого конечномерного векторного пространства , запишем свойство линейности оператора в терминах скобок Дирака:
К линейным относят операторы интегрирования и дифференцирования, а также скалярный оператор. Нелинейными являются операторы возведения в степень и извлечение корня. Самосопряжённым (эрмитовым) называется оператор, если для двух интегрируемых функций и или соответствующих им многомерных векторов 
и 
, выполняется соотношение вида:
Действительно, так как:
то очевидно выражение не изменится, если подействовать на вектор единичным оператором (идентичности) , тогда соответственно будем иметь:
поскольку:
очевидно, аналогичное выражение для комплексного сопряжения векторов и будем иметь и в случае действия на одного из них единичного оператора :
Достаточно очевидно, что выражение, полученное для единичного оператора (идентичности) может быть распространено на любой класс операторов обладающих свойством эрмитовости, поэтому:
таким образом, находим, что:
Сумма (разность) линейных операторов есть новый оператор 
, действующий на произвольный вектор , т.е.
сумма линейных эрмитовых операторов обладает свойствами коммутативности:
и ассоциативности:
Произведением двух и большего числа операторов называется оператор вида:
действующий на произвольный вектор . Действие данного оператора сводится к последовательному выполнению над вектором 
операций, где число перемножаемых между собой операторов, т.е. если 
и 
, тогда:
Очевидно, произведение двух и большего числа одинаковых операторов будет определяться выражением вида:
Произведение линейных самосопряжённых операторов обладает свойствами: ассоциативности, дистрибутивности и коммутативности:
1. Свойство ассоциативности:
2. Свойство дистрибутивности:
3. Свойство коммутативности: В общем случае действие оператора 
не совпадает с действием оператора 
, т.е. 
, поэтому свойство коммутативности для произведения операторов и не выполняется. Если же два оператора имеют одну и ту же область определения и одинаковым образом действуют на вектор , то это будет выражаться равенством вида:
и
В противном случае операторы не равны между собой, имеют различные области определения и соответственно различным образом будут действовать на одну и ту же функцию (вектор) и свойством коммутативности таким образом обладать не будут. Если же имеет место равенства вида:
тогда соответственно:
и соответствующие операторы будут коммутировать между собой. В противном случае, т.е. когда выполняется условие вида:
операторы 
и 
коммутировать между собой не будут. Выражение, заключённое в скобках:
называется коммутатором двух операторов и 
. Используя понятие коммутатора 
, представим последнее выражение в виде:
Очевидно условие коммутативности, выраженное через коммутатор двух операторов , можно записать в виде:
и соответственно:
В первом случае, при 
, операторы будут коммутировать, в противном случае, при 
, операторы коммутировать не будут. Сформулируем теперь основные свойства коммутаторов:
Основываясь на свойствах коммутаторов, решают задачу об одновременной измеримости двух динамических переменных (физических величин) в квантовой механике. Действительно, пусть у нас имеется две взаимосвязанные динамические переменные (физические величины), которым отвечают соответствующие им квантово-механические операторы и 
. При этом каждому из операторов соответствует свой набор собственных значений физической величины, которой в квантовой механике ставится в соответствие линейный самосопряжённый оператор. В квантовой механике взаимосвязь между операторами и динамическими переменными (физическими величинами) – оригиналами и их отображениями, выражается соответствующими операторными уравнениями вида:
тогда соответственно:
Для решения принципиального вопроса касающегося одновременной измеримости двух взаимосвязанных физических величин (динамических переменных), составим соответствующее этим операторам коммутационное соотношение. При этом если данные операторы будут коммутировать между собой, т.е. если 
, то имеется отличная от нуля возможность одновременного измерения соответствующих этим операторам динамических переменных. Отличие же коммутаторов от нуля, т.е. если 
, указывает на то, что совместное измерение двух динамических переменных (физических величин) в квантовой механике невозможно (операторы не коммутируют между собой), имеем соответственно:
таким образом:
Это в свою очередь находится в полном соответствии с принципом неопределённости В. Гейзенберга, отрицающий возможность одновременного измерения двух динамических переменных (физических величин). Тогда система уравнений вида:
будет представлять собой математическое выражение принципа неопределённости В. Гейзенберга, сформулированного на языке операторов квантовой механики.
3.2.1.1.в. Задача на собственные значения оператора.
Задачей на собственные значения оператора, называют операторное уравнение вида:
здесь - линейный самосопряжённый (эрмитовый) оператор; - собственные функции оператора; 
- собственные значения оператора, которые представляют собой допустимые значения динамической переменной (физической величины), которой ставится в соответствие линейный самосопряжённый (эрмитовый) оператор. Поэтому указанное выше операторное уравнение может быть переписано соответственно в виде:
Решить задачу на собственные значения оператора, означает найти такой набор функций 
, которые «растягиваются» в 
- раз (умножаются в - раз) под действием данного оператора . Неизвестными в данной задаче являются как собственные функции , так и собственные значения (числа) 
. Если решение задачи на собственные значения оператора даёт 
- значений и эти собственные значения оператора оказываются одинаковыми, то говорят о вырождении, т.е.
При этом собственные значения, а также соответствующие им собственные функции называют - кратно вырожденными. Приведём ряд важных теорем (опуская их доказательства, выходящие за рамки данной работы), в которых отражены свойства задачи на собственные значения.
Th.1: «Если оператор эрмитов, то все его собственные значения являются действительными числами».
Th.2: «Если оператор эрмитов, а собственные значения этого оператора 
и 
различны, то соответствующие собственные функции (векторы) 
и взаимно ортогональны», т.е. имеем:
Th.3: «Система собственных функций (векторов) 
эрмитова оператора полна, т.е. любую функцию 
, принадлежащую тому же пространству, что и набор собственных функций оператора можно представить в виде суммы:
поскольку:
=
здесь 
- некоторые действительные (вещественные) числа, определяемые как коэффициенты Фурье».
Th.4: «Если несколько собственных функций (векторов) принадлежит одинаковым собственным значениям (случай вырождения), то любая их линейная комбинация является решением той же задачи на собственное значение с тем же собственным значением».
Th.5: «Если система собственных функций (векторов) оператора является в то же время и системой собственных функций оператора , то оператора и коммутируют».
Th.6: «Если операторы и коммутируют, то они имеют общую систему собственных функций».
3.2.1.1.г. Матричное представление оператора.
Чтобы полностью задать оператор, необходимо указать явно правило преобразования данным оператором каждого вектора из Ω пространства. Другой путь состоит в задании правил преобразования только базисных векторов 
. Так, пусть оператор 
переводит вектор 
в вектор 
, т.е. имеем:
Рассмотрим представление векторов и в виде разложения по некоторому ортонормированному базису , 
, где 
– число базисных векторов:
Выясним теперь, как можно использовать ортонормированный базис для представления операторов. С учётом свойств линейности и эрмитовости операторов квантовой механики, а также учитывая разложение соответствующих векторов и по некоторому ортонормированному базису, запишем:
или в общем виде:
Из полученного выражения следует, что действие оператора на вектор сводится к действию этого оператора на базисные векторы :
Необходимо отметить, что коэффициенты разложения 
и 
являются скалярными величинами и, следовательно, в алгебраических выражениях их можно менять местами с векторами, т.е. 
и 
. Рассмотрим детально структуру оператора в базисе векторов . Для этого умножим уравнение:
слева на каждый из бра-векторов 
, где , где – число базисных векторов. В результате получим:
Раскрывая скобки в полученном выражении, будем иметь соответственно:
или в общем виде, с учётом ортонормированности базиса:
Действительно, учитывая, что:
а также:
имеем:
откуда, с учётом ортонормированности базиса:
и таким образом:
Умножая уравнение:
слева на вектор 
, будем иметь соответственно:
или после раскрытия скобок:
или в общем виде, с учётом ортонормированности базиса:
Аналогичные уравнения можно получить для произвольного коэффициента 
:
или в окончательном виде:
Вводя следующие обозначения:
или в общем виде:
Коэффициенты 
называют матричными элементами оператора в базисе векторов , причём 
– диагональные и – недиагональные матричные элементы. С использованием введенных выше обозначений, полученное нами выше выражение можно будет представить далее к виду:
или
Полученное выражение, представляет собой систему линейных уравнений, записанную в самом общем виде:
Всю совокупность коэффициентов соберём в виде матрицы:
и таким образом, действие оператора на вектор :
в общем случае будет сводиться к процедуре умножения матрицы на вектор в соответствии с известным правилом – строка умножается на столбец, т.е. имеем:
При этом необходимо отметить, что если оператор, действующий на вектор в линейном гилбертовом пространстве состояний является самосопряжённым (эрмитовым), то между недиагональными матричными элементами такого оператора имеется связь 
. Так, по определению, действительно, имеем:
или в интегральной форме:
В том случае, когда матричные элементы эрмитова оператора – вещественные числа, матрица является симметричной 
. Необходимо отметить, что в квантовой механике, как правило, приходится иметь дело с симметричными матрицами операторов физических величин. В функциональных пространствах матрица оператора является бесконечномерной, и в базисе ортонормированных функций 
матричные элементы вычисляются с использованием интеграла:
Центральную проблему квантовой механики – задачу на собственные значения оператора – также можно представить в матричном виде. Так, по определению имеем соответственно операторное уравнение вида:
где 
– собственное значение, соответствующее собственным значениям волновой функции 
. На основании изложенного выше, рассмотрим представление собственной функции в виде разложения по базисным функциям 
. Так, имеем соответственно
